Неопределенный интеграл
Пример 1. Найти неопределенные интегралы:
А) 
Б) 
В) 
Решение. При нахождении данных интегралов используем формулу 
.
А) 
Б) 
В) 
Пример 2. Найти 
.
Решение. Пусть 
. Следовательно, по формуле интегрирования по частям 
:
.
Пример 3. Найти неопределенные интегралы от рациональных дробей: А) 
Б) 
Решение. А) 
.
Б) Представим дробь в виде суммы простейших дробей:
.
Отсюда следует
.
Для нахождения неопределенных коэффициентов А, В и С используем метод отдельных значений аргумента.
Положим 
, тогда 
, т.е. 
;
положим 
, тогда 
; так как , то 
;
положим 
, тогда 
, так как и , то 
. Следовательно:
.
Поэтому
Пример 4. Найти 
.
Решение
Пример 5. Найти 
.
Решение. Положим 
. Отсюда 
.
Следовательно:
Пример 6. Найти 
.
Решение 
Пример 7. Найти 
.
Решение. Положим 
, 
. Тогда
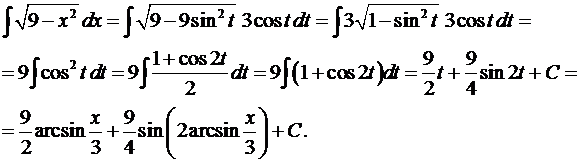
Пример выполнения типового расчета по теме
Определенный интеграл
Пример 1. Вычислить определенный интеграл 
.
Решение. Известно, что если функция 
непрерывна на отрезке 
, то она интегрируема на этом отрезке и
,
где 
- какая-нибудь первообразная для на отрезке .
Указанная формула называется формулой Ньютона-Лейбни-ца. При нахождении первообразной используются те же методы интегрирования, что и для неопределенных интегралов. Следовательно:
Пример 2. Найти 
.
Решение. Здесь подынтегральная функция 
непрерывна на
всей оси Ox. Поэтому (по определению) 
.
Вычислив интеграл 
, найдем
.
Следовательно:
(по правилу Лопиталя 
).
Таким образом, интеграл 
существует (сходится) и равен единице.
Пример 3. Найти 
.
Решение. Здесь подынтегральная функция 
обращается в бесконечность между пределами интегрирования 
.
Следовательно (по определению):
где e и s принимают положительные значения.
Эти пределы не существуют (как обычно говорят, «равны ¥»).
Таким образом, интеграл не существует (расходится).
Пример 4. Исследовать, сходится ли интеграл
.
Решение. Подынтегральная функция терпит разрыв в точке x =0. Очевидно, что при x ³0
.
Так как несобственный интеграл
,
т.е. сходится, то сходится и исходный интеграл.
Пример 5. Треугольная пластинка с основанием a =3 м и высотой H =2 м погружена вертикально вершиной вниз в жидкость так, что основание параллельно поверхности жидкости и находится на расстоянии d =1 м от поверхности. Плотность жидкости d =0,9 т/м3. Вычислить силу давления жидкости на каждую из сторон пластинки.
Решение. Для определения силы давления жидкости воспользуемся законом Паскаля, согласно которому давление Dp жидкости на площадку DS, погруженную на глубину h:
,
где d - плотность жидкости; g – ускорение свободного падения.
Рис. 1
Прямыми, параллельными поверхностям жидкости, разобьем треугольник на элементарные полоски шириной dy (рис. 1), отстоящие от поверхности жидкости на расстояние y+d. Из подобия треугольников ABC и A1B1C1 имеем
,
т.е. площадь вырезанной полоски
,
давление на каждую из сторон полоски треугольной пластины
.
Интегрируя обе части последнего равенства, получаем
.
Задачи для самостоятельного решения
Задание 1. Вычислить данные определенные интегралы.
1. 
.
2. 
.
3. 
.
4. 
.
5. 
.
Задание 2. Вычислить несобственные интегралы или установить их расходимость.
1. 
1. 
3. 
4. 
5. 
Задание 3. Решить задачи.
1. Скорость прямолинейного движения материальной точки
м/с. Найти путь, пройденный точкой от начала движения до полной остановки (Ответ: 104 м).
2. Найти момент инерции однородного стержня длиной l и
весом P относительно его конца 
3. Вычислить работу, которую необходимо затратить на со-
оружение конического кургана, радиус основания которого R=2 м, высота H=3 м, из однородного строительного материала плотностью d=2,5т/м3 (Ответ: 
кДж).
4. Вычислить силу давления воды на прямоугольник, вертикально погруженный в воду, если известно, что его основание равно 8 м, высота 12 м, верхнее основание параллельно поверхности воды и находится на глубине 5 м. Плотность воды d=1 т/м3. (Ответ: 656g»6428,8 кН).
5. Найти координаты центра масс однородной дуги цепной линии 
от точки 
до точки 
.
6. Найти координаты центра масс однородной дуги первой арки циклоиды 
, 
.
7. Найти координаты центра масс однородной плоской фигуры, ограниченной линиями 
и 
(Ответ: (1,5; 0,6)).