1. Изменения курса акций промышленной компании в течение месяца представлены в таблице:
курс акции (Дол.)
t Yt t Yt t Yt t Yt
1 509 6 515 11 517 16 510
2 507 7 520 12 524 17 516
3 508 8 519 13 526 18 518
4 509 9 512 14 519 19 524
5 518 10 511 15 514 20 521
Проверить утверждение об отсутствии тенденции в изменении курса акций двумя способами:
а) с помощью метода Фостера - Стюарта;
б) используя критерий серии, основанный на медиане выборки. Доверительную вероятность принять равной 0,95.
2. Проверим гипотезу об отсутствии тенденции в изменении курса акций с помощью критерия серий, основанного на медиане выборки.
3. Годовые данные об изменении урожайности зерновых культу; представлены в таблице. С помощью критерия "восходящих и нисходящих" серий проверить утверждение о том, что в изменении урожайности имеется тенденция.
Урожайность зерновых культур (ц/га)
| t | Yt | t | Yt | t | Yt | t | Yt |
| 6,7 | 8,6 | 8,4 | 9,1 | ||||
| 7,3 | 7,8 | 9,1 | 9,5 | ||||
| 7,6 | 7,7 | 8,3 | 10,4 | ||||
| 7,9 | 7,9 | 8,7 | 10,5 | ||||
| 7,4 | 8,2 | 8,9 | 10,2 | ||||
| 9,3 |
Доверительную вероятность принять равной 0,95.
Решение
1. Вспомогательные вычисления по методу Фостера- Стюарта представлены в таблице 1.
1) Если уровень yt больше всех предшествующих уровней, то в графе mt ставим 1, если yt меньше всех предшествующих уровней, то ставим 1 в графе lt;
2) Определяем dt=mt-1t для t=2ч20;
3) D = 
=3;
4) Значение σd для n=20 берем из таблицы 1.2.
σd =2,279.
Значение tкp берем из таблицы t- распределения Стьюдента:
tкp (а=О,05; К=19)=2,093; tH = 
= 1,316.
TH< Tkр 
нет оснований отвергнуть гипотезу об отсутствии тренда.
С вероятностью 0,95 тренд во временном ряду отсутствует.
Вспомогательные вычисления представлены в таблице 1.4.
Таблица 1
Вспомогательные вычисления по методу Фостера- Стюарта
| t | Yt | Mt | Et | Dt | t | Yt | Mt | Et | Dt |
| - | - | - -1 |
Вспомогательные вычисления представлены в таблице 2
| t | Yt | Y't | t | Yt | Y't | t | Yt | Y't | |||
| - - - - + - | + + - - + + + + | - - - + + + |
1) от исходного ряда yt переходим к ранжированному yt', расположив значения исходного ряда в порядке возрастания;
2) Т.к. n=20 (четное) 
Медиана
Ме = 
=516,5;
3) Значение каждого уровня исходного ряда yt сравнивается со значением медианы. Если yt >Ме, то δi принимает значение «+», если меньше, то «-»;
4) v (20)=8- число серий;
max (20)=4- протяженность самой большой серии.
В соответствии делаем проверку:
max (20)<[3,3(lg20+1)]
v(20)>[ 
(20+1-1.96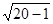 
)]
4<7
8>6
Оба неравенства выполняются. С вероятностью 0,95 тренд во временном ряду отсутствует, что согласуется с выводом, сделанным с помощью метода Фостера-Стюарта.
Таблица 3
| t | Yt | t | Yt | t | Yt | |||
| 6,7 7,3 7,6 7,9 7,4 8,6 | + + + - + | 7,8 7,7 7,9 8,2 8,4 9,1 | - - + + + + | 8,3 8,7 8,9 9,1 9,5 10,4 10,5 10,2 9,3 | - + + + + + + - - |
Вспомогательные вычисления в задании
В графе δ ставим «+», если последующее значение уровня временного ряда больше предыдущего, «-» - если меньше. Определим v (21)=8 – число серий.
max (21)=6 – протяженность самой большой серии. Табличное значение
0 (21)=5. В соответствии делаем проверку:
V(21)>[ 
]
max (21)≤ 0(21)
8>10
6≤5
Т.к. оба неравенства не выполняются, то делаем выводы: во временном ряду урожайности имеется тенденции.