II Сечение конуса
1. Секущая плоскость проходит через ось конуса (осевое сечение – равнобедренный треугольник рис. 1)
2. Секущая плоскость проходит перпендикулярно к оси конуса
- круг с центром О1 (рис. 2)
3.Сечение проходящее через верщину конуса – равнобедренный
треугольник (рис. 3)
4.Параболическое и гиперболическое сечения. (рис. 4)
В конус всегда можно вписать шар. Его центр на оси конуса
и совпадает с центром окружности, вписанно в треугольник,
являющийся осевым сечением конуса.
Rш = Rк * tg a/2 = H*Rк/Rк +L
Около конуса всегда можно описать шар. Его центр лежит на
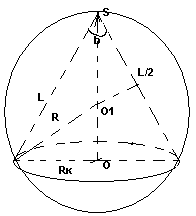оси конуса и совпадает с центром окружности, описаной около
треугольника, являющегося осевым сечением конуса.
Rш = Rк / sinb; R²ш= (H-Rш) ² + Rк²
Rш =L/2H; (2Rш - Hк)Hк = Rк²
III Площадь поверхности конуса
1. 
За плщадь боковой поверхности конуса принимается площадь её разертки. Выразим S бок через его опразующую L и радиус основания r. Площадь кругового сектора πL²/360*α. Выразим α через L и r. Длинна дуги ABA равна 2πr (длинна окружности основания конуса) 2πr = πL/180* α, откуда следует α=360r/L следовательно Sбок = πL²360r/360L=πrL
Sбок = πrL
2. Площадь полной поверхности конуса есть сумма площадей боковой поверхности и основания
Sпол=πrL(L+r)
IV Объем конуса
Объем конуса равен одной трети произведения площади основания на высоту.
Рассмотрим конус с обьемом V, радиусом R, высотой h и вершиной О. Введем ось Ох, чтобы она совпадала с осью конуса -ОН. Произвольное сечение конуса плоскостью, перпендикулярной к оси Ох, является круг с центром в точке Н1 пересечения этой плоскости с осью Ох. Обозначим Радиус этого круга через, ф площадь S(x) через,где х-абсцисса точки Н1. Из подобия треугольников ОН1А1 и ОНА следует,что ОН1/ОН=R1/R,
или x/h=R1/R =>R1=XR/h. Так как S(x)= πR², то S(x)= πR²/h²* ²
Применяя основную формулу вычисления обьемов тел при а=0 и b=h получаем
V Усеченный конус.
Усеченный конус – часть конуса, заключенная между основанием и паралельным основанию сечением конуса.
Круги с центрами О1 и О2 – верхнее и нижнее основания усеченного конуса, R r – радиусы оснований, АВ= L образующая,α угол наклона образующе и плоскости нижнего основания.
Отрезок О1О2-высота. Трапеция АВСD – осевое сечение.
Н=L*sin α
H²+(R-r) ²=L²
Около усеченного конуса всегда можно описать шар. Его центр лежит на прямой О1О2
CF=FD OF┴Cd=>
О – центр описанного шара R - радиус описанного шара, равный радиусу окружносит описанной около ΔACD
В усеченный конус можно вписать шар тогда и только тогда, когда образующая равна сумме радиусов оснований L=R+r => существует вписанный шар. 
VI Площадь поверхности усеченного конуса
1. Пусть Р – вершина конуса, из которого получен усеченный конус, АА1-одна из образующих
Усеченного конуса О и О1 – центры оснований. Используя формулу Sбок для конуса получаем
S бок = πr*PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, отсюда, учитывая, что AA1=L, находим
Sбок =πrL +π (r - r1)PA1
Выразим РА1 через L1, r и r1. Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р и поэтому PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаем PA1=Lr1/R-r1. S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1)
Sбок =πL(r+r1)
2. Площадь полной поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и оснований
Sполн = S1+S2+Sбок=πL(r+r1)+ πR²+πr²