КОНТРОЛЬНЫЕ ВОПРОСЫДЛЯ ПОДГОТОВ-
1. Дайте определение функции нескольких переменных.
| z = f (x, y) |
Если каждой паре (x, y) значений двух независимых переменных из области Wставится определенное значение z, то говорят, что z есть функция двух переменных (x, y).
2. Дайте определение предела функции нескольких пере-
менных.
Пусть функция 
определена в области 
. Число 
называется пределом функции при стремлении точки 
к точке 
, если для любой 
-окрестности точки (
) найдется такая проколотая 
-окрестность точки (
), что для всех точек из 
верно, что 
принадлежит .
Обозначение: 
.
Если предел существует, то он не зависит от того, по какому направлению точка приближается к точке .
3. Дайте определение непрерывности функции нескольких
переменных в точке.
Функция называется непрерывной в точке , если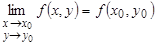 
.
Функция, непрерывная в каждой точке области, называется непрерывной в этой области.
Если в какой-то точке условие непрерывности не выполняется, эта точка называется точкой разрыва.
4. Дайте определение непрерывности функции нескольких
переменных на множестве.
Функция 
, непрерывная на замкнутом и ограниченном множестве , ограничена на этом множестве и достигает на нем своего наибольшего и наименьшего значений.
5. Дайте определение частных производных функции не-
скольких переменных.
Частной производной по переменной 
от функции в точке называется предел отношения частного приращения функции 
к приращению 
переменной при стремлении к нулю, если этот предел существует и конечен.
Обозначения: 
, 
, 
, 
.
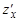Определение частной производной можно записать так:
.
Частной производной по переменной 
от функции 
в точке 
называется предел отношения частного приращения функции 
к приращению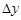 
переменной при стремлении 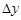к нулю, если этот предел существует и конечен.
Обозначения: 
, 
, 
, 
.
6. Сформулируйте геометрический смысл частных произ-
водных функции двух переменных.
Путь функция двух переменных 
определена на множестве и точка 
.
При вычислении частной производной 
переменная сохраняет постоянное значение 
. Функция 
задает линию пересечения поверхности с плоскостью . Из геометрического смысла производной функции одной переменной следует, что равняется угловому коэффициенту касательной к этой кривой в точке с ординатой 
или 
, где 
– угол, который эта касательная составляет с осью 
(рис.7).
Рис. 7.
Аналогично частная производная 
, где 
– угол между касательной, проведенной к пространственной кривой, заданной системой 
, в точке с координатами 
и осью 
.
7. Дайте определение дифференцируемой в точке функции
двух переменных.
Функция 
называется дифференцируемой в точке , если ее полное приращение можно представить в виде
,
где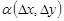 
– бесконечно малая функция более высокого порядка, чем 
при 
.
8. Сформулируйте необходимое условие дифференцируемо-
сти функции двух переменных в точке.
Если функция переменных дифференцируема в некоторой точке, то она непрерывна в этой точке и имеет в ней конечные частные производные по всем переменным, причем 
, 
.
9. Сформулируйте достаточное условие дифференцируемо-
сти функции двух переменных в точке.
Если функция имеет частные производные 
и 
в точке 
и некоторой её окрестности, и эти производные непрерывны в точке , то функция дифференцируема.
Приращения независимых переменных и 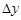называются дифференциалами переменных x и y.
Обозначение: 
.
С учётом введённых обозначений запишем формулу для полного дифференциала функции :
.
10. Дайте определение дифференциала функции двух пере-
менных.
Пусть функция определена в некоторой окрестности точки . Полным приращением функции в точке называется величина
.
Главная часть полного приращения функции называется полным дифференциалом этой функции и обозначается 
, то есть
.
11. Напишите формулу дифференциала функции двух пере-
менных.
См выше
12. Дайте определение производных второго порядка функ-
ции двух переменных.
Если существует и конечен предел 
, то он называется частной производной второго порядка от 
по дважды в точке и обозначается 
или 
.
Аналогично даются определения для остальных частных производных второго порядка.
Обозначения:
, 
, 
, 
.
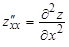13. Дайте определение стационарной точки функции двух пе-
ременных.
Точки, в которых частные производные равны нулю называются стационарными точками функции.
14. Дайте определение критической точки функции двух пе-
ременных.
В стационарных точках наличие экстремума не обязательно. Однако согласно необходимым условиям экстремума лишь в этих точках функция может достичь экстремума. То есть, если хотя бы одна из частных производных 
или 
, то в точке 
нет экстремума.
Следовательно, экстремум следует искать в тех точках, в которых обе частные производные равны нулю. Так же как и для функции одной переменной, экстремум может быть и в точках, где функция не является дифференцируемой. Множество точек, в которых функция не является дифференцируемой, вместе с множеством стационарных точек образует множество критических точек.
15. Дайте определение максимума функции двух перемен-
ных.
Функция 
имеет в точке 
максимум, если существует такая проколотая окрестность точки 
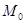, что для всех точек 
из этой окрестности (то есть достаточно близких к точке 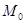и отличных от неё) выполняется неравенство
.
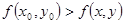16. Дайте определение минимума функции двух переменных
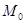Функция имеет в точке минимум, если существует такая проколотая окрестность точки , что для всех точек из этой окрестности выполняется неравенство
.
Максимум и минимум называют экстремумами функции.
Точка , в которой функция достигает своего максимума или минимума, называется точкой экстремума.
17. Сформулируйте необходимое условие существования экс-
тремума функции двух переменных.
Если функция 
дифференцируема в окрестности точки 
и имеет в этой точке экстремум (максимум или минимум), то 
(или 
).
18. Сформулируйте достаточное условие существования экс-
тремума функции двух переменных.
Пусть 
— стационарная точка функции , и в этой точке функция имеет непрерывные вторые частные производные. Положим 
, 
, 
, 
. Тогда
1. если 
, то функция имеет экстремум в точке 
, причём если 
(
), то это локальный максимум, а если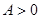 
(
), то локальный минимум;
2. если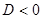 
, то в точке нет экстремума;
3. если 
, то экстремум может быть, а может и не быть; здесь требуется дополнительное исследование.
19. Дайте определение условного экстремума функции не-
скольких переменных.
Условным экстремумом функции 
называется максимум или минимум этой функции, достигаемый при условии, что n аргументов функции связаны между собой уравнениями 
, 
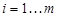, причем 
.
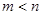20. Дайте определение многочлена Лагранжа.
Для нахождения условных экстремумов составляют функцию Лагранжа:
,
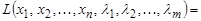
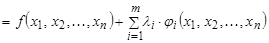где 
, - некоторые вспомогательные неизвестные.
Требуется, чтобы функции 
, 
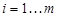, , были определены, непрерывны и непрерывно дифференцируемы.
После этого решают задачу нахождения экстремума функции Лагранжа – функции 
переменных 
. Условный экстремум функции 
будет достигаться при тех же значениях переменных.
Стационарные точки, то есть точки, в которых может быть условный экстремум, определяются из системы:
.
Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа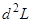 
в стационарной точке при условии, что 
.
Второй дифференциал находят по формуле
и вычисляют его значение в стационарной точке.
Если 
– стационарная точка, то функция 
имеет в точке 
условный максимум, если в этой точке 
, и условный минимум, если 
. Если знак 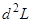переменный, то экстремума в этой точке нет. Если же 
или 
, то требуется дополнительное исследование.
21. Сформулируйте необходимое и достаточное условия су-
ществования условного экстремума.
22. Дайте определение производной функции по заданному
направлению.
23. Дайте определение градиента.
Градиентом скалярного поля 
называется вектор, координатами которого являются частные производные поля по переменным 
. Для градиента используют обозначение:
.
24. Сформулируйте геометрический смысл градиента.
1. Градиент показывает направление наибольшего возрастания поля в данной точке.
2. Модуль градиента равен наибольшей скорости возрастания поля в данной точке.
3. Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
4. Если имеется функция двух переменных 
, то вектор 
лежит в плоскости 
и направлен по нормали к линии уровня 
.
25. Дайте определение двойного интеграла.
26. Сформулируйте геометрический смысл двойного инте-
грала.
27. Дайте определение повторного интеграла.