Поиск кратчайших путей в сети.




Подобные задачи возникают при выборе маршрутов в вычислительных сетях и транспортных системах. В вычислительных сетях решение подобных задач определяет состав и структуру сетевых протоколов для обслуживания движения пакетов информации. По данным о загрузке каналов вычисляется наиболее оптимальный маршрут прохождения пакета информации. При нахождении такого пути к пакету добавляется заголовок, в котором содержится указывают перечень узлов для перехода от вершины хi к вершине хj или очередную вершину перехода. В транспортных системах решение подобных задач определяет наиболее экономный по стоимости или по времени маршрут движения транспортной единицы.

Каждая вершина в таком графе используется только один раз, а длина кратчайшего пути определится суммой весов ребер для перехода ni,j=(хi;...хk;...хj):

Li,j=m,nå lm,n, где i£m, n£j, m¹n.

Для поиска кратчайших путей есть несколько алгоритмов. Алгоритмы Форда-Беллмана и Дейкстра позволяют найти кратчайшие пути от заданной вершины графа до любой другой. В результате этих вычислений формируется

граф типа “дерево” с корнем в заданной вершине. Алгоритмы Флойда и Данцига позволяют искать кратчайшие пути между любой парой вершин графа типа сеть.

хp li,p lp,j
 
 


xj li,j xj

В основе всех алгоритмов лежит операция сравнения двух простых маршрутов. На рис. 30 показаны два простых маршрута, соединяющих вершины хi и хj. Выбор кратчайшего пути между вершинами хi и хj есть результат сравнения длин двух маршрутов, т.е. Li,j=min{li,j; (li,p+ lp,j)}. Если существует несколько вершин, смежных с вершинами хi и хj следует выполнять процедуру последовательно, сравнивая длины двух Рис. 30 Сравнение маршрутов. маршрутов для каждой вершины.

Алгоритм Флойда. Для того, чтобы выбирать кратчайшие путь и переходы между вершинами xi и xj, необходимо использовать две матрицы: матрицу кратчайших путей ║l(n;n)║ и матрицу кратчайших переходов ║n(n;n)║, которые позволяют вычислять и сравнивать различные маршруты через базовую вершину графа.

Вершина хp в матрице кратчайших путей называется базовой, а строка и столбец матрицы ║lp║ - базовыми (выделены в матрице заливкой), если она позволяет сравнивать кратчайшие пути между любой парой вершин xi и xj, смежных с вершиной хp. Базовая вершина позволяет найти путь из вершины xi в вершину xj через вершину xp по формуле lij=(lip+ lpj), представить этот результат для сравнения с имеющимся значением lij и выбрать кратчайший путь. Если в качестве базовой, использовать последовательно все вершины, начиная с вершины х0,

np x0 .. xi xp xj .. xn
x0 x0 .. xi xp xj .. xn
.. x0 .. xi xp xj .. xn
xi x0 .. xi xp xj .. xn
xp x0 .. xi xp xj .. xn
xj x0 .. xi xp xj .. xn
.. x0 .. xi xp xj .. xn
xn x0 .. xi xp xj .. xn
lp x0 .. xi xp xj .. xn
x0   .. l0i ∞ l0j .. l0n
.. ..   .. .. .. .. ..
xi li0 ..   lip lij .. lin
xp ∞ .. lpi   lpj .. lpn
xj lj0 .. lji ljp   .. ljn
.. .. .. .. .. ..   ..
xn ln0 .. lni lnp lnj .. 0nn

то за p=(n-1) шагов итерации можно найти кратчайшие пути между любой парой вершин. Для p=0 матрица ║l0║ есть матрица весов графа.

Матрица переходов np производна относительно матрицы кратчайших путей. Для p=0 элементы матрицы n0 есть концевые вершины перехода из хi в хj. Поэтому в каждом столбце хj матрицы n0 указана вершина хj. Результатом p-го шага итерации происходит замена вершины перехода вершиной кратчайшего перехода по формулам:

а) если (li,p+ lp,j)p³li,jp, то ni,j (p+1)= ni,j p=хj;

б) если (li,p+ lp,j)p<li,jp, то ni,j (p+1)=хp.

Следовательно, для анализа n-вершинного графа необходимо последовательно построить n матриц кратчайших путей и кратчайших переходов.

 

Итак, по алгоритму Флойда:

шаг 1: составить таблицы: матрицу весов ║lp║ и матрицу переходов ║np║ для p=0, где p – шаг итерации;

шаг 2: определить вершину p базовой и выделить базовые строки и столбец;

шаг 3: вычеркнуть строки и столбцы, базовые элементы которых имеют значение ¥, т.к. (li,p+¥) и (¥+ lp,j) всегда больше конечного значения li,j;

шаг 4: сравнить каждый невычеркнутый элемент lijp с суммой (li,p+ lp,j)p для формирования значений li,j и ni,j на очередном шаге итерации:

a) если (li,p+ lp,j)p<li,jp, то li,jp+1=(li,p+ lp,j)p, а ni,j (p+1)=p;

b) если (li,p+ lp,j)p>li,jp, то li,jp+1=li,jp; ni,j (p+1)= ni,j p.

шаг 5: если p<n, то принять p=p+1 и вернуться к шагу 4, иначе конец.

 
 

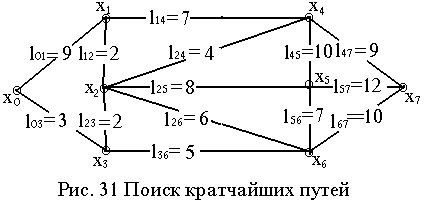Пример: Найти кратчайшие пути между вершинами графа (см. рис. 31).

 

Ниже таблицами показан процесс вычисления от p=0 до p=7

l0 x0 x1 x2 x3 x4 x5 x6 x7   n0 x0 x1 x2 x3 x4 x5 x6 x7
x0     ∞   ∞ ∞ ∞ ∞   x0 x0 x1 x2 x3 x4 x5 x6 x7
x1       ∞   ∞ ∞ ∞   x1 x0 x1 x2 x3 x4 x5 x6 x7
x2 ∞             ∞   x2 x0 x1 x2 x3 x4 x5 x6 x7
x3   ∞     ∞ ∞   ∞   x3 x0 x1 x2 x3 x4 x5 x6 x7
x4 ∞     ∞     ∞     x4 x0 x1 x2 x3 x4 x5 x6 x7
x5 ∞ ∞   ∞           x5 x0 x1 x2 x3 x4 x5 x6 x7
x6 ∞ ∞     ∞         x6 x0 x1 x2 x3 x4 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                       
l1 x0 x1 x2 x3 x4 x5 x6 x7   n1 x0 x1 x2 x3 x4 x5 x6 x7
x0     ∞   ∞ ∞ ∞ ∞   x0 x0 x1 x2 x3 x4 x5 x6 x7
x1           ∞ ∞ ∞   x1 x0 x1 x2 x0 x4 x5 x6 x7
x2 ∞             ∞   x2 x0 x1 x2 x3 x4 x5 x6 x7
x3         ∞ ∞   ∞   x3 x0 x0 x2 x3 x4 x5 x6 x7
x4 ∞     ∞     ∞     x4 x0 x1 x2 x3 x4 x5 x6 x7
x5 ∞ ∞   ∞           x5 x0 x1 x2 x3 x4 x5 x6 x7
x6 ∞ ∞     ∞         x6 x0 x1 x2 x3 x4 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l2 x0 x1 x2 x3 x4 x5 x6 x7   n2 x0 x1 x2 x3 x4 x5 x6 x7
x0           ∞ ∞ ∞   x0 x0 x1 x1 x3 x1 x5 x6 x7
x1           ∞ ∞ ∞   x1 x0 x1 x2 x0 x4 x5 x6 x7
x2               ∞   x2 x1 x1 x2 x3 x4 x5 x6 x7
x3           ∞   ∞   x3 x0 x0 x2 x3 x1 x5 x6 x7
x4             ∞     x4 x1 x1 x2 x1 x4 x5 x6 x7
x5 ∞ ∞   ∞           x5 x0 x1 x2 x3 x4 x5 x6 x7
x6 ∞ ∞     ∞         x6 x0 x1 x2 x3 x4 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
l3 x0 x1 x2 x3 x4 x5 x6 x7   n3 x0 x1 x2 x3 x4 x5 x6 x7
x0               ∞   x0 x0 x1 x1 x3 x2 x2 x2 x7
x1               ∞   x1 x0 x1 x2 x2 x2 x2 x2 x7
x2               ∞   x2 x1 x1 x2 x3 x4 x5 x6 x7
x3               ∞   x3 x0 x2 x2 x3 x2 x2 x6 x7
x4                   x4 x2 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x2 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x2 x2 x2 x3 x2 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l4 x0 x1 x2 x3 x4 x5 x6 x7   n4 x0 x1 x2 x3 x4 x5 x6 x7
x0               ∞   x0 x0 x3 x3 x3 x3 x3 x3 x7
x1               ∞   x1 x3 x1 x2 x2 x2 x2 x2 x7
x2               ∞   x2 x3 x1 x2 x3 x4 x5 x6 x7
x3               ∞   x3 x0 x2 x2 x3 x2 x2 x6 x7
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l5 x0 x1 x2 x3 x4 x5 x6 x7   n5 x0 x1 x2 x3 x4 x5 x6 x7
x0                   x0 x0 x3 x3 x3 x3 x3 x3 x4
x1                   x1 x3 x1 x2 x2 x2 x2 x2 x4
x2                   x2 x3 x1 x2 x3 x4 x5 x6 x4
x3                   x3 x0 x2 x2 x3 x2 x2 x6 x4
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7                   x7 x4 x4 x4 x4 x4 x5 x6 x7
                                     
l6 x0 x1 x2 x3 x4 x5 x6 x7   n6 x0 x1 x2 x3 x4 x5 x6 x7
x0                   x0 x0 x3 x3 x3 x3 x3 x3 x4
x1                   x1 x3 x1 x2 x2 x2 x2 x2 x4
x2                   x2 x3 x1 x2 x3 x4 x5 x6 x4
x3                   x3 x0 x2 x2 x3 x2 x2 x6 x4
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7                   x7 x4 x4 x4 x4 x4 x5 x6 x7
                                     
                                       
l7 x0 x1 x2 x3 x4 x5 x6 x7   n7 x0 x1 x2 x3 x4 x5 x6 x7
x0                   x0 x0 x3 x3 x3 x3 x3 x3 x4
x1                   x1 x3 x1 x2 x2 x2 x2 x2 x4
x2                   x2 x3 x1 x2 x3 x4 x5 x6 x4
x3                   x3 x0 x2 x2 x3 x2 x2 x6 x4
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7                   x7 x4 x4 x4 x4 x4 x5 x6 x7

 

По матрицам ||l7|| и ||ni,j 7|| можно найти длину кратчайшего перехода между любой парой вершин исходного графа. Например, между вершинами х0 и х7 длина кратчайшего пути равна 18, а переход n07=(х0;х3;х2;х4;х7), между вершинами х1 и х6 длина кратчайшего пути равна 8, а переход n16=(х1;х2;х6) и т.д.

При решении практических задач возникает необходимость поиска нескольких путей, частично - упорядоченных по возрастанию относительно кратчайшего. Такие задачи возникают при временной загруженности канала на определенном участке или неисправности узла. Для решения подобных задач разработаны обобщенные алгоритмы Флойда.

 

3.4.4 Поиск максимального потока и его распределения в сети

При обмене информацией между абонентами вычислительной сети, при параллельных вычислениях на многомашинном комплексе, когда решение задачи распределено между несколькими процессорами, при использовании в вычислительной сети общей памяти, когда каждый процессор получает доступ к общим модулям на ограниченный отрезок времени, возникает задача передачи максимального объема информации в заданный отрезок времени. При работе транспортной системы, когда осуществляется обмен транспортными единицами между узлами сети возникает задача передачи максимального числа транспортных единиц в заданный отрезок времени. При передаче энергии в электрических сетях, жидкости в трубопроводных системах возникает задача распределения и передачи максимального объема энергии или вещества в заданный отрезок времени.

Объем информации, энергии или вещества, передаваемый от узла xi к узлу xj, называют потоком и обозначают jij.

Граф, являющийся образом транспортной системы, называют сетью. Особенностью сети является отсутствие петель и кратных дуг, ориентация всех отрезков линий, т.е. наличие дуг в графе, наличие вершины-истока и вершины-стока в сети.

Наибольший поток, который может пропустить дуга (xi, xj), называют пропускной способностью дуги и обозначают сij.

Очевидно, что 0£jij£ сij.

В вершине-истоке х0 величина потока есть сумма потоков по всем дугам, исходящим из вершины х0, т.е. j=åij0i+.

В вершине-стоке хk величина потока есть сумма потоков по всем дугам, заходящим в вершину хk, т.е. j=åijik-.

Для любой промежуточной вершины хi сумма исходящих потоков равна сумме заходящих потоков, т.е. åjjij+=åkjik-.

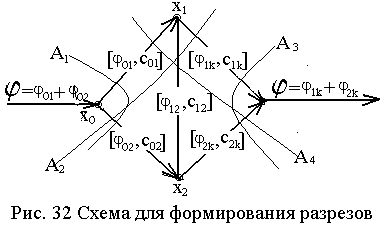
На рис. 32 показана условная сеть, содержащая вершину-исток х0, вершину-сток хk и две промежуточные вершины хi и хj. На каждой дуге в круглых скобках приведены обозначения потока и пропускной способности соответствующей дуги. При этом поток, подводимый к сети равен j=(j0i+j0j), поток отводимый от сети равен j=(jik+jjk), поток из вершины хi в вершину хj равен jij. Для вершины хi имеем j0i=(jij+jik), для вершину хj - jjk=(j0j+jij).

  Разрез пропускная способность дуги Сij пропускная способность
  С0i С0j Сij Сik Сjk разреза СAi
А1           С0i+ С0j
А2           С0j+Сij+Сik
А3           Сik+Сjk
А4           С0i+Сij+Сjk

Если множество вершин графа разбить на два непересекающихся подмножества, одно из которых содержит вершину-исток, а другое - вершину-сток, то множество дуг, соединяющих эти два множества, формируют разрез А, пропускная способность которого равна сумме пропускных способностей дуг. Таких разрезов может быть несколько.

Например, для А1 имеем Х’={x0} и X\Х’={хi, хj, хk}, для А2: Х’={х0, хi} и X\Х’={хj, хk}, для А3: Х’={х0, хi, xj} и X\Х’={хk}, для А4: Х’={х0, хj} и X\Х’={xi, хk}. Очевидно, что величина максимального потока ограничена минимальной пропускной способностью разреза, т.е. jmax=min{сAi}.

Итак, максимальный поток в сети с заданными пропускными способностями дуг графа можно находить, вычисляя пропускные способности всех дуг и выбирая среди них - минимальное. Однако при таком решении задачи остается неизвестным распределение потока по дугам графа.

Для поиска распределения потока по дугам графа разработано несколько алгоритмов, особое место среди которых занимает алгоритм Форда-Фалкерсона, суть которого состоит в разметке вершин графа. Метка вершины графа указывает на возможность изменения потока через данную вершину и указывает источник этого изменения. На рис. 33 дан фрагмент сети, объясняющий суть алгоритма.

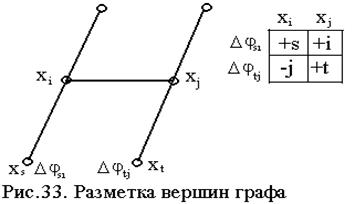
Если по дуге (хs, хi) возможно увеличение потока, т.е. j si< csi, то вершину хi следует пометить +s, что указывает на источник увеличения потока. Если по дуге (хi, хj) возможно увеличение потока j ij< cij, то вершину хj пометить +i. Это означает, что приращение потока Djsi пойдет по направлению дуги (хi, хj) от вершины хs.

Если по дуге (хt, хj) возможно увеличение потока, т.е. j tj< ctj, то вершину хj следует пометить +t, что указывает на источник увеличения потока. Однако, если вершина хj не имеет пометки +i, то для увеличения потока в фрагменте сети, следует уменьшить поток в дуге (хi, хj) и направить его далее по другим дугам фрагмента на сток. Для указания вершины, от которой необходимо уменьшить поток, ставят пометку –j. Это означает что на участке (хi, хj) поток должен быть уменьшен на величину Djtj.

Следует отметить, что вершины хi и хj могут иметь одновременно по нескольку подходящих и отходящих дуг. В примере, показанном на рис. 33 одновременно при допустимых Dj si и Dj tj могут быть для вершины хj две метки +t и +i для вершины хi также две метки +s и -j, что свидетельствует о свободе выбора приращения потока либо на величину Dj si, либо Dj tj.

Если дуга (хs, хi) насыщена, т.е. j si=csi, то метку +s у вершины хi ставить нельзя. Если насыщена дуга (хt, хj), т.е. j tj=ctj, то метку +t у вершины хj ставить нельзя.

Если вершина хj не помечена, то нельзя ставить метку -j у вершины хi. Когда обе вершины графа (хi и хj) не имеют меток, то это означает невозможность приращения потока. Так достигают максимального значения потока от вершин-истоков хs и хt по дугам к вершинам - стокам хi и хj.

Алгоритм Форда-Фалкерсона.

шаг 1: присвоить всем вершинам графа индексы 0,1,2,...k; где 0-индекс вершины-истока графа, k -индекс вершины-стока графа;

шаг 2: присвоить начальной вершине метку “0”;

шаг 3: все непомеченные вершины хi, в которые идут ненасыщенные дуги из помеченной вершины хs, пометить индексом “+s”, что свидетельствует о возможности увеличения потока из вершины хs по дуге (хs, хi);

шаг 4: все непомеченные вершины хi, из которых идут дуги (насыщенные или ненасыщенные) в помеченную вершину хj, пометить индексом “-j”, что свидетельствует о возможности уменьшения потока в вершину хj по дуге (хi, хj);

шаг 5: если в результате этих операций окажется помеченной вершина-сток xk, то между начальной и конечной вершинами сети найдется маршрут, все вершины которого различны и с точностью до знака помечены индексами предыдущих вершин, формирующих переход, по которому можно увеличить поток, и перейти к шагу 6, иначе конец.

шаг 6: увеличить поток в маршруте, сформированном на шаге 5, на единицу и перейти к шагу 3.

Пример: На рис. 34 дан граф. Каждой дуге графа (хi, хj) приписаны величина потока и пропускная способность (jij,cij).

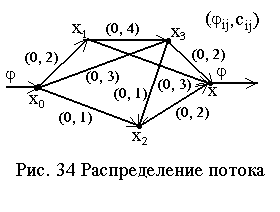Все расчеты по алгоритму сведены в две таблицы. В табл. а) на каждом шаге итерации для каждой вершины графа указаны возможные метки, а в табл. b) даны приращения потока по дугам (хi;хj). Символом “ “ в табл. b) показаны насыщенные дуги графа. В результате выполнения первого шага итерации возможны маршруты: n0k={(хk, х1, х0); (хk, х2, х0); (хk, х2, х3, х0); (хk, х2, х3, х1, х0); (хk, х3, х0); (хk, х3, х1, х0)}, из множества которых был выбран маршрут m = (хk, х3, х0).

табл. а)



Поделиться:




Поиск по сайту

©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2022-09-22 Нарушение авторских прав и Нарушение персональных данных
 

Поиск по сайту:

Читайте также:

Деталирование сборочного чертежа

Когда производственнику особенно важно наличие гибких производственных мощностей?

Собственные движения и пространственные скорости звезд

Тема 11. Банковские риски и способы их оценки

Опросник «Активность повседневной жизни»

Интересно:

Роль энергетики в жизни и развитии общества

Что такое грех в христианстве?

Роль музыки в эстетическом воспитании

Как защитить исследовательскую работу (проект)

Обратная связь