План лекции:
1. Определение комплексного числа.
2. Геометрическое изображение комплексных чисел.
3. Тригонометрическая форма записи комплексного числа.
4. Действия над комплексными числами.
5. Формула Эйлера. Показательная форма записи комплексных чисел.
Содержание лекции:
Вопрос 1. Определение комплексного числа.
Число 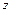 вида
вида 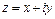 , где
, где 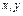 - любые действительные числа, а
- любые действительные числа, а 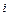 - так называемая мнимая единица, называется комплексным числом.
- так называемая мнимая единица, называется комплексным числом.
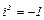 или
или 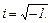
Действительные числа 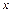 и
и 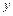 называются соответственно действительной и мнимой частями комплексного числа
называются соответственно действительной и мнимой частями комплексного числа 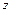 и обозначаются
и обозначаются 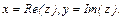
Рассмотрим частные случаи комплексных чисел.
· Пусть 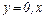 - любое действительное число. Тогда
- любое действительное число. Тогда 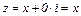 становится действительным числом.
становится действительным числом.
· Пусть 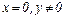 . Тогда
. Тогда 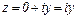 - чисто мнимое число.
- чисто мнимое число.
Таким образом, все действительные числа и все чисто мнимые числа входят в множество комплексных чисел.
Два комплексных числа 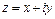 и
и 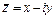 называются сопряженными комплексными числами.
называются сопряженными комплексными числами.
Сравнение комплексных чисел осуществляется по правилам:
1. Два комплексных числа 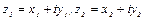 считаются равными, если
считаются равными, если 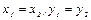 .
.
2. Комплексное число 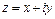 равно нулю только тогда, когда
равно нулю только тогда, когда 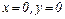 одновременно.
одновременно.
3. Операции <, > не имеют смысла на множестве комплексных чисел.
Вопрос 2. Геометрическое изображение комплексных чисел.
Рассмотрим декартову прямоугольную систему координат ХОУ на плоскости. Каждой точке плоскости при этом соответствуют вполне определенные координаты 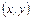 , а следовательно, и вполне определенное комплексное число
, а следовательно, и вполне определенное комплексное число 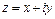 . Обратно, каждому к
. Обратно, каждому к 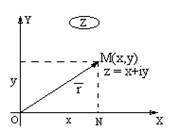 комплексному числу
комплексному числу 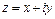 соответствует вполне определенная пара действительных чисел
соответствует вполне определенная пара действительных чисел 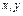 , а следовательно, и вполне определенная точка плоскости
, а следовательно, и вполне определенная точка плоскости 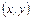 . Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа
. Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа 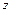 , называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа
, называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа 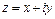 можно считать также и вектор
можно считать также и вектор 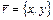 .
.
Вопрос 3. Тригонометрическая форма записи комплексного числа.
Длина вектора, изображающего комплексное число 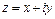 ,
, 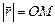 называется модулем комплексного числа.
называется модулем комплексного числа.
Угол, образуемый этим вектором с положительным направлением действительной оси (<MON), называется аргументом комплексного числа.
Обозначение: модуль 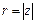 ,
,
аргумент 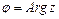 .
.
Из прямоугольного треугольника OMN

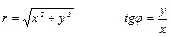 .
.
В качестве главного значения аргумента комплексного числа обычно выбирают значение 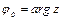 , определенное неравенствами
, определенное неравенствами
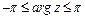 ,
,
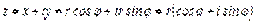 .
.
Итак, 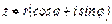 называется тригонометрической формой записи комплексного числа.
называется тригонометрической формой записи комплексного числа.
Пример. Записать в тригонометрической форме комплексные числа:
1. 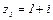
2. 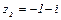
3. 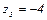
4. 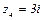 .
.
Решение:
1. 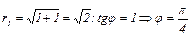
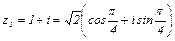 .
.
2. 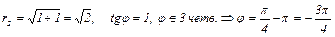 .
.
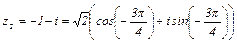 .
.
3. 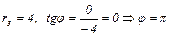
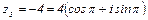 .
.
4. 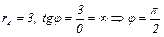
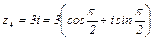 .
.
Вопрос 4. Действия над комплексными числами.
1. Сложение.
Суммой двух комплексных чисел 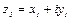 и
и 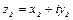 называется комплексное число
называется комплексное число 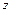 , определяемое равенством
, определяемое равенством
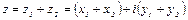 .
.
Из определения вытекают следующие законы сложения:
- Переместительный: 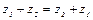
- Сочетательный: 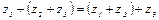
2. Вычитание.
Вычитание комплексных чисел определяется как действие, обратное сложению. Вычесть из числа 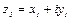 число
число 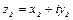 значит найти такое число
значит найти такое число 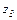 , чтобы имело место равенство:
, чтобы имело место равенство: 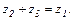 Число
Число 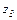 называется разностью чисел
называется разностью чисел 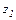 и
и 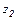 и обозначается
и обозначается 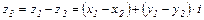 .
.
Вычитание всегда выполнимо.
3. Умножение.
Произведением 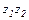 двух комплексных чисел
двух комплексных чисел 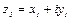 и
и 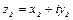 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством 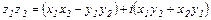 .
.
Из определения следуют законы:
· Переместительный 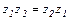
· Сочетательный 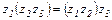
· Распределительный 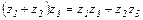 .
.
4. Деление.
Деление – действие, обратное умножению. Разделить комплексное число 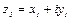 на комплексное число
на комплексное число 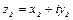 значит найти такое число
значит найти такое число 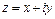 , чтобы имело место равенство
, чтобы имело место равенство 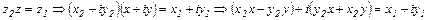 .
.
Тогда получаем систему для определения 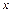 и
и 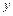 :
:
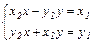
Система всегда разрешима, т.к. определитель
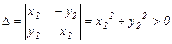 .
.
Число 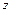 называется частным.
называется частным.
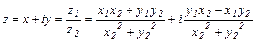 .
.
Итак, чтобы разделить одно комплексное число на другое, надо числитель и знаменатель дроби умножить на комплексное число, сопряженное числу, стоящему в знаменателе.
Пример.
Выполнить все действия над комплексными числами 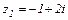 и
и 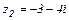 .
.
Решение
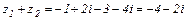
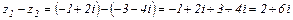
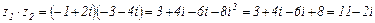
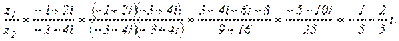
Умножение и деление комплексных чисел, заданных в тригонометрической форме.
Пусть 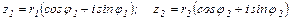 .
.
Тогда 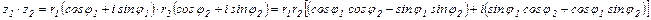
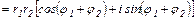 .
.
Следовательно, при умножении комплексных чисел их модули умножаются, а аргументы складываются: 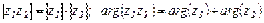 .
.
Деление комплексных чисел, записанных в тригонометрической форме, приводит к формуле:
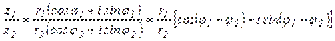 .
.
Справедливость этого равенства легко проверить обратным действием (умножением). Т.о., модуль частного двух комплексных чисел равен частному модулей делимого и делителя; аргумент частного равен разности аргументов делимого и делителя.
Пример
Выполнить все действия умножения и деления комплексных чисел 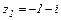 и
и 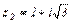 , представив их в тригонометрической форме.
, представив их в тригонометрической форме.
5. Возведение в степень. Формула Муавра.
Из правила умножения комплексных чисел в тригонометрической форме следует правило возведения в целую положительную степень n комплексного числа.
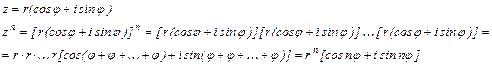
Итак 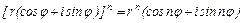
Эта формула называется формулой Муавра. Она показывае, что при возведении комплексного числа в целую положительную степень модуль возводится в эту степень, а аргумент умножается на показатель степени.
Пример
Вычислить 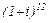
6. Извлечение корня.
Корнем n степени из комплексного числа 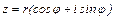 называтся также комплексное число
называтся также комплексное число 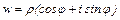 , n – я степень которого равняется подкоренному числу, т.е.
, n – я степень которого равняется подкоренному числу, т.е. 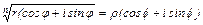 .
.
Если 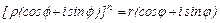 или
или 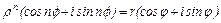
так 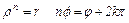
откуда 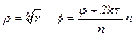
где k - любое число, 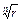 - арифметическое значение корня.
- арифметическое значение корня.
Следовательно 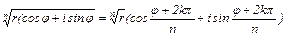
Пример
Найти все значения 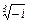
Решение
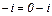 приведём к тригонометрической форме:
приведём к тригонометрической форме: 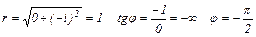
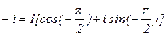
Следовательно 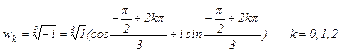
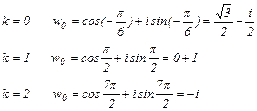
Если придавать значения 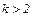 , то корни будут повторяться.
, то корни будут повторяться.
Действительно, при 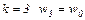
Пример.
Решить двучленное уравнение 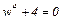
Решение.
Нахождение корней уравнения сводится к задаче: найти все значения корня 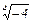
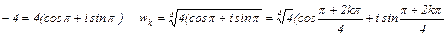
Вопрос 5. Формулы Эйлера. Показательная форма комплексного числа.
Из математического анализа известно разложение функций 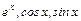 в степенной ряд:
в степенной ряд:
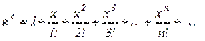 (1)
(1)
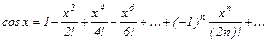 (2)
(2)
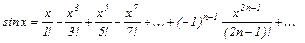 (3)
(3)
Условимся считать, что формула (1) имеет место и при 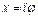 , тогда получим:
, тогда получим:
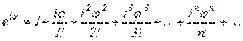
Учитывая, что
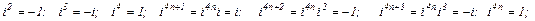
и отделяя здесь действительные и чисто мнимые члены, получим:
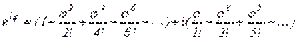

На основании формул (2) и (3) заключаем, что сумма рядов, стоящих в скобках, соответственно равна cosj и sinj.
Поэтому получаем: 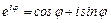 (4)
(4)
Это есть формула Эйлера.
Заменяя в формуле (4) j на -j и учитывая при этом что cosj - чётная, sinj - нечётная функции, получим:
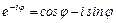 (5)
(5)
Разрешив равенства (4) и (5) относительно cosj и sinj получим ещё 2 формулы Эйлера:
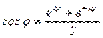 (6)
(6)
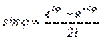 (7)
(7)
Формула (4) даёт новую показательную форму комплексного числа, имеющего модуль r и аргумент j:
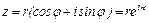
Пример
Написать в показательной форме комплексные числа:
а) 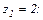 б)
б) 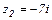 ; в)
; в) 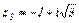 ; г)
; г) 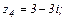 д)
д) 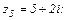
Решение
а) 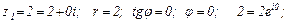
б) 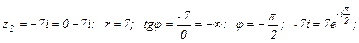
в) 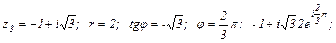
г)