Растяжение, сжатие. Расчет бруса

Для заданного бруса, нагруженного продольными силами построить эпюры продольных сил и нормальных напряжений, проверить его прочность, и определить перемещение свободного конца бруса, приняв при этом допускаемое напряжение [σ]=160 Мп, коэффициент пропорциональности Е = 2*10 Мп

Решение

1. Разбиваем брус на участки.

2. Используя метод сечений, определяем продольные силы по участкам, строим эпюру продольных сил.

N=±ΣF_ix

N_I=

N_II=

N_III=

Рисунок - Схема конструкций бруса

с эпюрами N и напряжени й.

2. Определяем нормальное напряжение по длине бруса и строим эпюру напряжений σ=N/A

σ₁=N_I/A₁=

σ₂=N_II/A₂=

σ₃=N_III/A₂=

Опасным являетсяучасток, где | σ_мах| =

4. Производим проверку прочности бруса в опасном сечении σ_мах≤[σ]

Процент недогрузки (перегрузки):

δ=|(σ – [σ]) |*100% /[σ] =

Для уменьшения процента недогрузки необходимо изменить площадь поперечного сечения. Пересчитаем площадь в опасном сечении при заданных нагрузках. Примем условно, что σ в опасном сечении получилось 160 МПа

A = N/|σ| =

5. Определяем перемещение свободного конца бруса.

Δl_полн. = ΣΔli;

Δl_полн. = Σσ₁·l₁/E =

– брус укорачивается (удлиняется)

 

 

Рисунок 13- Заданная схема конструкции балки Рисунок 14- Балка, освобождённая от связей

Решение:

1. Рассмотрим равновесие балки АВ.

2. Освободим балку АВ от связей, действие связи заменим реакциями. Равномерно-распределенную нагрузку интенсивностью q заменим сосредоточенной силой Q, приложенной в центре участка действия нагрузки.

3. Используя условия равновесия для произвольной системы сил, определим реакцию стержня ВС

ΣМ_А(F)=0

4. Под действием силы R_BD= стержень работает на растяжение и продольная сила равна

|N_BD| = |R_BD| =

5. Определяем допустимое напряжение при растяжении:

σ = σ_пр / [n] = σ_max /[n]; σ=

6. Используя условия прочности при растяжении, определим требуемую площадь поперечного сечения стержня BD.

σ = N_BD / A ≤ [σ]; A ≥ N_BD/[σ]; A ≥

7. Определим требуемый диаметр стержня BD.

A = π·d²/4; ; d≥ Принимаем d=

8. По таблицам сортамента прокатной стали определим номер равнополочного уголка по требуемой площади A ≥ Атабл= №

2.3. Срез, смятие. Расчет шарнирного узла А . Рычаг, прикрепленный к опоре А удерживается в равновесии стержнем BD, Соединение в точках А, В и D шарнирное. Рычаг нагружен силой F=3 kH. Определить диаметр оси шарнира узла А из условия прочности на срез и проверить соединение на смятие, если a = 45 мм, b = 225 мм, α = 20°, [σсм] = 140 МПа, [τср] = 80 МПа.

 

Рисунок - Заданная схема конструкции рычага Рисунок -Конструкция узла А

Решение:

1. Рассмотрим равновесие рычага.

2. Освободим рычаг от связей, действие связей заменим реакциями.

3. Составим уравнения равновесия для полученной произвольной плоской системы сил, и определим реакцию опоры А.

Рисунок - рычаг освобожденный от связей

ΣF_IX = 0

ΣF_IY = 0

ΣM_A(F) = 0

Имеем систему 3-х уравнений с тремя неизвестными, то есть задача статически определяема.

R_AX= R_AY= R_A=

4. Поперечная сила для оси шарнира численно равна реакции опоры А. |Q|=|R_A|=

5. Используя условие прочности на срез, определим диаметр оси шарнира

τ_ср = Q/n* Aср ≤ [τ_ср] Аср= πd²/4 n=2

6. Определяем фактическое напряжение смятия и сравниваем его с допускаемым.

σ_см = R_A/A_CM ≤ [σ_см] Acм=d* =15 мм (По чертежу)

σ_см = R_A/d∙ =

Получается, что рабочее напряжение σ_{см =} ≤ [σ_см] = 140 мПа меньше, значит, условие прочности соблюдается. Соединение работает с недогрузкой (перегрузкой).

2.4. Кручение, расчет вала. Для стального трансмиссионного вала определить внешние вращающие моменты на ведущем и ведомом шкивах. Построить эпюру крутящих моментов для двух вариантов расположения шкивов. Первый вариант расположения шкивов принять согласно схеме задания. Второй вариант выбрать самостоятельно. Для рациональной схемы расположения шкивов, из условия прочности и жесткости определить диаметр вала, если выполнить его сплошным, и найти размеры кольца, если вал сделать полым. Диаметр вала считать по всей длине постоянным. Окончательное принимаемое значение диаметра вала округлить до ближайшего четного или оканчивающегося на 5 числа мм. Для вала кольцевого поперечного сечения принять отношение диаметров dвн/dнар = 0,65. Сравнить массу сплошного и полого вала, если известно: P2= кВт, P3= кВт, P4= кВт, n = об/мин, [τкр] = Н/мм2, [φотн] = град/м, G =8·104МПа

Рисунок - Заданная схема конструкции вала

Решение

1. Определить угловую скорость вала:

ω = π·n/30 = 3.14· = рад/с;

2. Мощность, передаваемая первым валом:

P₁ = P₂ + P₃ + P₄ = = кВ

3. Определим внешние вращающие моменты:

T = P/ω;

T₁ = P₁/ω₁ =

T₂ = P₂/ω₂ =

T₃ = P₃/ω₃ =

T₄ = P₄/ω₄ =

Проверка ΣT_ix = 0; T₁ + T₂ + T₃ + T₄ = 0;

0=0 => вращающие моменты найдены верно

4. Определяем крутящие моменты по участкам и строим эпюру моментов:

M_кр = ΣM_x(F);

M_кр1 = 0;

M_кр2 =

M_кр3 =

M_кр4 =

M_кр5 =

M_кр.мах =

 

Рисунок - Заданная схема конструкции Рисунок - Заданная схема конструкции

с эпюрой крутящих моментов с эпюрой крутящих моментов

(1 вариант расположение шкивов) (2 вариант расположение шкивов)

5. Поменяем местами 1 и 2 шкивы, построим эпюру крутящих моментов:

M_кр1 = 0;

M_кр2 =

M_кр3 =

M_кр4 =

M_кр5 =

M_кр.мах =

Рациональной является схема расположения шкивов, так как max момент равный, имеет большее значение.

6. Определяем диаметр вала для рациональной схемы расположения шкивов при M_кр.мах =

Сечение вала – круг:

Из условия прочности:

τ = V_кр/W_p ≤ [τ_кр]

W_p ≥ Mкр/[τ_кр] Wp=π·d³/16

Условие жесткости:

Φ₀ = 180·M_кр / π·G·I_p ≤ [φ_отн]

I_p ≥ 180· M_кр / π·G [φ_отн] I_p = π·d⁴/32

G=8*10⁴мПа (по условию) Принимаем окончательно d=

Сечение вала – кольцо:

Из условия прочности:

W_p ≥ Mкр/[τ_кр] с=dвн/dнар=0.65 (по условию)

Из условие жесткости:

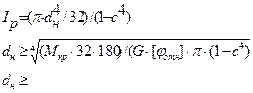
Принимаем окончательно dнар= dвн=0.65*dнар=

7. Определяем отношение масс валов с сечением круг и кольцо. Поскольку масса балки пропорциональна, площади ее поперечного сечения, то отношение масс валов одинаковой длины равно отношению площадей их сечений.

Площадь круглого сечения: A_кр = π∙d²/4 =

Площадь кольцевого сечения: A_к = π∙(dн²- dвн²)/4=

Отношение масс: A_кр/A_к =

Следовательно, вал кругового сечения в раз тяжелей кольцевого сечения.

 

2.5. Изгиб. Построение эпюр поперечных сил и изгибающих моментов. Для балки с заданными сосредоточенными нагрузками построить по характерным точкам эпюры поперечных сил и изгибающих моментов.

Решение:

1. Разделяем балку на участки по характерным точкам.

2. Определяем поперечные силы в характерных точках и строим эпюру поперечных

Q = ±∑F_IY

. Q =

Q =

Q =

Q =

Рисунок -Схема нагружения балки с Q =

эпюрами Q и Миз

3. Определяем изгибающие моменты в характерных точках и строим эпюры моментов Миз=±∑Мс(F)

M =

M =

M =

M =

M =

Решение

1. Рассмотрим равновесие балки

2. Освободим балку от связей, действие связей реакциями.

3. Найдем реакции опор, используя уравнения равновесия для произвольной плоской системы сил

Рисунок 21- Заданная схема конструкции балки

с эпюрой изгибающих моментов

ΣM_A(F) = 0 |

ΣM_B(F) = 0 |

R_B =

R_AY =

Поверка:

ΣF_IY = 0 |

0 = 0, значит вычисления выполнены верно.

4. Построим эпюру изгибающих моментов.

М_ИЗГ = ΣМ_С(F)

M =

M =

M =

M =

M =

Опасным является сечение в точке где возникает максимальный изгибающий момент.

5. Вычисляем осевой момент сопротивлений.

σ_ИЗГ = М_ИЗГ/W_Z ≤ [σ]; W_Z ≥ М_ИЗГ/[σ]

W_Z ≥ ≥

6. Подбираем сечение балки в виде:

А) двутавра

№ W_Z = A =

Б) сдвоенного швеллера

W_Z = W_Z(2шт)/2 = =

№ W_Z = A =

В) круга

W_Z = πd²/32

A = πd²/4

A =

Г)прямоугольника

h/b = 2 (по условию)

W_Z = 2/3∙b³

Вывод. Наиболее экономичными является такие формы поперечных сечений, которые имеют наименьшую площадь. Так как затраты материала при одинаковой длине балок пропорциональны площадям их поперечных сечений, то наиболее экономичным является сечение двутавр.