Путем от вершины A до вершины B в графе называется последовательность ребер, ведущая от A к B, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза. Путь называется простым, если он не проходит ни через одну из вершин графа более одного раза.
Циклом называется путь, в котором совпадают его начальная и конечная вершины.
Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза.
Путь (цикл) имеет длину n, если он содержит n ребер.
задача 1. Если у графа все простые циклы четной длины, то граф не имеет ни одного цикла нечетной длины.
задача 2. В стране Семерка 15 городов, каждый из которых соединен дорогами не менее, чем с 7 другими. Докажите, что из любого города можно добраться до любого другого (возможно с пересадками).
Две вершины A и B графа называются связными (несвязными), если в графе существует (не существует) путь с концами A и B.
Граф называется связным, если каждые его две вершины связные и несвязным в противном случае.
задача 3. Связный граф представляет собой простой цикл Û каждая его вершина имеет степень 2.
задача 4. Докажите, что граф с n вершинами, степень каждой из которых не менее (n-1)/2 является связным.
задача 5. В Тридевятом царстве лишь один вид транспорта - ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний - одна, а из всех остальных городов - по 20. Докажите, что из столицы можно долететь в Дальний (возможно, с пересадками).
задача 6. В стране из каждого города выходит 100 дорог и от любого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь от любого города можно добраться до любого другого.
|
|
При удалении ребра (AB) из графа получается граф с теми же вершинами и ребрами, кроме ребра (AB).
задача 7. Можно ли из полного графа с 17 вершинами удалить некоторые ребра так, чтобы степень каждой вершины равнялась 5?
Ребро с концами A и B называется мостом, если в графе после удаления этого ребра вершины A и B оказываются несвязными.
задача 8. Докажите, что следующие утверждения равносильны:
1) Ребро (AB) - мост;
2) (AB) - единственный путь, соединяющий вершины A и B;
3) Существуют вершины C и D (не обязательно отличные от A и B) такие, что каждый путь, соединяющий их, содержит A и B;
4) (AB) не принадлежит ни одному циклу.
задача 9. В графе все вершины имеют степень 3. Докажите, что в нем есть цикл.
Деревом называется связный граф не имеющий циклов.
задача 10. Докажите равносильность утверждений:
1). Граф G является деревом;
2). В графе G любые две вершины соединены простым путем;
3). Граф G связен, но при удалении любого ребра становится несвязным;
4). Граф G связен и число вершин в нем на 1 больше числа ребер.
Вершина графа, имеющая степень 1, называется висячей.
задача 11. Докажите, что в дереве всегда есть одна (две) висячие вершины.
задача 12. Докажите, что если для любой пары вершин графа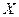 
и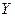 
выполнено неравенство 
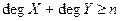, то в графе нет висячих вершин.
задача 13. Волейбольная сетка имеет вид прямоугольника размером 50´600 клеток. Какое наибольшее число веревочек можно перерезать так, чтобы сетка не распалась на куски?
задача 14. В некоторой стране 30 городов, причем каждый соединен с каждым дорогой. Какое наибольшее число дорог можно закрыть на ремонт так, чтобы из каждого города можно было проехать в каждый?
|
|
задача 15. Докажите, что в любом связном графе можно удалить вершину со всеми выходящими из нее ребрами так, чтобы он остался связным.
задача 16. В марсианском метро 100 станций, причем из любой станции можно доехать до любой другой. Забастовочный комитет хочет закрыть n из них, где 0<n<100. Забастовка считается гуманной, если между всеми незакрытыми станциями остается проезд. Докажите, что при любом n возможна гуманная забастовка.
задача 17. В стране 100 городов, некоторые из которых соединены авиалиниями. Известно, что от любого города можно долететь до любого другого (возможно, с пересадками). Докажите, что можно побывать в каждом городе, совершив не более а) 198 перелетов; б) 196 перелетов.
задача 18. Расстоянием между двумя произвольными вершинами дерева будем называть длину простого пути, соединяющего их. Удаленностью вершины дерева назовем сумму расстояний от нее до всех остальных вершин. Докажите, что в дереве, у которого есть две вершины с удаленностями, отличающимися на 1, - нечетное число вершин.
задача 19. Квадрат 8´8 выложили из спичек. Какое наименьшее число спичек надо убрать, чтобы с любого поля можно было пройти на любое другое, не перепрыгивая через спички?
Лесом называется несвязный граф, представляющий объединение деревьев.
задача 20. Докажите, что лес с k деревьями, содержащий n вершин имеет n-k ребер.