Домашние задания по дисциплине «Физика и естествознание»
Для студентов II курса IV семестра факультета ИБМ
Варианты домашних заданий
| Вариант | Номера задач | |||
| Модуль 5 ДЗ № 1 | Модуль 6 ДЗ № 2 | |||
| 1.1 | 2.1 | 3.1 | 4.1 | |
| 1.2.1 | 2.2 | 3.2.1 | 4.2 | |
| 1.2.2 | 2.3 | 3.2.2 | 4.3 | |
| 1.2.3 | 2.4 | 3.2.3 | 4.4 | |
| 1.3 | 2.5 | 3.2.4 | 4.5 | |
| 1.4 | 2.6 | 3.3.1 | 4.6 | |
| 1.5 | 2.7 | 3.3.2 | 4.7 | |
| 1.6 | 2.8 | 3.3.3 | 4.8 | |
| 1.7 | 2.9 | 3.3.4 | 4.9 | |
| 1.8 | 2.10 | 3.4.1 | 4.10 | |
| 1.9.1 | 2.11 | 3.4.2 | 4.11 | |
| 1.9.2 | 2.12.1 | 3.4.3 | 4.12 | |
| 1.9.3 | 2.12.2 | 3.4.4 | 4.13 | |
| 1.9.4 | 2.12.3 | 3.5.1. | 4.14 | |
| 1.10 | 2.12.4 | 3.5.2 | 4.15 | |
| 1.11 | 2.13.1 | 3.5.3 | 4.16 | |
| 1.12.1 | 2.13.2 | 3.5.4 | 4.17 | |
| 1.12.2 | 2.13.3 | 3.6 | 4.18 | |
| 1.12.3 | 2.13.4 | 3.7 | 4.19 | |
| 1.13 | 2.13.5 | 3.8 | 4.20 |
При выполнении домашних заданий рекомендуется использовать методические указания к решению задач по курсу общей физики. Авторы: Л.К. Мартинсон, Е.В. Смирнов. Разделы: «Квантовая природа излучения. Гипотеза Планка», «Волновые свойства частиц. Гипотеза де Бройля», «Уравнение Шредингера. Стационарные задачи квантовой механики», «Квантовая статистика Ферми – Дирака. Электронный газ», «Физика атомного ядра и элементарных частиц». Эти пособия можно найти на сайте кафедры физики МГТУ имени Баумана. Также рекомендуется использовать задачники: И.Е. Иродов «Задачи по общей физике», А.Г. Чертов, А.А. Воробьев «Задачник по физике», И.Е. Иродов «Атомная и ядерная физика».
Модуль 5. Домашнее задание № 1
Задача 1. Тепловое излучение. Фотоэффект
1.1. При увеличении температуры абсолютно черного тела в η = 2 раза длина волны, на которую приходится максимум испускательной способности этого тела, сокращается на Δλ = 0,8 мкм. Определите начальную температуру тела.
1.2. Определить, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды Т 0 = 295 К поддерживать его температуру равной Т (см. табл. 1). Потери считать обусловленными только излучением. Поглощательная способность меди аТ.
1.3. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость Rэ снизилась в n раз.
1.4. Температура внутренней поверхности муфельной печи при открытом отверстии (окне) площадью 30 см2 равна 1,3 кК. Принимая отверстие за черное тело, определить, какая часть мощности рассеивается стенками печи, если последняя потребляет 1,5 кВт.
1.5. Вследствие изменения температуры абсолютно черного тела максимум испускательной способности сместился с λ1 = 2,4 мкм до λ2 = 0,8 мкм. Как и во сколько раз изменилась энергетическая светимость Rэ этого тела?
1.6. Мощность (Р) излучения шара радиусом R = 10 см при некоторой постоянной температуре (Т) равна 1 кВт. Определить эту температуру, рассматривая шар как серое тело с поглощательной способностью аТ = 0,25.
1.7*. Полость объемом V = 1,0 л заполнена тепловым излучением при температуре Т = 1000 К. Определить теплоемкость CV этого излучения.
1.8. При поочередном освещении поверхности некоторого металла светом с длинами волн λ1 = 0,35 мкм и λ2 = 0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в η = 2 раза. Определить работу выхода с поверхности этого металла.
1.9. Определить красную границу фотоэффекта для указанного металла и максимальную скорость фотоэлектронов, вырываемых с его поверхности излучением с длиной волны λ = 250 нм (см. табл. 2)
1.10. Какая доля энергии фотона израсходована на работу вырывания фотоэлектронов, если красная граница фотоэффекта составляет λ0 = 307 нм и максимальная кинетическая энергия фотоэлектрона равна 1 эВ?
1.11. Максимальная скорость фотоэлектронов при освещении цезиевого электрода монохроматическим светом оказалась равной υ max = 0,55 Мм/с. Работа выхода для цезия Ав = 1,89 эВ. Определить длину волны света, падающего на электрод.
1.12. Определить энергию падающих фотонов и максимальную скорость фотоэлектронов, вырываемых с поверхности указанного металла, если фототок прекращается при приложении задерживающего напряжения U 0 (см. табл. 3).
1.13. Плоский серебряный электрод освещается монохроматическим излучением с длиной волны λ = 80 нм. Определите, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряженностью Е = 10 В/см. Красная граница фотоэффекта для серебра λ0 = 264 нм.
Таблица 1.
Таблица 2.
Таблица 3.
| Зад. | d, см | Т, К | аТ | Зад. | Металл | А, эВ | Зад. | Металл | А, эВ | U 0, B | ||
| 1.2.1 | 1,5 | 0,6 | 1.9.1 | Цинк | 3,74 | 1.12.1 | Барий | 2,29 | 7,1 | |||
| 1.2.2 | 2,0 | 0,5 | 1.9.2 | Железо | 4,36 | 1.12.2 | Титан | 3,92 | 6,4 | |||
| 1.2.3 | 2,5 | 0,4 | 1.9.3 | Медь | 4,47 | 1.12.3 | Золото | 4,58 | 5,0 | |||
| 1.9.4 | Никель | 4,84 |
Задача 2. Основы квантовой механики
2.1. Электрон с кинетической энергией ЕК = 4 эВ локализован в области размером l = 1 мкм. Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.
2.2. Поток нейтронов проходит через узкие радиальные щели в двух дисках из кадмия, поглощающего нейтроны. Диски насажены на общую ось так, что щели повернуты друг относительно друга на угол a. Диски вращаются с угловой скоростью w = 300 рад/c, расстояние между ними L = 1 м. Найти угол a, если длина волны де Бройля пропускаемых таким устройством нейтронов равна l = 0,1 нм.
2.3. Вычислить длину волны де Бройля теплового нейтрона, т.е. нейтрона, находящегося в тепловом равновесии с окружающей средой, имеющей комнатную температуру Т = 295 К.
2.4. Найти дебройлевскую длину волны молекул водорода, соответствующую их средней квадратичной скорости при температуре Т = 293 К.
2.5. Определить, какую ускоряющую разность потенциалов U должен пройти электрон, чтобы длина волны де Бройля для него была равна λ.
2.6. Электрон движется по окружности радиуса r = 0,5 см в однородном магнитном поле с индукцией В = 10 мТл. Определить длину волны де Бройля этого электрона.
2.7. Параллельный пучок электронов, движущихся со скоростью υ = 1 Мм/с, падает нормально на диафрагму с длинной щелью шириной b = 1 мкм. Пройдя щель, электроны рассеиваются и образуют дифракционную картину на экране, удаленном от плоскости щели на расстоянии l = 0,5 м. Определить ширину х центрального максимума интенсивности.
2.8. Определить длину волны де Бройля для электрона, находящегося в атоме водорода на боровской орбите с номером n.
2.9. Используя соотношение неопределенностей, оценить низший энергетический уровень электрона в атоме водорода. Принять линейные размеры атома l ~ 0,1 нм.
2.10. Приняв, что минимальная энергия нуклона в составе ядра атома равна Е = 10 МэВ, оценить, исходя из соотношения неопределенностей, линейные размеры ядра.
2.11. Оценить относительную ширину Δω/ω спектральной линии, если известны время жизни атома в возбужденном состоянии τ ≈ 10-8 с и длина волны излучаемого фотона λ = 0,55 мкм.
2.12. Микрочастица массой m находится в бесконечно глубокой прямоугольной потенциальной яме шириной l (0 < x < l) в указанном состоянии n. Определить энергию частицы Еп на соответствующем энергетическом уровне и вероятность W ее нахождения в указанном участке ямы x 1 < x < x 2 (см. табл. 4). Решение пояснить графически.
2.13. Электрон проходит через высокий прямоугольный потенциальный барьер шириной d = 0,5 нм. Высота U барьера больше энергии Е электрона на 2 %. Вычислить коэффициент прозрачности D, если энергия электрона принимает указанные значения (см. табл. 5).
Таблица 4.
Таблица 5.
|
| Зад. | n | x 1< x < x 2 | Зад. | Е, эВ | |
| 2.12.1 | 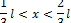
| 2.13.1 | |||
| 2.12.2 | 
| 2.13.2 | |||
| 2.12.3 | 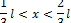
| 2.13.3 | |||
| 2.12.4 | 
| 2.13.4 |
Модуль 6. Домашнее задание № 2