Контрольная работа № 1
Вариант 1
1.  Построить график функции, заданной в полярных координатах:
Построить график функции, заданной в полярных координатах: 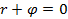 .
.
2. Зная график функции  (см. рис.),
(см. рис.),
построить графики функций  ;
;
 ;
;  ;
;  ;
;
 .
.
3. Даны последовательности nsin обосновать, какие из них являются неограниченными.
4. для последовательности { х ливость утверждений:
Привести таблицу истинности.
5. Сформулировать с помощью кванторов следующие утверждения:
а) lim f(x) = +00, б) Лх) -» b+O при х —» —оо и составить один график, на котором эти утверждения будут отражены.
6. Найти пределы:  2114 ПЗ — 14
2114 ПЗ — 14
cos 3х — cos 2х
3) lim 2

х а х —1
4) lim 
tg2x 5) lim 
tg—tga
 6) lim
6) lim
х
 8) lim
8) lim
Вариант 2
1. Построить график заданной неявно функции min(x,y) =.
| х | ||
2. Зная график функции у = f(x) (см. рис. 1), построить графии функций
а) у = f(—x); б) у = '• в) у = sgnf(x); f(x)

3. Даны последовательностей 2n + п(—, выяснить
и обосновать, какие из них являются ограниченными.
4. Для последовательности  выяснить и обосновать справедливость утверждений:
выяснить и обосновать справедливость утверждений:
1) УЕ>О 3no eN•. Уп>по lxnl>E.
2) УЕ>О eN: Ап? по 
3) УЕ>О ЗА eN: Зп>по lxnl<E.

Привести таблицу истинности.
5. Сформулировать с помощью кванторов следующие утверждения:
а) lim f(x) = Ь, б) f(x) b+O при х +00 и нарисовать
один график, в котором эти утверждения будут отражены. (3)
6. Найти пределы:
1) lim ctgx.


Вариант З
1. Построить график заданной параметричесюа функции

2. Зная графикфункции у = f(x) (см. рис. на стр. 554), постро-
ить графики фунющй а) у = —f(x); б) у = —; в) у = sgnf(x); f(x)

3. Даны последовательности п + п(—. Выяснить и п обосновать, какие из них яшшются бесконечно малыми.
4. рдля последовательности cos—n выяснить справедливость утверждений:
1) VE>O EN: Vn>no 
2) VE>0 3no eN: Зп2по lxnl>E. 3) УЕ>0 3no eN: ЗП>ПО 
4) ЗЕ>О Упо?N: Уп? по lxnl<E.
Сотавить таблицу истинности.
5. Сформулировать с помощью кванторов следующие утверждения:
а) limf(x) = оо; б) f(x) Ь при х —0 и нарисовать один
график, в котором эти утверждения будут отражены.
6. Найти пределы:

х
3) lim 
4) lim xsin—;  х arctg2x
х arctg2x
5)  lim
lim
 arcsin 3х
arcsin 3х
1-2х 2х
6) lim
 3-2х 7) lim еХ+1.
3-2х 7) lim еХ+1.
8) lim (хз +3х

Вариант 4
1. Построить график функции r = т, где 0 < < 2т.
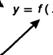 х х
| |
2. Зная график фундии у = f(x) (рис.), построить графики функций а) у = f(x + 1) + 2;
 в) у = sgnf(x);
в) у = sgnf(x); 
3. Привести пример ограниченной расходящейся последовательности. Построить график.
4. Для последовательности п + выяснить справедливость утверждений:
 eN: Уп>по
eN: Уп>по 
Составить таблицу истинности.
5. Сформулировать с помощью кванторов следующие утверпения:
 +00; б) Лх) при
+00; б) Лх) при  и нарисо-
и нарисо-
вать один график, в котором эти утверждения будут отражены.
6. Найти пределы:
4) 


sin х

Контрольная работа № 2
Вариант 1 
1. Исследовать на непрерывность в точке х = 0 функцию
f(x) =.xsin —,  х ln 2 2х
х ln 2 2х
2. Найти производные следующих функций: 

3.  Для функции у оп редел ить левую и правую производные в sinx 2 точке х = 0, если у =
Для функции у оп редел ить левую и правую производные в sinx 2 точке х = 0, если у =
4. Найти у, если у = sinx +cosx.
5. Найти уравнение той касательной к параболе у 2 = 20х, которая образует угол 45 0 с осью ОХ.
6. Найти предел функции, используя фактор скорости роста
функции 1im 
7. Найти, используя любой прием, предел фунщии  х+е -1
х+е -1
lim 
— 0 3х — 4sinx — arctgx
8. Разложить в ряд Маклорена функцию у = е 2 до 4) 
хз
9. Найти асимптоты кривой у = 
10. Исследовать функцию и по результатам исследования построить ее график у = 
 Вариант 2
Вариант 2
1. Исследовать на непрерывность в точке х = 1 функцию f(x) = 
2. Найти производные следующих функций, предполагая, что они существуют: у = 3.Jiiiii COS 2х 
3. для функции определить левую и правую производные в
х 2 sin—, х;е0, точке х = 0, если у =х
4. Найти о), если у = sin2x.
5. Найти уравнения касательных к окружности х 2 + у 2 = 52, параллельных прямой 2х + Зу = 6.
6. Найти предел функции, используя правило Лопиталя

7. Найти, используя любой прием, предел функции
lim 
8. Разложить в ряд Маклорена функцию у = е2—3х до 4).
9. Найти асимптоты кривой у = х 2 —1.
х
10. Исследовать функцию у = и по результатам исследования построить ее график.
Вариат З
1. Исследовать на непрерывность в точке х = 0 функцию f(x) = xln 2 х, х * 0, ЛО) = а.
2. Найти производные следующих функций, предполагая,
 2х-5
2х-5
что они существуют: ln cos
1—х,
3. Для фундии у определить левую и правую производные в
Х
точке х = 0, если у = arcsin 
4. Найти, если у = 
 — 2х
— 2х
5. Найти уравнение касательной к окружности х а + у2  —2х + 4у — 3 = 0 в точках пересечения ее с осью ОХ.
—2х + 4у — 3 = 0 в точках пересечения ее с осью ОХ.
6. Найти, используя фактор скорости роста функции, предел функции lim 
7. Найти, используя любой прием, предел функции
ln (е- 2х + sin 2х)
lim 
 sin 2 2х
sin 2 2х
8. Разложить в ряд Маклорена функцию у = ех +е-х до о(хб 
9. Найти асимптоты кривой у = з х з — х2 
10. Исследовать функцию у = Glnx и по результатам исследования построить ее график.
Вариант 4
1. Исследовать на непрерывность функщию
f(x) = 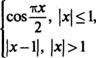
пострбив ее график.
2. Найти производные следующих функций, предполагая, что они существуют: у = sinx. tg2x•cosx, у = ln(u(x)v(x)).
3. Для функции определить левую и правую производные в точке х = 0, если 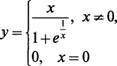
4. Пусть и(х) иу(х) дважды дифференцируемые функции. Найти Гу, если у u(x)v(x).
5. Найти уравнения касательных к гиперболе 4х2 —9у2 = 36, перпендикулярных к прямой 2у + 5х = 10.
6. Найти, используя правило Лопиталя, предел функции

7. Найти, используя любой прием, предел функции
arctg х lim

8. Разложить в ряд Маклорена фуню.щю у = е- до о(хб ).
9. Найти асимптоты кривой у = 
6х 2 — х 4
10. Исследовать функцию у = и по результатам ис9 следования построить ее график.
Письменный экзамен
Продолжительность экзамена 120 мин. Оценивание задач:  — 2 балла, 5, 9,10 — 4 балла.
— 2 балла, 5, 9,10 — 4 балла.
Вариант 1
1. Бесконечно малые функции. Символ «о»-малое, его свойства (без доказательства). Основные асимптотические равенства.
2. Первое достаточное условие локального экстремума (с доказательством).
3. Доказать, что впо| Уп  loga п < пк
loga п < пк 
19 Математический анализ
О
4. Сформулировать с помощью кванторов следующее утверждение: lim f(x) = Ь и изобразить графически функцию вблизи левой оКрестности точки х = а.
5. Найти пределы:

6. Привести (в аналитическом и графическом виде) пример функции у(х), имеющей в точке разрыва х = хо бесконечную производную. Обосновать.
7. Доказать, ЧТО (ха = су•ха 
8. Найти угол, образуемый ветвями функции у = 1—2х1 в точ-

9. На одной координатной плоскости построить график функции f(x), на котором будут отражены следующие ее свойства: 1)f(x) определена и непрерывна при.xeR; 2)  f(x)
f(x)
3) lim = 1; 4) lim f'(x) = +00; 5) lim f(x)=l.
Х +00 х
10. Построить график фуню.щи у = sgn (cosx) на отрезке
lxl 
Вариант 2
1. Теорема о существовании предела у монотонной ограниченной последовательности (с доказательством).
2. Понятие ВЫПУКЛОСТИ функции. Теорема об условиях выпук.ЛОсти функции (с доказательством).
3. Пусть последовательность.хп ограничена, а последовательностьуп не ограничена. Что можно утверждать о последовательности хл + уп? Привести примеры.
4. Доказать, что arcsin = х+о(х) при х 0.
5. Найти пределы:
1) lim Оп х— х);

3 274х- 3 27-х
2)  lim
lim
6. Используя определение производной, найти производную функции в произвольной точке.
7.  Можно ли утверждать, что сумма двух функций не имеет конечную производную в точке, если одна функция имеет конечнуто производную в этой точке, а другая не имеет ее? Привести примеры.
Можно ли утверждать, что сумма двух функций не имеет конечную производную в точке, если одна функция имеет конечнуто производную в этой точке, а другая не имеет ее? Привести примеры.
8. Найти угол, образуемый ветвями функции у = в
точке х = З.
9.
 |
Пусть фуню.щя у = f(x) определена при х > 0. Положим М(х) = sup. Построить график функции у = М(х), если f(x) = sinx, т.е. построить график фунщии у(х) = sup sin(.
10. Исследовать функцию и построить ее график (найти промежутки непрерывности, монотонности, выпуклости, асимптоты, экстремумы и т.д.): у = 
Вариант З

1. Теорема об ограниченности сходящейся последовательности (с доказательством).
2. Теорема Ролля (с доказательством).
3. Пусть последовательности хп и уп расходятся. Что можно
утверждать о последовательности.xnyn? Привести примеры.
4. Доказать, что sinx = х+о(х) при х 0.
5. Найти пределы:
1) lim(cos log2 cosx);
З

 .
.
6. Используя определение производной, найти по определе-
нию производную функции у = в произвольной точке.
1—х
7. Можно ли утверждать, что сумма двух фующий не имеет конечную производную в точке, если обе фующии не имеют конечную производную в рассматриваемой точке? Привести примеры.
8. Найти угол, образуемый ветвями функции у =  в точке х = 8.
в точке х = 8.
9. При каком а функция у =.х2 +а наименее «отклоняется от нуля» на отрезке [— 1, 1], т.е. выполнено условие  = min?
= min? 
 10. Исследовать фунщию у = хз —3х (найти промежутки непрерывности, монотонности, выпуклости, асимптоты, экстреМУЫи т.д.) и построить ее график.
10. Исследовать фунщию у = хз —3х (найти промежутки непрерывности, монотонности, выпуклости, асимптоты, экстреМУЫи т.д.) и построить ее график.
Вариат 4
1. Первый замечательный предел (с обоснованием).
2. Касательная к кривой. Вывод уравнения касательной.
3. Даны последовательности: {х а) уп; б) (—;

Имеются утверждения:1) УЕ > 0, Упо,Зп >nol <;

Составить и заполнить таблицу истинности.
| Утверждение | Последовательности | ||
| а | |||
4. Сформулировать с помощью кванторов следующие утверпения: lim Лх) = —оо, limf(x) = Ь.
5. Вычислить: 1) lim х2х 3 ,
I — cos4x
2) lim 2 
х sin х + cosx—l
3) lim 2
х
cos(a + 2х) — 2 cos(a + х) + cosa 4) lim 
6. Найти производные у', если: у = sin3x•cos 2 х, у =.
7. Найти правый и левый пределы функции lim logx 2.
8. Разложить в ряд Маклорена функцию у = е sin х до о (х4).
9. Найти sup l—x2 +3х+41.
10. Построить на одной координатной плоскости график функции, определенной при х е R, на котором будут отражены следующие соотношения:
 —2, lim f'(x) = —оо, lim f'(x) = +00, lim f'(x) = 0, lim f(x) —
—2, lim f'(x) = —оо, lim f'(x) = +00, lim f'(x) = 0, lim f(x) — 
Оценка за семестр выставляется по формуле (см. симабус).
Вопросы для оценивания порогового уровня знаний студента в комиссии
Каждый пункт — балл. Условие сдачи экзамена — 15 баллов
1. Сформулировать определение сходящейся последовательности.
2. Может ли сходящаяся последовательность быть неограниченной? Обосновать.
3. Что такое полярные координаты. Привести пример функции, заданной в полярных координатах.
4. Сформулировать определение предела функции в точке.
5. Сформулировать с помощью кванторов следующее утверждение: lim f(x) = Ь. 
6. Привести пример функции, бесконечно малой в окрестности точки х = З.
Найти: tgx + 2х
7. lim
8. lim 1—— 
sin х
9. lim 
10. 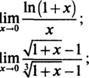 1im
1im
11. lim
12. lim х—! tgx
2 arctg 2х
13. hm
—0 arcsin 3х
14. Сформулировать определение непрерывности функции в точке.
15. Может ли функция, определенная на отрезке, не достигать своего наименьшего или наибольшего значения?
16. Сформулировать определение производной функции в точке.
Найти производные функций:
1 17. у = ctg2x+arcctg—,
х
18. f2 (из (х)).
19. Найти производную функции у у(х), заданной неявно: х2 + у2 + х2у2 = 1,
20. Найти производную х:, если у х + ln х.
21. Привести (в аналитическом и графическом виде) пример непрерывной функции, не имеющей производную в точке хо.
22. Какая функция называется дифференцируемой в точке?
23. Что такое дифференциал функции? Аргумента? и(х) 24. Чему равен d  v(x)
v(x)
25. Объяснить геометрический смысл производной.
26. Разложить функцию е2х в ряд Маклорена до о (х5).
27. Привести пример функции, имеющей три вертикальные асимптоты.
28. рдля фунющи дать определение выпуклости, направленной вверх.
29. Сформулировать определение точки перегиба.
30—31. Построить фрагмент графика функции в окрестности точки хо, если f+' (хо) = = +00.
 32. Найти уравнение касательной к параболе у = Л в точке с абсциссой хо = 4.
32. Найти уравнение касательной к параболе у = Л в точке с абсциссой хо = 4.
33—34. Построить фрагмент графика функции в окрестности точки хо, если (хо) = = — 
На одной координатной плоскости нарисовать график функции f(x), на котором будут отражены свойства функции:
35. lim 
36. lim f(x)=+oo;
37. lim f(x)= 
 .
.
39—45. Исследовать (найти промежутки непрерывности, монотонности, выпуклости, асимптоты, экстремумы) функцию у = (х —1) (х — 2)(х —3) и построить ее график.
Контрольная работа N 2 •3
Оценивание задач: 1--10 — 2 балла. Длительность: 90 мин.
Вариант 1
1. Доказать, что
| а2 и | д2 и д2и | д2и | |
| ар | 0х 2 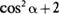 дхду дхду   
| 
| —=cos2 $, Ду |
где а, $ -- углы между направлением I и осями координат ОХ и ОУ.
2. Построить фрагмент карты линий уровня Z max(lxl,lyl) 
2х
3. Найти двойной предел lim, если он существует.

4. Привести пример с обоснованием функции двух переменных, у которой существует конечный предел по любому направлению, но просто предела нет.
5. Исследовать функцию на дифференцируемость в точке

6. Найти дифференциал 2-го порядка от функции:

7. Выписать в развернутом виде третий дифференциал функции двух переменных. dtl
8. Найти если: и U(sin у(х), cosy(x)) dx
9. Для функции z  на координатной плоскости укаху
на координатной плоскости укаху
зать множество точек, в которых направление градиента имеет
 угол, удовлетворяющий условию 0 < < —.
угол, удовлетворяющий условию 0 < < —.
Ш. Функции и и у переменных х и у заданы неявно системой  Найти И:, Ы., у:, v'
Найти И:, Ы., у:, v' 
Вариант 2
1. Доказать, что =(gradf, l), где  — производная по
— производная по
направлению, — единичный вектор.
2. Построить фрагмент карты линий уровня Z = min(x2 , у).
3. Найти двойной предел lim  если он существует.
если он существует.
4. Привести пример с обоснованием функции двух переменных, которая непрерывна в точке по бесконечному числу направлений и которая разрывна в этой точке.
5. Исследовать функцию на дифференцируемость в точке Р(о, О): 
6. Найти дифференциал 2-го порядка от функции

7. Выписать в развернутом виде 2-й дифференциал функции трех переменных. du
8. Найти dx ' если: х, х— у(х)).
 9. На координатной плоскости указать множество точек, в которых градиенты функций 4 = sinx—2cosy и cosx + cosy коллинеарны.
9. На координатной плоскости указать множество точек, в которых градиенты функций 4 = sinx—2cosy и cosx + cosy коллинеарны.
10. Пусть х = = z(u,v) определяют z как
 функцию от х и у. Найти
функцию от х и у. Найти
дх' ду
Вариант З
1. Доказать, что тах |gradfl, где  — производная по направлению.
— производная по направлению.
2. Изобразить фрагмент карты линий уровня функции х

3. Привести пример в аналитическом виде функции двух переменных и(х, у), у которой обе частные производные в некоторой точке их (хо,уо) и и: (хо,уо) обращаются в бесконечность, причем и: (хо,уо)=—оо, и: 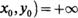 .
.
4. Построить фрагмент карты линий уровня  3х2), 20, х) >O.
3х2), 20, х) >O.
5. По каким направлениям существует конечный предел
lim е х +Ј', если x=pcosp, y=psinp?
6. Исследовать функцию на дифференцируемость в точке Р(О, О): 
7. Найти дифференциал 2-го порядка от функции: и = xyz.
8. Найти —, если:  dx
dx
9. На координатной плоскости указать точки, в которых градиенты функций 4 х +у2 и Ъ х2 + у противоположны по направлению.
Ш. Пусть х = x(u,V), у = Найти частные производные от обратных функций: и = и(х,у) и = v(x,y).
Вариант 4
1. Доказать, что касательная к линии уровня функции двух переменных ортогональна градиенту этой функции.
2. Найти двойной предел lim  если он существует.
если он существует.
3. Привести пример и обосновть в аналитическом виде функции двух переменных и(х,у), у которой обе частные производные в некоторой точке их (хо,уо) и иу (хо,уо) равны +00.
4. Построить фрагмент карты линий уровня у = тах(Зх,; 2х2),  > 0.
> 0.
5. По каким направлениям существует конечный предел
lim ех У , если.x=pcosp, y=psinp?
6. Исследовать функцию f(x, у) на дифференцируемость в точке Р (0, 0).
7. Найти дифференциал 2-го порядка от функции

8. Найти, если и = и(у2 (х), х2 ) 
9. В какоћаправлении нужно выйти из точки (l,l), чтобы
функция фхУ2у-У2 не изменилась (указать соответствующие углы)?
10. Найти, если  •
•
ДхРДјВ
Контрольная работа № 4
Оценивание задач: 1—4, 6—10 — 2 балла, 5 — 8 баллов, длительность: 90 мин.
Вариант 1
1. Перечислить свойства определенного интеграла.
2. Найти у = у(х) из уравнения: xdx+y2dy = 0.
3. Из совокупности всех первообразных у(х) = f2xdx выбрать те, графики которых касаются окружности х) + =.
 4. Можно ли в интеграле fF7d.x при замене перемен-
4. Можно ли в интеграле fF7d.x при замене перемен-
ной х = 2sint в качестве новых пределов взять числа 0 и 2,5т? Обосновать ответ.
5. Найти:
З

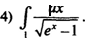
6.  Вычислить: sintdt
Вычислить: sintdt
dx2
7.  Оценить интеграл:
Оценить интеграл:
8.  Найти площадь фигуры: х2 + х —2 < у < —. 4
Найти площадь фигуры: х2 + х —2 < у < —. 4
9. Вычислить несобственный интеграл или установить его расходимость.
10. Исследовать сходимость интеграла:
Вариант 2

1. Привести определение среднего значения функции на отрезке. dy
2. Найти у=у(х) из уравнения cosxdx=если
 1-у2
1-у2
3. Для каждого значения постоянной интегрирования С определить число решений уравнения: cosxdx=O на отрезке

4. Каким условиям должен удоњлетворять параметр а, чтобы в интеграле.fJ6idx можно было сделать замену х = sint?
5. Найти:
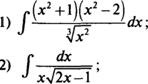
3) J4xcos2xdx;
 -1
-1
cosx2dx
7. Найти lim 0

8.Найти площадь фигуры elxl lyl е
9. 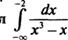 Вычислить несобственный интегралили установить его расходимость.
Вычислить несобственный интегралили установить его расходимость.
cosx
10. Исследовать сходимость интеграла: dx.
Вариат З
1. Сформулировать 1-ю теорему сравнения для несобственных интегралов 1-го рода.
2. Из совокупности всех первообразных у(х) = Г (х +l)dx выбрать те из них, которые не пересекают ось Х.
3. Доказать, что если f(x) — непрерывная периодическая
функция с периодом Т, то
4.  Найти производную функции: F(x)=
Найти производную функции: F(x)=
5. Найти: sinx
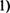 —dx;
—dx;
 dx; 3) fx2 cosxdx;
dx; 3) fx2 cosxdx;
4) TfJiiGidx.
 2
2
6. Найти 
7. Доказать, что если  F(x)+C, то ff(ax + b)dx = — F(ax + Ь) + С.
F(x)+C, то ff(ax + b)dx = — F(ax + Ь) + С.
О
8. Найти площадь фигуры, ограниченной линиями у = sinx, y=arctgx в области О<х<—, считая абсциссу од-
ной из точек пересечения равной хо = — (фактически хо 1,56).
9.  Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
10. Исследовать сходимость интеграла:
Вариант 4
1. Сформулировать 1-ю теорему сравнения для несобственных интегралов 2-го рода.
2.  Решить уравнение
Решить уравнение  dx, зная, что
dx, зная, что  ,
,
3. При каких значениях постоянной интегрирования С уравнение Г (2х— l)dx = I имеет ровно одно решение?
4.  Найти производную функции: Е (х) =cos t2dt.
Найти производную функции: Е (х) =cos t2dt.
5. Найти: 
 dx;
dx;
3) f$dx 
 2
2
заключен между — и
 Найти точное значение интеграла.
Найти точное значение интеграла.
8. Найти площадь фигуры lyl —lnlxl,
9.  Вычислить несобственный интеграл 2 dx или установить его расходимость.
Вычислить несобственный интеграл 2 dx или установить его расходимость.
10. Исследовать сходимость интеграла:
Экзаменационная работа
Оценивание задач: 1—7, 9—10 — 2 балла, 8 — 8 баллов. Длительность экзамена: 120 мин.
Вариант 1
1. Дифференциалы высших порядков. Случаи независимых и зависимых переменных.
2. Сформулировать и доказать 1-ю теорему сравнения для несобственных интегралов 1-го рода.
3. Построить область. D =  у = eix
у = eix 
и вычислить ее площадь, используя двойные интегралы.
4. Упростить выражение (Е Х (А u (Е \ u (В п (Е \ В)).
5. Вычислить 
6. Найти производную функции и = х2 — ху в точке (1, 1) по направлению [, задаваемому утлом (У, и построить эпюру Ди
 Указать направления, по которым функция имеет
Указать направления, по которым функция имеет
наибольшее изменение.
7. Построить на координатной плоскости фрагмент карты градиентов функции и для > 0, х2 > 0, если и = +х2.
8. Найти интеграл:

2) fcos4 xdx;
О
3) Г 2 —х2 +2x+ldx;
4) г Х4 — 6Х3 -4-12Х2 6 dx.
Ј хз —6х2 +12х—8
9. Найти площадь фигуры, которая задается на координатной плоскости условиями: cosx < у < sinx, 0 < х < —.
10.  Вычислить несобственный интегралили установить расходимость.
Вычислить несобственный интегралили установить расходимость.
Вариант 2
1. Формула Ньютона—Лейбница (с выводом).
2. Понятие двойного интеграла. Основные свойства двойно-
го интеграла.
3. Построить область D = х2 —lxl S l—x2 и вычислить
ее площадь, используя двойные интегралы.
4. Упростить выражение \ А) U В) п ((Е \ А) U (Е \ В)).
5. Вычислить (1 +i)10 
6. Построить на координатной плоскости фрагмент карты градиентов функции И=Х1 —х2 для > 0, х) > 0.
7. Найти производную функции и = C2x 12 yY2 в точке (1, 1)
по направлению, задаваемому углом, и построить эпюру ди 
 = Указать направления, по которым функция имеет
= Указать направления, по которым функция имеет
 наибольшее изменение. 8. Найти интегралы: 1) 15. з (3x+5)2 dx;
наибольшее изменение. 8. Найти интегралы: 1) 15. з (3x+5)2 dx;
6х2
 —dx;
—dx;

9. Найти площади двух замкнутых фигур, которые образу-
ются при пересечении фунюдий у arcsinx и у = 2 х 2 , считая 2
 абсциссу одной из точек пересечения равной хо — — (фактически хо х 0,71).
абсциссу одной из точек пересечения равной хо — — (фактически хо х 0,71).
10. Вычислить несобственный интегралили установить расходимость.
Вариант З
1. Понятие несобственного интеграла 1-го рода. Эталонный интеграл 1-го рода.
2. Булева алгебра. Операции над элементами. Таблица истинности.
3.  Построить 1) = < min(tgx, ctgx), О <х<— об2 ласть и вычислить ее площадь, используя двойные интегралы.
Построить 1) = < min(tgx, ctgx), О <х<— об2 ласть и вычислить ее площадь, используя двойные интегралы.
4. Упростить выражение

6. Найти угол между градиентами функции Z = ln— в точках
 0,25) и ВО, 1). х
0,25) и ВО, 1). х
7. Построить на координатной плоскости фрагмент карты градиентов функции и = для.Xl > 0, Х2 > 0.
8. Найти интегралы:
 dx.
dx.
9.  Найти площадь фигуры, которая задается на координатной плоскости условиями: 2х < у < 2х.
Найти площадь фигуры, которая задается на координатной плоскости условиями: 2х < у < 2х.
10. Вычислить несобственные интегралыили установить их расходимость.
Вариант 4
1. Понятие неопределенного интеграла, его свойства (с обоснованием).
2. Показательная форма комплексного числа, формула
Эйлера (с выводом).
З. Построить область D = —<у<—, 10 5 и вычислить
Х х
ее площадь, используя двойные интегралы:.
4. Доказать равенство А Х С) = (А \ В) U (А п С).
5. Решить уравнение —8i 0.
6. Построить на координатной плоскости фрагмент карты градиентов функции и для х) > О, х2 > 0, если и = х: + х2.
7. Учитывая непрерывность первообразной, найти интеграл: flxldx 
8. Найти интеграл:
1) ——dx 3х+4;
Ј 3х+2
2) fcos5 xdx;

9. Найти площадь фигуры, ограниченной линиями
у = sinx, y=arctgx в области 0 < х < —, считая абсциссу одной
ТГ
из точек пересечения равной хо — (фактически хо z 1,56).
10. Вычислить несобственный интеграл или установить расходимость. 0
Вопросы для оценивания порогового уровня знаний студента в комиссии
Каждый пункт — 1 балл.
Условие сдачи экзамена — 15 баллов
1. Сформулировать определение линии уровня функции двух аргументов.
2. Какая фунющя двух переменных называется дифференцируемой?
3. Сформулировать определение дифференциала функции трех аргументов.
4. Сформулировать определение производной по направлению. По какой формуле вычисляется производная по направлению?
5. Что называется градиентом функции? Как направлен градиент по отношению к линии уровня функции?
6. Нарисовать фрагмент карты, линий уровня функции
7. 

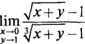 Найти двойной предел lim или доказать, что он не существует.
Найти двойной предел lim или доказать, что он не существует.
8. Найти частные производные 1-го и 2-го порядков функции z 4х2 + зуз +2х2уз +1.
9. Найти частную производную — и полную производную du дх — функции и = sinxy, где у = у(х). dx
10. Выписать в развернутом виде дифференциал 2-го порядка функции четырех переменных.
11. Найти частные производные функции Z = z(x, у), заданной неявно: 3х 2 — 2ху + Z 2 +yz—l = 0.
12. Найти дифференциал 2-го порядка от функции, считая аргументы независимыми переменными и = —. du
13. Найти, если и = х = (Ш), у = f3(t). dt
14. Найти ух функции у = у(х), заданной неявно:

15. Разложить по формуле Маклорена до членов 3-го порядка включительно функцию Z = sin 2х + cos3x.
16. Что называется неопределенным интегралом от фуню.щи? 17—23. Найти неопределенный интеграл.

 , —и fJiGidx,
, —и fJiGidx,
х
24. Найти у = у(х) из уравнения d(lny)+dx=O, если

25. Зная величину производной функции, определить вид функциональной зависимости.у' = 2.
26. Что называется средним значением функции на отрезке?
27. Найти производную функции F(x) = lntdt, х > 0.
28. Оценить интеграл 
29. Найти площадь фигуры, ограниченной линиями У = З+2Х—Х2 , у.
30. Что называется несобственным интегралом 1-го рода?
31. Доказать, что эталонный несобственный интеграл 2-го рода — сходится при р < и расходится при р >.
32—33. Вычислить несобственный интеграл или установить его расходимость е-ХИ, cosxdx.
 34—35. Исследовать сходимость интегралов
34—35. Исследовать сходимость интегралов 
Список литературы
1. Архипов Г.И., СаДОВНИЧИЙ В.А., Чубариков В.Н. Лекции по математическому анализу. — М.: Высшая школа, 1999.
2. КуДрявцев Л.Д. Краткий курс математического анализа (в 2-х тт.). — М.: АЛЬФА, 1998.
3. Ильин В.А., Позняк ЭМ. Основы математического анализа. — М.: Наука. 1995.
4. Краснов М.Л. и др. Высшая математика (тома 1, 2, 4). — М.: Едиториал УРСС, 2000.
5. Высшая математика для экономистов / Под ред. Н.Ш.Кремера. — М.: Юнит, Банки и биржи, 1998.
6. Ляшко И.И., Боярчук А.К., Гай Я.Г., Гловач ГЛ. Справочное пособие по высшей математике (том 1). — М.: Едиториал УРСС, 1995.
7. Красс МС. Математика для экономических специальностей. — М.: ДЕЛО, 2002.