Математическая модель для определения ПКН

МЕТОД ОПРЕДЕЛЕНИЯ

ПРОЕКТНО-КОНСТРУКТОРСКОГО НОРМАТИВА (ПКН)

 

Математическая модель для определения ПКН

 

Чтобы лучше понять формализацию задачи, рассмотрим для простоты и наглядности случаи покупки стульев одного типа в мебельном магазине. Логично предположить, что покупатели представляют собой случайную величину нагрузки, распределенную по некоторому закону. Стулья обладают прочностью, которая тоже является случайной величиной, распределенной по своему закону. Обозначим x_н - случайную величину нагрузки, x_n - случайную величину прочности. Тогда графическая модель совместимости нагрузочных свойств покупателей с прочностными свойствами стульев можно представить так, как показано на рис.1.

f(x_n) Щуплый покупатель

f(x_н) Упитанный покупатель

x_н

x_n

 

 

x_n, x_н

Рис.1

 

Допустим, в магазин приходит щуплый покупатель (рис.1) и хочет купить стул из множества имеющихся в магазине. Затем входит упитанный покупатель и тоже хочет купить стул. Можно ли по этой модели оценить риск каждого из покупателей? Как это сделать? Но более актуальна другая постановка задачи: мебельная фабрика предполагает выпуск стульев с металлическими ножками. Каким должно быть сечение металлопрофиля (проектно-конструкторский норматив ПКН) для ножек, чтобы вероятность безотказной работы стульев для пользователей была бы не менее заданной? Или какой разброс сечения профиля ножек стульев допустим, если среднее значение сечения и требуемая вероятность безотказной работы известны?

Разумеется, рассмотренный пример взят для облегчения понимания задачи. В такой постановке существует множество технических задач ЭМС (например, ПКН уровня среза избыточного напряжения атмосферного или коммутационного происхождения средствами защиты, совместимых с заданной вероятностью со случайной величиной амплитуды питающего напряжения и со случайной величиной стойкости изоляции в электротехнических установках, и т.п.).

 

В общем случае вероятность безотказной работы Р объекта со случайной величиной прочности х_п при случайной величине нагрузки x_н можно найти, опираясь на рис.1, по следующим очевидным условиям:

Р=Р(х_п>х_н) или Р=Р(х_п-х_н) >0. (1)

 

Это базовые неравенства, отражающие здравый смысл. Рассмотрим более подробно область пересечений плотностей, где возможна несовместимость х_п и х_н (рис.2).

 

f(x_n) x_н

f(x_н)

x_n

f(x₀)

 

 

x_n, x_н

x₀ dx

 

 

Рис.2

 

 

Ответим на следующие вопросы:

1. Какова вероятность того, что СВ x_н попадет на интервал dx? Ответ будет таким:

 

Р (x₀ - < x_н < x₀ - ) = f(x₀)dx.

 

2. Следующий вопрос такой: какова вероятность того, что х_п>х₀? Очевидно, эта вероятность равна площади под кривой плотности распределения СВ х_п от значения х₀ до ∞:

Р(х_п>х₀)= 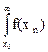dx_n.

3. Очередной, третий, вопрос такой: какова вероятность того, что СВ x_н попадет на интервал dx, и при этом х_п>х₀? Ответ очевидный: имеет место произведение вероятностей:

 

(f(x₀)dx) х (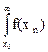 dx_n.).

4. Тогда формула определения вероятности того, что х_п>х_н для всех х_н, получает следующий вид:

Р(х_п>х_н)= 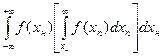. (2)

В практических задачах, в соответствии с центральной предельной теоремой, функции f(х_н) и f(х_п) представляют собой нормально распределенные плотности случайных величин нагрузки и прочности. Рассмотрим решение уравнения (2) для этого случая.

Итак,

f(х_н)= 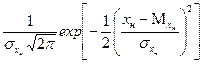, -∞< х_н<∞;

 

f(х_п)= , 0< х_п<∞.

Здесь σ_хн, σ_{хп –} среднеквадратические отклонения случайных величин нагрузки и прочности, М _хн, М _хп – их математические ожидания.

Введем новую случайную величину

у=х_п - х_н.

Известно, что если обе случайные величины х_п - х_н распределены нормально, то и разность между ними тоже имеет нормальное распределение. Следовательно,

f(у)= 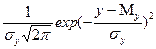, - ∞ < у<∞.

При этом

М _у = М _хп - М _хн,

σ_у =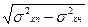

Тогда

Р(х_п>х_н)= Р(у>0)= 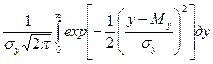. (3)

 

Графическое отображение математической модели (3) имеет вид:

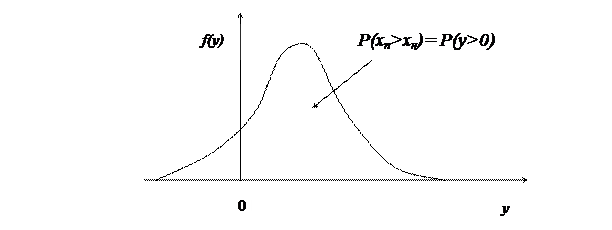
Рис.3

 

Данная графическая модель позволяет зрительно оценить вероятность безотказной работы совмещаемых элементов (по модели на рис.1 такая оценка затруднительна). Однако определить значение ПКН из кравнения (3) также затруднительно. Поэтому введем новую переменную в уравнении (3):

 

z = . (4)

Дифференцируя это уравнение, получаем связь ду и д z:

д z 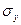= ду.

Определим новые пределы интегрирования.

При у=0 из уравнения (4) находим

z = .

При у=∞ очевидно z =∞.

Подставляя в уравнение (3) найденные значения, получим:

 

Р(х_п>х_н)= Р(у>0)=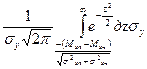

Вынося за знак интеграла 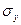и выполнив сокращение, окончательно получим:

 

Р(х_п>х_н)= Р(у>0)= 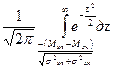. (5)

Важной особенностью математической модели (5) является нормированная нормальная форма, т.к. z = есть нормированная случайная величина, распределенная по нормальному закону. Следовательно, величину Р(х_п>х_н) можно найти с помощью таблиц функции нормального распределения, имеющихся в учебниках по теории вероятностей.

Соотношение z = 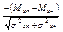, представляющее нижний предел интегрирования, называется уравнением связи. Тогда формулу (5) можно записать в следующем виде:

Р=Р(х_п>х_н) = 1 – Ф(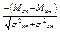). (6)

 

Рассмотрим пример применения математической модели (6) для определения ПКН.

Допустим, известно, что электрическая стойкость (прочность, противодействие перенапряжению) x_п элемента к перенапряжениям и перенапряжения (электрическая нагрузка для элемента) x_н имеют нормальные распределения с параметрами m_xн = 300 В, σ_xн= 30 В и m_xп = 400 В, σ_xп = 40 В. Задан вероятностный норматив Р =0,9772. Требуется определить, до какого среднего уровня следует ограничить перенапряжение (электрическую нагрузка для элемента) x_н, если защитное средство имеет нормально распределенный порог ограничения с σ_xн = 0,1 m_xн. По смыслу задачи искомая величина m_xн и есть ПКН защитного средства.

По таблице для нормального распределения (например, Вентцель Е.С. Теория вероятностей. - М.: Академия, 2003. - 576 с.) находим для Р = Ф^*(х)=0,9772 значение х = 2.

Используя уравнение (6), имеем:

2 = | |.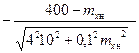

Преобразуя, получаем неприведенное квадратное уравнение

откуда m_xн =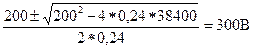

(значение второго корня решения уравнения m_xн = 533,3 В лишено здравого смысла, поскольку заведомо превышает средний уровень стойкости (противодействия) элемента).

Литература

1. Костроминов А.М. Защита устройств железнодорожной автоматики и телемеха­ники от помех. - М.: Транспорт, 1995. - 192 с.

2. Вентцель Е.С. Теория вероятностей. – М., Академия, 2003. - 576 с.