ЭДС, наводимые в обмотках машин переменного тока, характеризуются тремя основными параметрами: величиной, частотой и формой кривой. Обычно требуется, чтобы ЭДС была практически синусоидальной. Особенно это относится к генераторам, так как высшие гармонические оказывают на все элементы электрических сетей вредное влияние.
Рассмотрим вопрос об ЭДС обмоток машин переменного тока на примере синхронного генератора.
ЭДС, НАВОДИМАЯ В ПРОВОДНИКЕ
Будем рассматривать один проводник обмотки якоря 2, который расположен в пазу на внутренней поверхности сердечника статора 1 синхронного генератора, как это изображено на рис. 6.3. Ротор 3 с обмоткой возбуждения представляет собой электромагнит. Он вращается первичным двигателем с частотой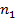 
в направлении указанном стрелкой.
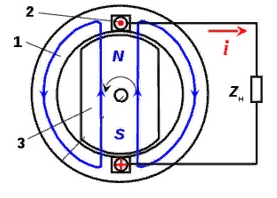
Рисунок 6.3. Упрощенная модель синхронного генератора
В рассматриваемом проводнике обмотки якоря индуктируется ЭДС, направление которой определяется правилом правой руки, а мгновенное ее значение равно
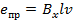(6.5)
где 
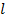и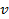 
- активная длина и скорость движения магнитного поля;
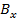- индукция в месте нахождения проводника в данный момент времени.
Так как 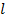и 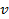обычно постоянны, то закон изменения ЭДС во времени (т.е. форма кривой) точно соответствует кривой распределения индукции в воздушном зазоре вдоль внутренней окружности сердечника статора. Чтобы сделать кривую ЭДС синусоидальной, необходимо создать магнитное поле, распределяющееся в воздушном зазоре по синусоидальному закону.
Если индукция в воздушном зазоре изменяется по синусоидальному закону, то величину ЭДС можно определить следующим образом:
Окружную скорость вращения магнитного поля можно записать в виде
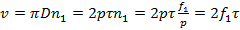(6.6)
где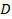 
– внутренний диаметр сердечника статора;
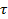- полюсное деление.
Для синусоиды можно записать
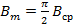(6.7)
Тогда максимальное значение ЭДС в проводнике будет равно
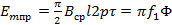(6.8)
где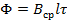 
- полный магнитный поток одного полюса.
Действующее значение ЭДС
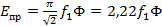(6.9)
Однако индукция в воздушном зазоре часто изменяется по закону отличному от синусоидального. В этом случае кривую индукции можно разложить в гармонический ряд. Она содержит обычно лишь нечетные гармоники ввиду симметрии кривой относительно оси полюсов ротора. Каждая из гармоник поля будет индуктировать свою ЭДС и действующее значение результирующей ЭДС будет равно
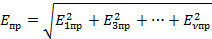(6.10)
где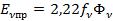 
- ЭДС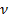 
-той гармоники; 
; 
.
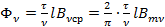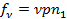Из (6.10) следует, что высшие гармонические мало влияют на величину ЭДС, но могут сильно исказить синусоидальность ее формы.
ЭДС ВИТКА, ЭДС КАТУШКИ
Обмотки машин переменного тока, также как и якорные обмотки машин постоянного тока, состоят из катушек. Каждая катушка состоит из одного или нескольких витков. Ширина катушки определяется шагом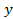 
(рис. 6.4).
Если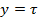 
, обмотка называется с полным или диаметральным шагом. При 
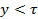- обмотка с укороченным шагом. Обмотки с удлиненным шагом (
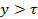) практически не применяются. Обмотки машин переменного тока чаще всего выполняются с укороченным шагом.
Отношение шага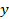 
к полюсному делению называется относительным шагом обмотки 
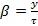. В обмотках с укороченным шагом 
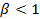. В этом случае виток обмотки будет расположен так, как представлено на рис. 6.4.: одна сторона витка в рассматриваемый момент времени находится на оси северного полюса, а вторая – сдвинута относительно оси южного полюса на расстояние 
.
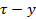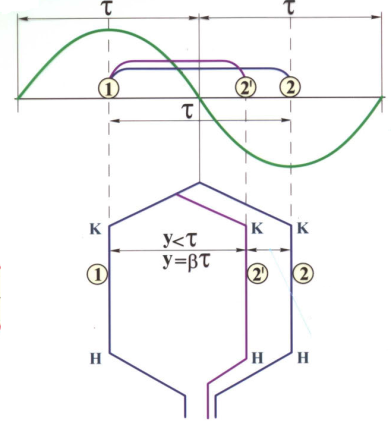
Рисунок 6.4. Укорочение шага обмотки
В теории электрических машин пользуются понятием об электрических градусах. Если индукция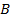 
магнитного поля распределяется вдоль воздушного зазора по синусоидальному закону (рис.6.4), то каждой паре полюсов, т.е. двойному полюсному делению 
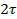, соответствует полная синусоида (
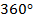или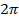 
радиан). Поэтому окружность внутренней поверхности якоря, соответствующая геометрическому углу 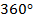в электрическом отношении соответствует углу 
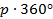, так как вдоль воздушного зазора располагается 
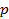полных синусоид, где 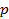– число пар полюсов. Поэтому угол 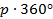называется электрическим. Один геометрический градус равен 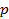электрических градусов. В двухполюсных электрических машинах (
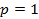) геометрические градусы совпадают с электрическими.
Шагу обмотки 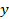соответствует угол 
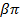. Следовательно, основные гармонические ЭДС в проводниках 
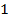и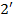 
будут сдвинуты по фазе на этот угол, как это представлено на рис. 6.5.
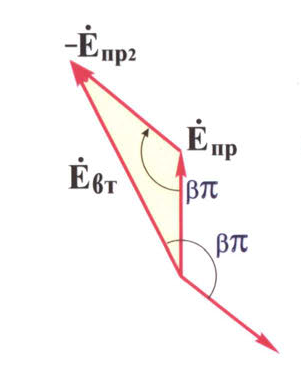
Рисунок 6.5. Векторная диаграмма ЭДС при укорочении шага обмотки
ЭДС витка равна
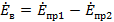(6.11)
или
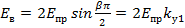(6.12)
где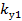 
- коэффициент укорочения шага обмотки для первой гармонической ЭДС
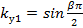(6.13)
Если обмотка выполнена с полным шагом, то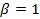 
и 
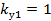. При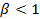 
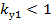, следовательно ЭДС витка с укороченным шагом всегда меньше ЭДС витка с полным шагом. Таким образом, укорачивая шаг обмотки, мы проигрываем по величине ЭДС, но улучшаем форму кривой, приближая ее к синусоиде.
Действительно, период любой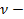 
ой гармоники в 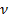раз меньше периода основной гармонической, поэтому шагу обмотки для 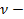ой гармоники соответствует угол 
.
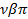Тогда коэффициент укорочения для любой 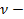ой гармоники равен
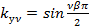(6.14)
Из (6.14) следует, что можно подобрать такое укорочение шага, когда для одной из гармоник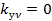 
, т.е. в результирующей кривой ЭДС данная гармоника будет отсутствовать. Например, для уничтожения 5-ой гармоники необходимо выбрать шаг 
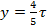, в этом случае 
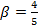, а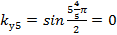 
. Для уничтожения 7-ой гармоники необходимо принять 
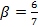и т.д.
Обычно в трехфазных обмотках стремятся уменьшить 5-ю и 7-ю гармоники. В этом случае шаг обмотки выбирают равным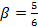 
. Тогда 
; 
.
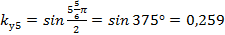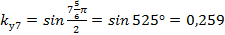Таким образом, эти гармоники уменьшаются практически в четыре раза по сравнению со случаем, когда 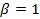, а первая гармоническая ЭДС изменяется незначительно, так как 
..
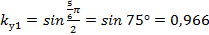Обмотки машин переменного тока выполняются из катушек, каждая из которых состоит из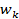 
числа витков.
В этом случае ЭДС катушки определяется по формуле
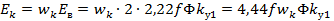(6.15)
ЭДС КАТУШЕЧНОЙ ГРУППЫ
Обычно каждая фаза машин переменного тока выполняется не сосредоточенной, а распределенной, то есть состоит не из одной катушки, а из нескольких, уложенных в разных пазах и соединенных между собой.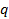 
катушек, имеющих одинаковое число витков 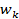, лежащих в соседних пазах и соединенных последовательно называется катушечной группой.
Предположим, что на полюсное деление приходится 4 паза, а фазовая обмотка располагается в 3 пазах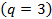 
. Здесь 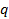– число пазов на полюс и фазу. Схема укладки катушек с полным шагом показана на рис. 6.6.
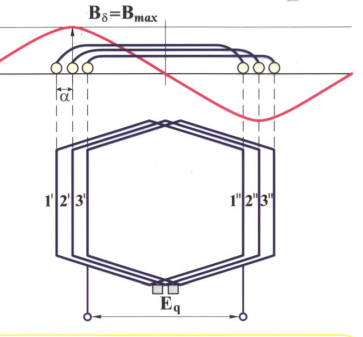
Рисунок 6.6. Схема укладки катушек с полным шагом
Угол сдвига между соседними пазами в электрических градусах равен
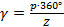(6.16)
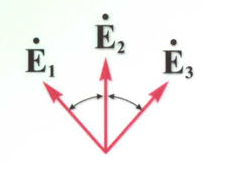
Рисунок 6.7. Векторная диаграмма ЭДС катушечной группы
В рассматриваемом случае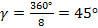 
. На этот угол сдвинуты по фазе ЭДС, индуктируемые в соседних катушках. Векторную диаграмму ЭДС можно изобразить, как это показано на рис.6.7. Так как все катушки соединены последовательно, ЭДС катушечной группы определяется как геометрическая сумма ЭДС отдельных катушек (рис.6.8). Просуммировав векторы 
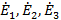, получим часть правильного многоугольника, вписанного в окружность. Вся обмотка из 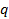катушек занимает по окружности угол 
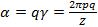, который называется углом фазной зоны.
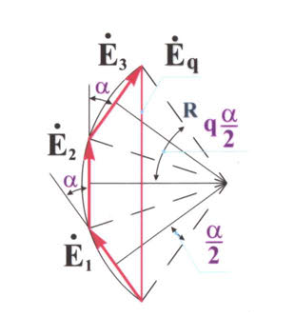
Рисунок 6.8. К определению ЭДС катушечной группы
ЭДС катушечной группы
. 
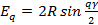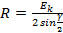(6.17)
Следовательно,
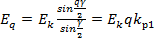(6.18)
где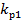 
- коэффициент распределения обмотки для первой гармоники ЭДС.
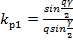(6.19)
В сосредоточенной обмотке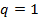 
и 
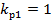. При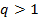 
, 
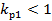, поэтому коэффициент распределения обмотки характеризует уменьшение ЭДС из-за пространственного сдвига катушек по отношению друг к другу.
В общем случае для высших гармоник ЭДС угол между двумя соседними пазами равен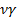 
. Тогда коэффициент распределения для 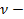ой гармоники
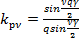(6.20)
При определенном соотношении между 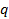и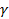 
коэффициент распределения для некоторых гармоник может стать равным нулю. Таким образом, можно утверждать, что применение распределенной обмотки улучшает форму кривой ЭДС.