Этот метод является универсальным, так как им пользуются при построении линий пересечения, как тел вращения, так и многогранников. Сущность метода заключается в следующем:
1. Заданные поверхности пересекают рядом вспомогательных секущих плоскостей-посредников. Это обычно плоскости частного положения, т.е. параллельные какой-либо плоскости проекции, и проводят их так, чтобы заданные поверхности пересекались по графически простым линиям, проецирующимся в виде прямых или окружностей.
2. Вычерчивают фигуры сечений посредника с каждой из заданных поверхностей в отдельности.
3. Находят точки пересечения фигур сечений, которые и принадлежат искомой линии пересечения поверхностей.
При построении точек линии пересечения сначала находят опорные (характерные) точки, т.е. высшую и низшую, крайние правую и левую, определяющие границу видимости проекций линии пересечения. Эти точки показывают, в каких пределах расположены проекции линии пересечения и где между ними целесообразно определять промежуточные точки для более точного построения линии пересечения поверхностей.
Найдя точки линии пересечения, нужно их последовательно соединить с учетом видимости, исходя из следующих положений:
1. Видимость определяют на всех проекциях отдельно.
2. Для кривых поверхностей видимыми являются точки, получающиеся в пересечении двух видимых образующих. Если хотя бы одна из образующих невидима, то и точка линии пересечения невидима.
3. Точки перехода видимой части линии пересечения в невидимую линию всегда находятся на очерковых (контурных) образующих той или другой поверхности.
Пересечение поверхностей вращения
В пересечении двух поверхностей вращения получаются одна или две замкнутые кривые линии. Для решения задач применяют плоскости-посредники, обычно плоскости уровня. На рисунке 6 показано построение линии пересечения полусферы с прямым круговым конусом. Здесь опорными точками будут 1 и 2. Они находятся в пересечении очерковых линий главного меридиана (12) и горизонтальных проекций оснований тел, лежащих в плоскости α4 (22). Нахождение промежуточных точек показано на примере точки 3 при помощи плоскости-посредника α1. Плоскость α1 пересекает заданный конус по окружности радиуса R1 и полусферу по окружности радиусом R 2 . В точках пересечения этих окружностей (на горизонтальной плоскости проекций П 1 ) получаем горизонтальные проекции точки 3 (32 ). Точки А и В, лежащие на образующих профильного меридиана, определяют границу видимых участков линии пересечения А343В3.
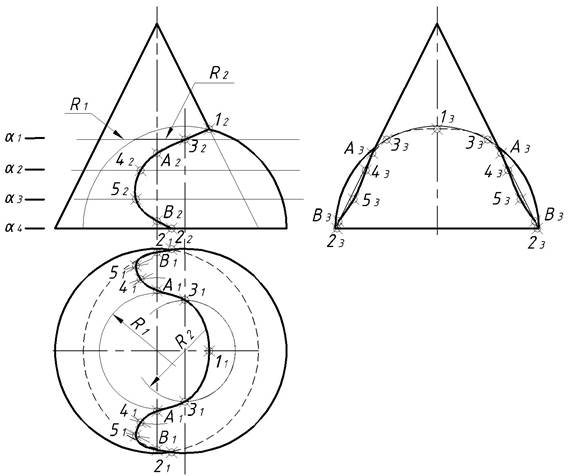
Рисунок 6
Пересечение многогранника с телом вращения
В пересечении тела вращения с многогранником получают одну или две замкнутые линии, отрезки которых являются кривыми или прямыми линиями, которые имеют точки перелома, лежащие на ребрах многогранника. На рисунке 7 изображено пересечение прямого кругового конуса с треугольной призмой, грани которой перпендикулярны плоскости проекции П2. В данном примере применение плоскостей, параллельных горизонтальной плоскости проекций, вполне решает вопрос о нахождении точек для искомой кривой.

Рисунок 7
Приложение 2
Вариант 1, 2


Вариант 3, 4


Вариант 5, 6

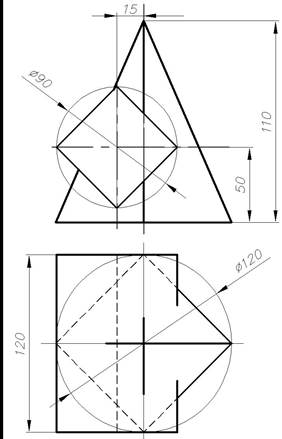
Вариант 7,8

Вариант 9, 10
