Минимизация логических функций

Логическая функция, задающая принцип построения схемы цифрового устройства, может быть, как было пока­зано выше, представлена в виде таблицы истинности или в виде СДНФ или СКНФ и может быть использована для получения логической схемы устройства. Однако получен­ная логическая схема, как правило, не будет оптимальна. Поэтому важным этапом синтеза логических схем являет­ся минимизация логических функций, для чего разрабо­тан ряд методов.

Одним из простых методов минимизации является ме­тод непосредственных преобразований, который осуще­ствляется с использованием основных теорем алгебры логики.

Например, логическую функцию F в виде СДНФ, по­лученную в «Логических функциях и способах их записи», можно минимизировать следующим об­разом:

1. Добавим к данной функции слагаемое х₁•x₂•x₃, ко­торое уже есть в данной функции, используя правило 3 (см. Рис. 4):

 

 

2. Применим метод склеивания (теорема II, рис. 3.26) одинаково подчеркнутых элементарных конъюнкций.

 

 

3.Применим метод склеивания для двух последних элементарных конъюнкций

 

Полученная в результате минимизации логическая функция называется тупиковой. Логическая функция мо­жет иметь несколько тупиковых форм.

Для минимизации логических функций широко ис­пользуется графический метод с помощью карт «Карно» или карт (диаграмм) Вейча, который удобен при неболь­шом числе переменных.

Карты Карно и карты Вейча являются важным сред­ством проектирования логических схем, представляют собой определенную таблицу истинности обычно для двух, трех и четырех переменных и отличаются друг от друга способом обозначения строк и столбцов таблиц ис­тинности. На рис. 5 представлены карты Вейча для двух, трех и четырех переменных соответственно.

 

 

 

 

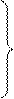
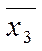
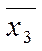
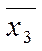
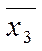
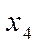
Рис. 5

Расположение групп переменных х, не имеет значения, необходимо лишь, чтобы каждая клетка отличалась от любой соседней лишь на одну переменную. Согласно при­нятой форме построения карт соседними также считают­ся клетки первой и последней строк, клетки первого и последнего столбцов. Число клеток карты равно числу возможных комбинаций значений переменных и в каждую клетку записывается значение логической функции, соот­ветствующее данному набору переменных. Этот набор пе­ременных определяется присвоением значения логичес­кой 1 переменным, на пересечении строк и столбцов которых расположена клетка.

Например, если логическая функция задана таблицей истинности (рис. 6(а)), то карта Карно для нее будет иметь вид, показанный на рис. 6(б).

а) б)

X1	X2	F

 

 

Рис. 6
Булево выражение данной функции имеет вид

 

 

Но для упрощения функции можно использовать и карты Карно, в которых логические 1, записанные в со­седних клетках, обозначают, что соответствующие этим 1 конъюнкции (произведения) отличаются лишь по одной переменной, которые дополняют друг друга и их можно опустить.

Так в первой строке карты Карно (см. рис. 6(б)) пе­ременная х₁ встречается в комбинации с x₂ и, которые дополняют друг друга:

 

 

Таким образом, группируя две соседние клетки в верх­ней строке (контур на рис. 6(б)), можно исключить одну переменную и получить упрошенное выражение - x₁.

Аналогично, группируя две соседние клетки в левом столбце (контур на рис. 6(б)) и исключая отличающие­ся переменные (x₁ и х₁), получим упрощенное выраже­ние — х₂.

Полученные упрощенные выражения объединяют с помощью операции ИЛИ.

Таким образом, упрощенное выражение логической функции будет иметь вид

 

 

Таким образом, соседние клетки карты Карно можно группировать для исключения переменной. Число группи­руемых клеток может быть и больше двух, но их число должно быть четным и они должны соприкасаться (яв­ляться соседними) друг с другом.

Допускается также иметь несколько групп перекрываю­щихся клеток, как в только что рассмотренном примере.

Группироваться могут также клетки первой и послед­ней строк, первого и последнего столбцов, т. е. карту до­пускается сворачивать в цилиндр, как по вертикальной, так и по горизонтальной оси.

Для исключения n переменных общее число группиру­емых клеток должно быть равно 2ⁿ. Так, для исключения одной переменной требуется объединить две соседние клетки, а для исключения трех переменных уже требует­ся объединить восемь соседних клеток.

Таким образом, для того чтобы получить минимизиро­ванную логическую функцию, необходимо сгруппировать все соседние клетки карты Карно, содержащие 1, а затем объединить полученные группы с помощью операции ИЛИ. Клетки, содержащие 1, которые не удалось объеди­нить с другими клетками, образуют в минимизированной логической функции самостоятельные члены, каждый из которых содержит все переменные.

Рассмотрим несколько примеров карт Вейча и спосо­бы построения контуров группировки соседних клеток для получения упрощенной логической функции. Так, карта Вейча для логической функции

 

 

приведена на рис. 7

0

 

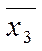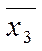Рис. 7

На этом рисунке показан правильный способ объеди­нения соседних ячеек, т. е. карта Вейча как бы свернута в вертикально расположенный цилиндр.

Упрощенное выражение логической функции имеет вид

 

Таким образом, группируя соседние клетки в единый квадрат, удалось исключить две переменные (x₁ и х₂) и получить простое выражение для логической функции.

 

Рис. 8

Рассмотрим пример минимизации логической функции

 

 

для которой карта Вейча имеет вид рис. 8.

Группируемые ячейки обведены двумя контурами. Нижний контур даст возможность исключить одну переменную X₃ и после этого в нем остается член x₁•x₂•x₃. В верхнем контуре можно исключить две переменные(х₂ и x₄) и после этого в нем остается член х₁х₃. Упрошенное булево выражение логической функции имеет вид

 

Можно объединять в квадрат также четыре угловые клетки карты Вейча, как это показано на рис. 9, кото­рая построена для логической функции

 

Рис. 9

 

Объединенные клетки являются соседними (если по­верхность представить в виде тора), и это объединении позволяет исключить две переменные х₁ и x₂ и получить простое выражение логической функции

 

 

Рассмотрим минимизацию логической функции, кар­та Вейча которой представлена на рисунке 10:

 

 

Рис. 10

Булево выражение этой функции имеет вид

 

Четыре угловые клетки можно объединить в одну груп­пу, как это делалось в предыдущем примере. Это объеди­нение позволяет исключить две переменные (х₁ и х₂) и получить член х₃• х₄.

Две единицы из первой строки можно объединить с двумя единицами из нижней строки, получить группу из четырех ячеек, которая позволяет исключить две перемен­ные (х₄ и х₃) и получить член

Наконец, единственную оставшуюся единицу (из вто­рой строки и последнего столбца) можно объединить с клеткой, находящейся над ней, и это позволит исключать одну переменную (x₄) и получить член

Таким образом, мы получим минимизированную логи­ческую функцию

 

Следует отметить, что для получения минимальной формы логической функции необходимо группировать наибольшее число клеток, причем некоторые клетки мо­гут входить в разные группы. В зависимости от выбора групп объединения клеток можно получить несколько упрощенных выражений логической функции,

В ряде случаев не все значения логической функции бывают определены однозначно. Например,в некоторых случаях, известно, что какие-то комбинации входных пе­ременных (сигналов на входе логической схемы) появить­ся не могут, или, если они появляются, то значение логи­ческой функции (сигнала на выходе логической схемы) не существенно. В таких случаях говорят о неопределенных условиях, и на карте Вейча такое неопределенное условие может обозначаться прочерком.

Рассмотрим, как карту Вейча с неопределенными ус­ловиями можно использовать для минимизации логичес­кой функции.

Пусть имеется карта Вейча такой функции (рис. 11)

 

Рис. 11

При минимизации клетки с недоопределенными состо­яниями могут произвольным образом включаться в груп­пы при объединении клеток, причем им может присваи­ваться любое значение (0 или 1) таким образом, чтобы сгруппировать наибольшее число клеток

Так, в рассматриваемом примере вместо всех прочер­ков можно проставить логические 1 и получить две боль­шие группы по восемь клеток (два контура на рис. 11), что позволит исключить три переменные и получить сле­дующее упрошенное выражение логической функции:

 

 

Если клетки с неопределенными условиями не исполь­зовать, то можно получить две группы по четыре клетки, что позволит получить следующее упрощенное выражение логической функции:

 

Очевидно, что данное выражение логической функции сложнее предыдущего.

При минимизации логической функции, содержащей более четырех переменных, используются другие способы минимизации.

Реализация логических функций

Техническая реализация логической функции предпо­лагает построение цифрового устройства, сигналы, на вы­ходе которого определяются сигналами на его входах в соответствии с этой функцией. Для построения цифрового устройства достаточно иметь элементы, реализующие три основные логические операция И, ИЛИ и НЕ. На прак­тике также используют элементы, выполняющие другие простейшие логические операции. Такие элементы назы­вают логическими. Их называют также логическими вен­тилями. Если соединить логические элементы в соответ­ствии со структурой выражения для логической функции, То получим цифровое устройство, реализующее заданную логическую функцию.

Логический элемент может быть реализован в виде интегральной схемы. Часто интегральная схема содержит несколько логических элементов.

На рис. 12 приведены примеры условных графичес­ких обозначений некоторых логических элементов, буле­во выражение реализуемой логической функции и их таб­лицы истинности.

 

 

Рис. 12

 

Положим, что имеется логическая функция вида:

 

По этому выражению можно построить устройство, схема которого приведена на рисунке 13

 

Рис. 13

 

При проектировании цифрового устройства рекомен­дуется поступать следующим образом:

1.По условию работы устройства определяется, что именно должно делать устройство, и уточняется ал­горитм его работы.

2.Составляется таблица истинности для логической функции, реализуемой устройством.

3.Составляется логическая функция и проводится ее минимизация.

4.Разрабатывается схема проектируемого устройства.

Рассмотрим примеры проектирования некоторых циф­ровых устройств.

Пример 1. Необходимо спроектировать устройство включения и выключения звукового сигнала в помещении переключением одного из двух ключей, независимо от состояния другого ключа.

Требуется спроектировать логическое устройство, на выходе которого появляется сигнал логической 1 (F= 1), когда сирена включается. Если ключи (x и у ) замкнуты, то это соответствует логическим нулям на входах устройства (х = 0, у = 0), а разомкнутые ключи соответствуют логи­ческим единицам на входах устройства (x = 1, у = 1).

Учитывая сказанное, составим таблицу истинности (рис. 14).

 

 

Рис. 14

 

Поясним таблицу истинности. При обоих замкнутых ключах сирена включена (первая строка таблицы истинности). Выключение любого из двух ключей приводит к отключению сирены (вторая и третья строки таблицы). Выключение оставшегося включенного ключа приводит к включению сирены (последняя строчка).

По данной таблице истинности составим логическую

функцию

Полученное логическое выражение может быть реали­зовано следующим образом (Рис. 15).

Рис. 15

Пример 2. Требуется спроектировать логическое устрой­ство, осуществляющее передачу данных с одного из четы­рех входов на один выход в зависимости от комбинации сигналов на адресных входах.

Из описания следует; что проектируемое устройство имеет один выход F четыре входа х₁, х₂, х₃, х₄ и на кото­рые могут подаваться логические сигналы 0 или 1, и один из входов должен подключаться к выходу в зависимости от комбинации сигналов на адресных входах. Так как вхо­дов четыре, то, следовательно, и комбинаций на адресных шинах должно быть четыре, а для этого достаточно иметь два адресных входа А₁ и А₂.

С учетом этого описания можно составить следующую таблицу истинности (Рис. 16).

 

 

Рис. 16

Из данной таблицы следует, что при нулях на обоих адресных входах к выходу устройства подключен первый вход данных х₁, при А₁=1, А₂ = 0 к выходу подключен вход данных х₂, при А₁= 0, А₂ = 1 к выходу подключен вход данных х₃,а при А₁= 1, А₂ = 1 к выходу подключен вход данных х₄

По данной таблице составим логическую функцию

 

 

Используя данное выражение, построим логическую схему проектируемого устройства (Рис. 17).

 

Рис. 17

Далее мы увидим, что спроектированное устройство является мультиплексором на четыре входа и находит широкое применение в цифровой электронике.

Особенности построения логических устройств

Обычно при построении логических устройств, с целью сокращения номенклатуры используемых логических эле­ментов, используют либо два элемента, выполняющие операции И-НЕ и ИЛИ-НЕ, либо только один из этих элементов.

Это обусловлено тем, что эти элементы И-НЕ и ИЛИ-НЕ являются универсальными. Универсальность проявля­ется в том, что каждый из них позволяет реализовать все три основные булевы операции И, ИЛИ, НЕ (Рис. 18).

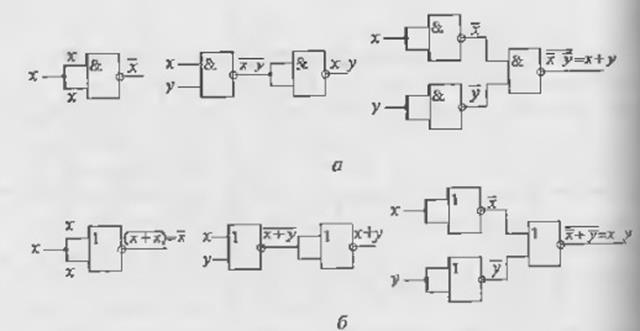
Рис. 18

 

Следовательно, любую логическую функцию можно реализовать, используя только логические элементы И-НЕ или ИЛИ-НЕ.

При построении логического устройства число входов логических элементов обычно бывает задано, что тоже вносит определенные трудности. Для построения устрой­ства на заданных логических элементах И-НЕ или ИЛИ-НЕ необходимо логическую функцию преобразовать к соответствующему виду так, чтобы в ней присутствовали только логические операции И-НЕ или ИЛИ-НЕ. Для этого используют теоремы 5 и 10 (см. рис. 4) булевой алгебры, т. е. двойное отрицание, и теорему Де Моргана. В качестве примера рассмотрим построение логического устройства на двухвходовых элементах И-НЕ и ИЛИ-НЕ по логической функции

 

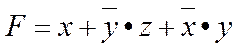
Построим вначале устройство на элементах И-НЕ

 

 

Полученная форма является алгебраической формой

элемента И-НЕ с тремя входами: и , т. е. схема данного устройства будет иметь следующий вид (Рис. 19).

 

Рис. 19

 

Путем несложных преобразований, которые понятны из окончательной схемы устройства (Рис. 20), получим устройство, построенное на двухвходовых элементах И-НЕ с входными сигналами x,y,z.

 

Рис. 20

 

Проводя аналогичные преобразования, функциюFможно реализовать на двухвходовых элементах ИЛИ-НЕ

 

 

Учитывая, что и

,получим:

 

 

Следовательно, схема проектируемого устройства будет иметь следующий вид (Рис. 21).

При реализации цифровых устройств на конкретных логических элементах не все их входы, по ряду причин, могут быть использованы. Обычно с неиспользуемыми входами поступают следующим образом:

 

 

Рис. 21

 

 

- объединяют их с используемыми (с учетом теоремы 3, Рис. 4), если это не ведет к превышению нагру­зочной способности логического элемента, к выхо­ду которого подключены объединенные входы;

- в зависимости от логики работы устройства подают на неиспользуемые входы либо логический 0, либо логическую 1. Для того чтобы не изменять логику работы элемента с неиспользуемыми входами, на них нужно подать: либо логическую 1, если элемент реализует логическую функцию И, так как соглас­но теореме I (см. рис.4)X•1=X либо логичес­кий 0, если элемент реализует логическую функцию ИЛИ, так как согласно теореме I (см. рис. 3.26) х + 0 = х.

Для подачи логического 0 неиспользуемые входы про­сто соединяют с шиной питания («землей»).

Для подачи логической 1 неиспользуемые входы под­ключают к источникам питания микросхем обычно через резисторы (в единицы кОм), предотвращающие пробои неиспользуемых входов.

Реализовать логическую функцию можно не только на основе логических элементов, как это было только что по­казано, но и другими способами, о чем речь пойдет далее.

ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ