Лабораторная работа. Вариант №4.
по дисциплине
« Теория инженерного эксперимента »
специальность «Кораблестроение, океанотехника и системотехника объектов морской инфраструктуры»
Выполнил студент: Конев Г.А.
Группа. КиО – 1.
Руководитель: Голицын В.А.
Санкт – Петербург
2018 г.
Лабораторная работа № 1.
Построение вариационных рядов.
Расчет числовых характеристик.
Цель работы: овладение способами построения рядов распределения и методами расчета числовых характеристик.
Выполнение лабораторной работы № 1 рассмотрим на примере следующей задачи. вариационный полигон эмпирический числовой
Задача. Имеются данные о вводе в эксплуатацию новых газовых скважин за год на различных добывающих районов страны:
Содержание работы: на основе совокупности данных опыта выполнить следующее:
1. Построить ряды распределения (интервальный и дискретный вариационные ряды). Изобразить их графики.
2. Построить график накопительных частот— кумуляту.
3. Составить эмпирическую функцию распределения и изобразить ее графически.
4. Вычислить моду, медиану, выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс.
5. Построить доверительные интервалы для истинного значения измеряемой величины и среднего квадратического отклонения генеральной совокупности.
|
|
6. Раскрыть смысловую сторону каждой характеристики.
Выполнение работы
Обозначим через Х ввод в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны.
1.1. По данным выборки строим интервальный вариационный ряд.
а) Поскольку, как легко выяснить, xmax = 57, xmin = 7, то размах варьирования признака Х равен:
R = xmax –xmin = 57 – 7 = 50.
б) Определяя число k интервалов (число столбцов в таблице) вариационного ряда, положим 
.
в) Длина h каждого частичного интервала равна
Так как исходные данные мало отличаются друг от друга и содержат целые числа, то величину h округляем до целого: 
.
г) Подсчитываем число вариант, попадающих в каждый интервал, по данным выборки. Значение 
, попадающее на границу интервала, относим к левому концу. За начало 
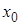первого интервала берем величину
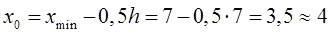
Конец 
последнего интервала находим по формуле
Сформированный интервальный вариационный ряд записываем в виде, записываем в таблицу 1.
Таблица 1. Интервальный вариационный ряд.
| Варианты-интервалы | 4-11 | 11-18 | 18-25 | 25-32 | 32-39 | 39-46 | 46-53 | 53-60 |
| Частоты, ni |
Контроль: 
, и объем выборки 
.
1.2. Записываем дискретный вариационный ряд (табл. 2). В качестве вариант берем середины интервалов интервального вариационного ряда.
Таблица 2. Дискретный вариационный ряд
| варианты, xi | 7,5 | 14,5 | 21,5 | 28,5 | 35,5 | 42,5 | 49,5 | 56,5 |
| частоты, ni |
1.3. Изображаем интервальный и дискретный вариационные ряды графически, построив гистограмму и полигон частот в одной системе координат (рис. 1).
|
|
Рис. 1 Гистограмма и полигон
2. Строим график накопленных частот — кумуляту (рис. 2). Предварительно составляем расчетную табл. 3.
Таблица 3. Накопленные частоты.
Варианты, 
| 7,5 | 14,5 | 21,5 | 28,5 | 35,5 | 42,5 | 49,5 | 56,5 |
| относительные частоты, wi = ni / n | 0,53 | 0,8 | 1,06 | 1,3 | 1,2 | 1,2 | 0,4 | 0,13 |
| Накопительные относительные частоты, Wi = Wi – 1 + wi | 0,53 | 1,3 | 2,4 | 3,73 | 4,26 | 4,8 | 5,2 |
3. Находим эмпирическую функцию распределения. Воспользуемся формулой (1):
Fв (x) 
.
Если х £ 7,5, то Fв (x) = 0 — по свойству эмпирической функции распределения.
Если 7,5< х £ 14,5, то Fв (x) 
.
Если 14,5< х £ 21,5, то Fв (x) 
.
Если 21,5< х £ 28,5, то Fв (x)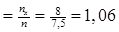 
.
Если 28,5< х £ 35,5, то Fв (x)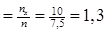 
.
Если 35,5< х £ 42,5, то Fв (x) 
.
Если 42,5< х £ 49,5, то Fв (x) 
.
Если 49,5< х £ 56,5, то Fв (x)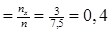 
.
Если х 
56,5, то Fв (x) 
.
Если 
, то Fв (x) = 1 — по свойству эмпирической функции распределения.
Записываем полученную эмпирическую функцию в виде:
Fв (x) 
График функции Fв (x) представлен на рис.3.
Соединив середины вертикальных частей ступенчатой кусочно-постоянной кривой, являющейся графиком функции Fв (x), получаем плавную кривую (на рис. 3 это штриховая линия). Абсциссами точек этой кривой служат значения чисел рабочих дней без простоя для пятидесяти буровых бригад одного из районов страны, а ординатами — значения эмпирической функции распределения, характеризующей оценку вероятности события X £ 
, т.е. вероятности попадания возможных значений чисел ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны на промежуток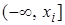 
.
|
|
Для нахождения числовых характеристик признака Х — чисел ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны для пятидесяти буровых бригад (несмещенных оценок для
, 
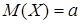а также 
, 
, 
, 
) воспользуемся табл. 2.
4.1. Так как варианта 
в табл. 2 встречается с наибольшей частотой 
, то 
, т.е. это значение ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны, встречающееся в данной выборке с наибольшей частотой.
. Это значение чисел ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны, которое делит данные выборки признака Х на равные части.
Рис. 2 Кумулятивная кривая
4.2. Для нахождения остальных статистик, характеризующих ввод в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны, воспользуемся методом произведений. Введем, согласно, условные варианты:
; 
, 
.
Составим расчетную табл. 4.
Таблица 4. Контрольная
| 
| 
| 
| 
| 
| 
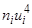
| Контрольный столбец 
|
| 7,5 | -3 | -12 | -108 | ||||
| 14,5 | -2 | -12 | -48 | ||||
| 21,5 | -1 | -8 | -8 | ||||
| 28,5 | |||||||
| 35,5 | +1 | ||||||
| 42,5 | +2 | ||||||
| 49,5 | +3 | ||||||
| 56,5 | +4 | ||||||
Контроль вычислений проводим по формуле:
,
.
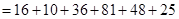Следовательно, вычисления проведены верно.
Рис. 3 Кумулята и эмпирическая функция распределения
4.3. Пользуясь результатами последней строки табл. 4, находим условные начальные моменты:
,
,
,
.
4.4. Находим выборочную среднюю:
,
4.5. Находим выборочную дисперсию:
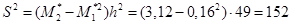
4.6. Вычисляем выборочное среднее квадратичное отклонение:
.
4.7. Величина 
характеризует степень рассеяния значений числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны. Для определения колеблемости значений числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны в процентном отношении вычисляем коэффициент вариации:
.
Величина коэффициента вариации велика (составляет 41%), что означает большой разброс значений числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны.
4.8. Для предварительной оценки отклонения значений числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны от нормального распределения вычисляем асимметрию и эксцесс. Сначала находим центральные моменты третьего и четвертого порядков:
.
.
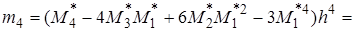
4.9. Тогда, находим:
,
.
Резюме. Значения 
и 
отличаются от нуля. Поэтому можно предположить не близость данной выборки, характеризующей число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны, к нормальному распределению. Эта гипотеза будет проверяться в лабораторной работе № 2.
5. Произведем оценку генеральной средней 
и генерального среднеквадратического отклонения s = S по выборочным статистикам 
и 
, используя теорию доверительных интервалов для нормального распределения. Доверительный интервал для истинного значения числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны с надежностью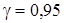 
находим, согласно:
.
Согласно приложению 3, при 
и 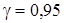находим 
. Записываем доверительный интервал:
,
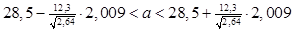или 
.
Таким образом, среднее число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны по данным выборки должна находиться в промежутке 
.
Запишем доверительный интервал для генерального среднеквадратического отклонения 
. При заданных 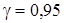и по таблице приложения 4 находим 
. Так как 
, то доверительный интервал записываем в виде:
,
или 
,
или 
;
следовательно, отклонения истинных значений числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны не должны выходить за пределы промежутка 
.
Лабораторная работа№ 2.
Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном рас-определении выборки
Цель работы: овладение студентом способами построения эмпирической и теоретической (нормальной) кривой распределения; выработка умения и навыков применения критериев согласия для проверки выдвинутой статистической гипотезы.
Содержание работы: на основе дискретного вариационного ряда, полученного в лабораторной работе № 1, выполнить следующее:
1. Построить эмпирическую (полигон) и теоретическую (нормальную) кривую распределения.
2. Проверить согласованность эмпирического распределения с теоретическим нормальным, применяя три критерия:
а) критерий Пирсона; б) один из критериев: Колмогорова, Романовского; в) приближенный критерий.
Выполнение работы
Рис 4. Эмпирическая и теоретическая кривые.
Продолжим вероятностно-статистическую обработку результатов эксперимента, предложенных в лабораторной работе № 1, то есть число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны. За основу берем дискретный вариационный ряд в табл. 2.
Таблица 5. Дискретный вариационный ряд
| варианты, xi | 7,5 | 14,5 | 21,5 | 28,5 | 35,5 | 42,5 | 49,5 | 56,5 |
| частоты, ni |
и значения 
и S = 12,3. Эмпирическая кривая распределения представляет собой полигон частот (см. лабораторную работу № 1). Для построения теоретической (нормальной) кривой найдем координаты точек (xi, n¢i), для чего рассчитаем теоретические частоты n¢i (табл. 6).
Таблица 6. Теоретические частоты.
| xi | ni | xi - 
| 
| j(ui) | уi = nh j(ui) S | n¢i |
| 7,5 | –21 | –1,707 | 0,0833 | 2,37 | ||
| 14,5 | –14 | –1,138 | 0,1989 | 5,65 | ||
| 21,5 | –7 | –0,569 | 0,3352 | 9,55 | ||
| 28,5 | 0,3989 | 11,35 | ||||
| 35,5 | 0,569 | 0,3352 | 9,55 | |||
| 42,5 | 1,138 | 0,1989 | 5,65 | |||
| 49,5 | 1,707 | 0,0833 | 2,37 | |||
| 56,5 | 2,276 | 0,0310 | 0,88 |
Строим эмпирическую и теоретическую кривые (рис. 4).
Проверим согласованность эмпирического распределения (число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны) с теоретическим нормальным по критерию Пирсона.
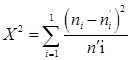
Для нахождения суммы составляем расчетную таблица 7.
Таблица 7. Расчетная таблица суммы по критерию Пирсона.
| ni | 
| ni -
| (ni - )2
| (ni - ni ¢)2
ni ¢
|
| –1 | 0,25 | |||
| 0,125 | ||||
| 6,4 | ||||
| 44,4 | ||||
| 0,444 | ||||
| –1 | 0,333 | |||
| c2 = 132,952 |
Находим число степеней свободы k = s - r = s - 3 = 8 - 3 = 5.
Выбираем уровень значимости, a = 0,95. По таблице критических точек распределения c2 (приложение 5) находим c2кр=2,17. Так как c2кр < c20, (1,15<132,952) то делаем вывод, что данные выборки, характеризующие число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны, не подчиняются нормальному закону распределения.
Проведём проверку близости эмпирического распределения к нормальному по критерию Романовского.
Расхождение между эмпирическим и теоретическим распределением несущественно, что позволяет утверждать, что данные выборки, характеризующие число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны по критерию Романовского, подчиняются нормальному закону распределения.
Критерий Колмогорова в своем классическом виде является более мощным, чем критерий Пирсона, и может быть использован для проверки гипотезы о соответствии эмпирического распределения любому теоретическому непрерывному распределению F(x) с заранее известными параметрами. Однако параметры функции распределения F(x), как правило, нам неизвестны, и их оценка производится по данным самой выборки. Это обстоятельство накладывает ограничения на возможность широкого практического применения критерия: он может быть использован только для проверки соответствия опытных данных лишь некоторым конкретным функциям распределения. Для проверки соответствия экспоненциального распределения нормальному распределению критерий Колмогорова применяют следующим образом.
Неравенство при выбранном 
не выполняется, это означает, что эмпирическое распределение нельзя изучать на математической модели, подчиняющейся экспоненциальному закону распределения.
Наконец, проведём проверку близости рассматриваемой выборки к нормальному распределению по приближенному критерию, используя выборочные статистики: асимметрию, эксцесс и их средние квадратические отклонения. В лабораторной работе № 1 были найдены As=0,053 и Ex=-0,864.
Найдем средние квадратические отклонения для асимметрии и эксцесса:
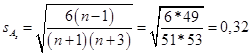
Так-как |As| = 0,053 < SAs и |Ex| = -0,864 < SEx, то делаем вывод, что данные выборки, характеризующие число ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны, не подчиняются нормальному закону распределения.
Итак, для проверки согласованности эмпирического распределения с теоретическим нормальным мы применили 4 критерия, один из них подтвердил близость выборочной совокупности к нормальному распределению, три не подтвердили. Исходя из этого заключаем, что за закон распределения признака Х — для числа ввода в эксплуатацию новых газовых скважин за год из рассматриваемых различных добывающих районов страны — нельзя принять нормальное распределение.