2. Гнеденко Б.В. Курс теории вероятностей. – М.: Нука, 1988.
3. Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1982.
4. Зубков А.М., Севастьянов Б.А., Чистяков В.П. Сборник задач по теории вероятностей. – М.: Наука, 1989.
5. Колемаев В.А., Староверов О.В., Турудаевский В.Б. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1991.
6. Сборник задач по математике для ВТУЗов. Ч. 3. Теория вероятностей и математическая статистика/Под. Ред. Ефимова А.В. – М.: Наука, 1990.
7. Феллер В. Введение в теорию вероятностей и её приложения. Т. 1, 2. – М.: Мир, 1984.
8. Ширяев А.Н. Вероятность. – М.: Наука, 1980.
Справочники
1. Справочник по математике для экономистов /Под ред. В.И. Ермакова. М.: Высшая школа, 1987.
Правила выбора варианта контрольной работы, ее оформление и зачета
1. Впроцессе изучения высшей математики студент первого курса должен выполнить две контрольные работы, задачи второй из которых содержатся в разделе «Варианты контрольной работы». Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
2. Контрольные работы должны быть оформлены в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
3. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
4. На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, факультет (институт), номер группы, название дисциплины (высшая математика), номер контрольной работы, номер варианта и домашний адрес студента. В конце работы следует поставить дату ее выполнения и расписаться.
5. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.
6. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.
При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса.
Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа я, е и т. д.
Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Так, например, вычислив неопределенный интеграл, нужно проверить, равна ли подынтегральная функция производной от полученной первообразной. Полезно также, если это возможно, решить задачу несколькими способами и сравнить полученные результаты.
8. Срок проверки контрольных работ - 10 рабочих дней. Студенты обязаны сдавать письменные контрольные работы не позднее, чем за 10 дней до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.
9. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и прислать работу для повторной проверки. В связи с этим рекомендуем при выполнении контрольной работы оставить в конце тетради несколько чистых листов для внесения исправлений и дополнений впоследствии.
В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При представленных на повторную проверку исправлениях обязательно должны находиться прорецензированная работа и рецензия на нее. Вносить исправления в сам текст работы после ее рецензирования запрещается.
10. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. На экзамен студент должен явиться с рецензией на выполненную контрольную работу. Без предъявления преподавателю прорецензированных контрольных работ студент к экзамену не допускается
ВАРИАНТЫКОНТРОЛЬНОЙ РАБОТЫ
Далее приведены варианты контрольной работы. Отметим, что номер варианта контрольной работы, выполняемой студентом, должен совпадать с последней цифрой номера его зачетной книжки.
Вариант О.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1,D1. Найдите:
а) длину ребра 
;
б) косинус угла между векторами и 
;
в) уравнение ребра ;
г) уравнение грани С1;
если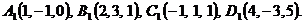 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
3. Имеются 12 единиц товара в одинаковых упаковках. Известно, что в четырех из них товар первого сорта. Случайным образом отбирают 3 единицы товара. Вычислить вероятность того, что среди них:
а) только упаковки с товаром первого сорта;
б) ровно одна упаковка с товаром первого сорта.
4. В магазин поступила обувь от двух поставщиков. Количество обуви, поступившей от первого поставщика, в 2 раза больше, чем от второго. Известно, что в среднем 20% обуви от первого поставщика и 35% обуви от второго поставщика имеют' различные дефекты отделки. Из общей массы наугад отбирают одну упаковку с обувью. Оказалось, что она не имеет дефекта отделки. Какова вероятность, что её изготовил первый поставщик?
5. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | |||||
| Р | 0,01 | Р | 0,23 | 0,28 | 0,19 | 0,11 | 0,06 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения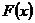 
и построить её график;
г) закон распределения случайной величины 
, если её значения заданы функциональной зависимостью 
6. Известно, что в среднем 64% студентов потока выполняют контрольные работы в срок. Какова вероятность того, что из 100 студентов потока задержат представление контрольных работ:
а) 30 студентов; б) от 30 до 40 студентов?
Вариант 1.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
3. В коробке 25 одинаковых по форме шоколадных конфет. Известно, что 15 штук из них сорта «Мишка на Севере», а остальные — сорта «Красная Шапочка». Случайным образом выбирают 3 конфеты. Вычислите вероятность того, что среди них: а). Все конфеты сорта «Мишка на Севере»; б). Только одна конфета этого сорта.
4. В магазин поступил одноименный товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц первого сорта, а со второго предприятия 200 единиц, из них 50 первого сорта. Из общей массы товара наугад извлекается одна единица товара 1-го сорта. Какова. вероятность того, что она изготовлена на первом предприятии?
5. Задан закон распределения дискретной случайной величины X:
| X | -2 | -1 | |||||
| P | 0,2 | 0,31 | 0,24 | p | 0,07 | 0,04 | 0,01 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение <т данной случайной величины;
в) функцию распределения 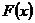и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
6. Известно, что в среднем 14% стаканов, изготовляемых на данном предприятии, имеет дефект. Какова вероятность того, что из 300 стаканов данной партии:
а) имеют дефект 45;
б) не имеют дефекта от 230 до 250?
Вариант 2.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера,
б) методом Гаусса:
3. В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислите вероятность того, что из членов группы в первом отеле: а) все туристы говорят хорошо по-английски;
б). Только один турист хорошо говорит по английски.
4. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый из двух магазинов зависят от их местоположения и соответственно равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 для второго. Какова вероятность того, что покупатель приобретет нужный ему товар.
5. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | |||||
| Р | 0,04 | 0,08 | 0,3 | 0,3 | 0,1 | 0,08 | Р |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения 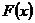и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью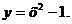 
6. Установлено, что предприятие бытового обслуживания выполняет в срок в среднем 60% заказов. Какова вероятность того, что из 150 заказов, принятых в течение некоторого времени, будут выполнены в срок:
а) 90 заказов; б) от 93 до 107 заказов?
Вариант 3.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
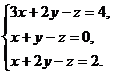
3. В упаковке 12 одинаковых книг. Известно, что каждая третья книга имеет дефект обложки. Случайным образом выбирают 3 книги. Вычислите вероятность того, что среди них: а) все книги имеют дефект обложки; б). Только одна книга имеет этот дефект.
4. Два контролера производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет к первому контролеру, равна 0,55; ко второму контролеру — 0,45
Первый контролёр выявляет дефект с вероятностью 0,8, а второй - с вероятностью 0,9. Вычислите вероятность того, что изделие с дефектом будет признано годным к эксплуатации.
5. Задан закон распределения дискретной случайной величины X эксплуатации.
| X | -2 | -1 | |||||
| р | 0,42 | 0,23 | р | 0,10 | 0,06 | 0,03 | 0,01 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения 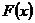и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью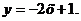 
6. Известно, что в данном технологическом процессе 10% изделий имеют дефект. Какова вероятность того, что в партии из 400 изделий:
а) не будут иметь дефекта342 изделия;
б) будут иметь дефект от 30 до 52 изделий.
Вариант 4.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
3. К экзамену приготовлено 24 одинаковых ручек.. Известно, что треть из них имеет фиолетовый стержень, остальные - синий стержень. Случайным образом отбирают три ручки. Вычислить
вероятность того, что;
а) все ручки имеют фиолетовый стержень; б) только одна ручка имеет фиолетовый стержень.
4. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую - 0,6. Вероятность того, что к моменту прихода пассажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?
5. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | |||||
| Р | Р | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения 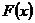и построить её график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью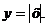 
6. По данным телеателье установлено, что в среднем 20% цветных телевизоров выходят из строя в течение гарантийного срока. Какова вероятность того, что из 225 проданных телевизоров будут работать исправно в течение гарантийного срока:
а) 164 телевизора;
б) от 172 до 184 телевизоров.
Вариант 5.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
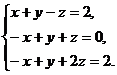
3. В нижней палате парламента 40 депутатов, среди которых первая партия имеет 20 представителей, вторая — 12 представителей, третья 5 представителей, а остальные считают себя независимыми. Случайным образом выбирают трех депутатов. Вычислите вероятность того, что среди них:
а). Только представители первой партии, б). Только один депутат из первой партии.
4. Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым 0,9. Из массы проверенных изделий наугад выбрано одно, оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?
5. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | |||||
| Р | 0,05 | 0,12 | 0,18 | 0,30 | Р | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднееквадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
6. При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин:
а) будут иметь дефекты отделки 60 пар;
б) не будут иметь дефектов отделки от 120 до 148 пар.
Вариант 6.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
3. В ящике 18 одинаковых бутылок пива без этикеток. Известно, что треть из них «Жигулевское». Случайным образом выбирают 3 бутылки. Вычислите вероятность того, что среди них: а) только пиво сорта «Жигулевское»; б) ровно одна бутылка этого сорта.
4. В двух одинаковых коробках находятся карандаши "Конструктор". Известно, что треть карандашей в первой коробке и 0,25 во второй имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен из первой коробки?
5. Задан закон распределения дискретной случайной величины X:
| х | -2 | -1 -1 | |||||
| р | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | Р | 0,03 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
6. Известно, что вероятность рождения мальчика равна 0,51, а девочки 0,49. Какова вероятность того, что 300 новорожденных окажется:
а) 150 мальчиков;
б) от 150 до 200 мальчиков?
Вариант 7.
1. В декартовой прямоугольной системе координат даны вершины пирамиды А1, B1, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если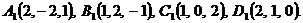 
2. Решите системулинейных уравнений
а) методом Крамера;
б) методом Гаусса;
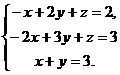
3. В студенческой группе 20 девушек. Известно, что 5 из них не любят читать детективы. Случайным образом выбирают трех девушек и дарят им по детективу. Вычислите вероятность того, что: а). Все девушки оценят этот подарок; б). Только одна девушка оценит этот подарок.
4. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно, что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?
5. Задан закон распределения дискретной случайной величины X:
| х | -2 | -1 -1 | |||||
| р | 0,06 | р | 0,12 | 0,2 | 0,3 | 0,1 | 0,03 |
Найти;
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D к среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью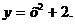 
6. Вероятность нормального расхода электроэнергии за день ша предприятии бытового обслуживания равна 0,7. Какова вероятность того, что из 90 дней предприятие нормально расходует электроэнергию:
а) в течение 60 дней;
б) от 60 до 90 дней?
Вариант 8.
1. В декартовой прямоугольной системе координат даны вершины пирамиды 
, C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
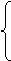3x+z = - 1
5х + 2у + Зz = 3,
7x + 3 у + 5z =6.
3. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а). Все монеты имеют нестандартный процент содержания золота; б). Только одна монета имеет нестандартный процент содержания золота.
4. Магазин получил две равные по количеству партии одноименного товара. Известночто, 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
5. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | |||||
| Р | 0,02 | 0,38 | 0,30 | р | 0,08 | 0,04 | 0,02 |
Найти:
а) неизвестную вероятность р;
6) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины.
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью 
6. Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию:
а) 50 раз;
б) от100 до 150 раз?
Вариант 9.
1. В декартовой прямоугольной системе координат даны вершины пирамиды , C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если 
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
3. На витрине 32 одинаковых булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что: а). Все выбранные булочки с изюмом; б). Только одна булочка с изюмом.
4. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?
5. Задан закон распределения дискретной случайной величины X:
| Х | -2 | -1 | |||||
| р | 0,08 | 0,1 | 0,14 | 0,1 | 0,1 | 0,1 | р |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить ей график;
г) закон распределения случайной величины , если её значения заданы функциональной зависимостью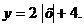 
6. Установлено, что третья часть покупателей, при посещении модного магазина приобретает себе одежду. Какова вероятность того, что из 150 посетителей магазина:
а) ровно 50 человек приобретут товар;
б) от 100 до 120 человек приобретут товар?
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ КВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Векторная алгебра иэлементы аналитической геометрии
Для решениязадачи 1и задачи2 необходимо изучить следующую литературу:
Глава 3, стр.63-74,
Глава 4, стр. 95-101
Глава 9. § 1-13. стр. 222-251
Теперь рассмотрим применение изученныхформул напримерах.
ЗАДАЧА 1.
В декартовой прямоугольной системе координат даны вершины пирамиды 
.
Найдите:
а) длину ребра ;
б) косинус угла между векторами 
и 
;
в)уравнение ребра ;
г) уравнение грани С1;
если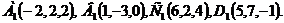 
Решение.
а) Найдем координаты вектора А1В1 по формуле
где 
- координаты точки А1, 
-координаты точки В1.
Итак ={1-(-2);-3-2;0-2}={3;-5;-2}. Тогда 
= 
= 
.
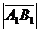Итак, длина отрезка, 
(или длина вектора ) равна . Это иесть искомая длинаребра.
б) Координаты ={3;-5;-2} уже известны, осталось определить координаты вектора 
={6- (-2); 2 - 2; 4 - 2}= {8,0; 2}.
Угол между векторами и вычислим по формуле
cos φ = 
где скалярное произведение векторов А1В1 и А1С1 равно (, )=3·8+(-5)·0+(-2)=24+0-4=20,
| |= , | |= 
= 
.
Итак, cos φ = 20 = 10
· 
в)Координатыточки А1(-2,2,2) обозначим соответственно Х0 = -2, У0 = 2, Z0 = 2, а координаты точки В1(1,-3,0) через X1 = 1, У1 = -3, Z1 = 0 и воспользуемся уравнением прямой и пространстве, проходящей через две точки:
.
Следовательно, уравнение ребра имеет вид
.
г) Обозначим координаты векторов , и черезХ1=3, У1= -5, Z 1= -2 и Х2=8, У2 = 0, Z2=2 соответственно. Векторное произведениеданныхвекторов определяется формулой
·A1C1 = {Y1·Z2-Y2·Z1;Z1·X2-Z2·X1;X1·Y2-X2·Y2} =
= {(-5)·2-0·(-2);-2·8-2·3;3·0-8·(-5)}={-10,-22,40}
Так как данный векторперпендикуляренграни С1,то можно воспользоватьсяуравнением плоскости, проходящейчерез точку (Х0 У0, Z0) перпендикулярно вектору{А;В; С}, котороеимеет вид A·(X-X0)+B·(Y-Y0)+С·(Z-Z0)=0.
Подставим координаты точки А1 (Хо= -2, У0=2, Z0=2) и координаты перпендикулярного вектора А= -10, В= -22, С=40 в это уравнение:
- 10 (X + 2) - 22 (У – 2) т 40 (Z- 2) - 0. Раскроем скобки и приведем подобные члены - 10 х -22 у + 40z + (-20 + 44-80)=0. Итак, уравнение грани ,C1 имеет вид: -10х- 22у + 4О z-56=0 или -5х- lly + 20z-28=0.
ЗАДАЧА 2.
Решите систему линейных уравнений
а)методом Крамера;
б) методом Гаусса;
Решение.
а) Решим данную систему уравнений с помощью формул Крамера (см.[2] глава 10. стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
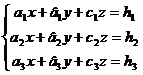
Решение.
а) Решим данную систему уравнений с помощью формул Крамера (см. [2] глава 10, стр. 268).
Тогда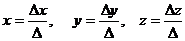 
, где
Так как Δ x = -60; Δ y = -60; Δ