ГРАЖДАНСКОЙ АВИАЦИИ»
КУРСОВАЯ РАБОТА НА ТЕМУ
Исследование детерминированных периодических сигналов и процесса их прохождения через линейные цепи
Работу выполнил:
ОрТОП 0914.0269
(факультет, направление, уч. группа, шифр)
Макарова А.К.
(фамилия, и. о. студента)
Работу проверил:
Кудряков С.А.
(фамилия, и. о. преподавателя)
Оглавление
Введение. 5
Часть 1. Разложение периодического сигнала в ряд Фурье. 6
1.1 Аналитический метод нахождения коэффициентов ряда Фурье. 7
1.2 Численный способ определения коэффициентов ряда Фурье. 9
1.3 Имитационное моделирование аппроксимации исходного сигнала рядом Фурье. 12
Часть 2. Исследование временных и частотных характеристик линейной цепи с постоянными параметрами. 13
2.1 Определение передаточной функции и частотной передаточной функции (комплексного коэффициента передачи) для заданной линейной цепи. 13
2.2 Определение временных и частотных характеристик исследуемой линейной цепи. 14
2.3 Определение частотных характеристик исследуемой линейной цепи путем имитационного моделирования. 15
Часть 3. Прохождение периодического сигнала через линейные цепи. 18
Часть 1. Разложение периодического сигнала в ряд Фурье.
Исходный сигнал представлен на рисунке 1.1.
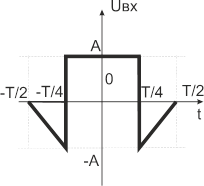
Рисунок 1.1. Исходный сигнал
Аналитическое представление функции, изображенной на рисунке 1, представлено ниже:
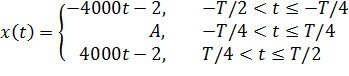
Для данного сигнала заданы:Т=0.001 с и A=1 B.
Найдем коэффициенты ряда Фурье для заданного сигнала следующими методами: аналитический, численный, а также методом имитационного моделирования по средствам программного обеспечения Multisimпро аппроксимируем заданный сигнал.
Аналитический метод нахождения коэффициентов ряда Фурье.
Для вычисления коэффициентов ряда Фурье воспользуемся уравнениями следующего вида:
|
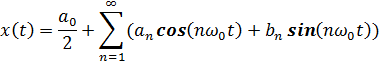
или
|
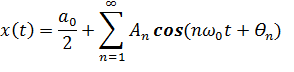
Коэффициенты ряда Фурье найдем по следующим формулам:
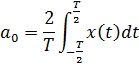
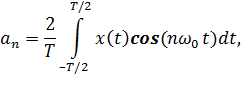
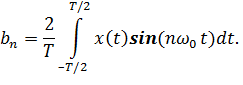
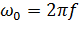
Найдем коэффициенты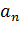 
:
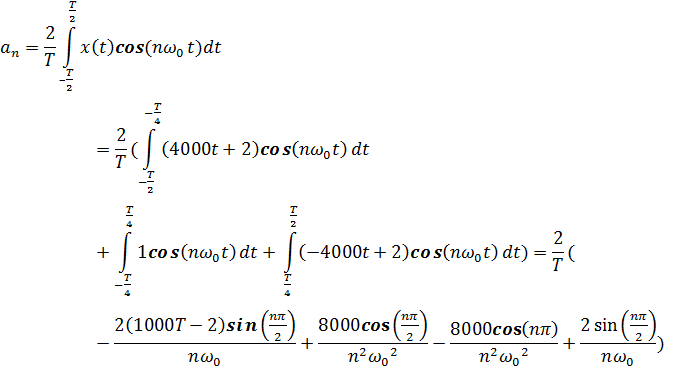
Для подтверждения правильности нахождения общего решения 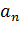, найдем 
:
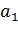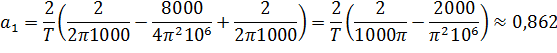
Найдем значение постоянной составляющей 
:
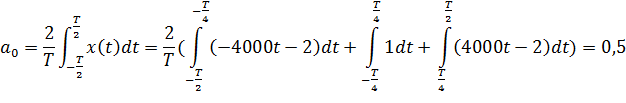
Численный способ определения коэффициентов ряда Фурье
Для численного решения поставленной задачи воспользуемся компьютерной программой Mathcad. Результаты моделирования представлены на рисунке 1.2.
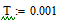Период исследуемой функции
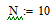Максимальное число учитываемых членов рядя Фурье
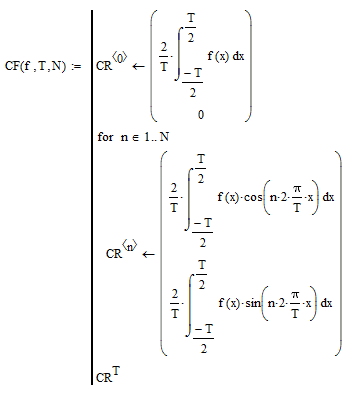
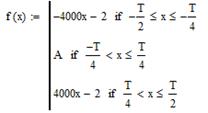Формирование одного периода исследуемого сигнала
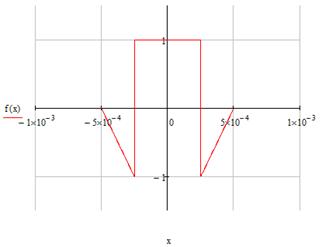График одного периода исследуемого сигнала
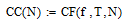
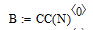
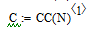
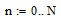
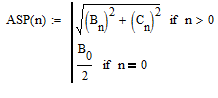
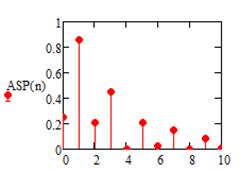Амплитудный спектр анализируемого сигнала
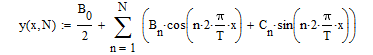Задание аппроксимирующей функции
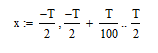Задание интервала для численного моделирования
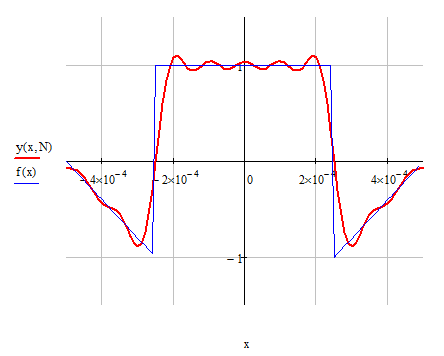График исходного сигнала и его аппроксимации
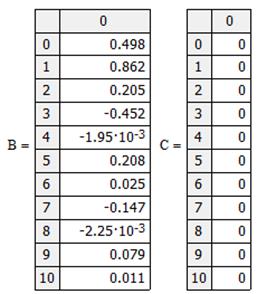Коэффициенты ряда Фурье
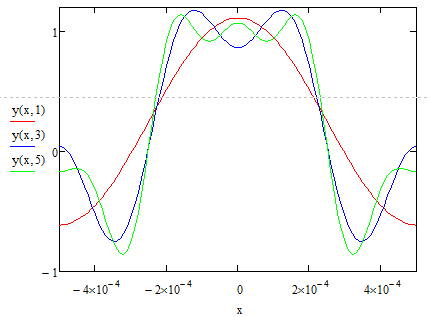Вид аппроксимирующих функций для n=1,3,5
|
| Рисунок 1.2. Численный расчет коэффициентов ряда Фурье |
Имитационное моделирование аппроксимации исходного сигнала рядом Фурье.
Воспользуемся результатами по вычислению коэффициентов ряда Фурье для заданного сигнала, полученными в разделах 1.1 и 1.2.
Произведем восстановление исходного сигнала по первым трем гармоникам. Для моделирования каждой гармоники воспользуемся источниками переменного напряжения соответствующих частот.
Соотношения амплитуд выбранных источников переменного напряжения сохраним в соответствии с полученными ранее уравнениями для коэффициентов ряда Фурье
Результат имитационного моделирования по первым пяти гармоникам представлен на рисунке 1.3.
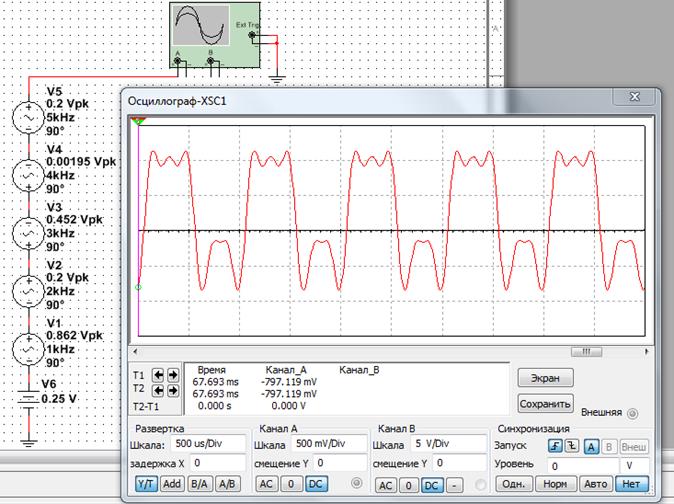
Рисунок 1.3. Восстановление исходного сигнала по первым пяти гармоникам