Маршрутный лист для учащегося
| Предмет
| Геометрия
| | Ф.И.О. учителя
| Куклина М.Б.
| | Тема урока:
| Равнобедренный треугольник.
| | Цели обучения (кратко)
| 1. Познакомить учащихся со свойствами равнобедренного треугольника; применять свойства равностороннего треугольника при решении задач.
| | Порядок действий
| Ресурсы (заполняется учителем)
| Выполнение (заполняется учеником)
| | Ответь
Изучи
Для тех, у кого не откроется видеоурок!
| Добрый день, ребята.
Открываем рабочую тетрадь
Записываем тему урока и число.
1. На каких рисунках изображены: медианы:
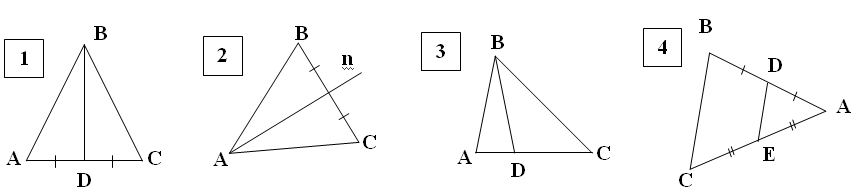2. На каких рисунках изображены: биссектрисы
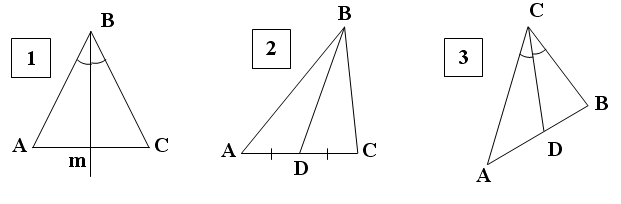3. На каких рисунках изображены: высоты
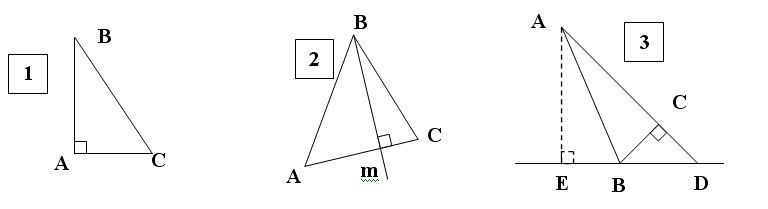Изучение нового материала.
1. Просмотри видеоурок по ссылке:
https://www.youtube.com/watch?v=5spmCxCieVg
2. Прочти материал учебника стр. 34, параграф 18 ( Для тех, у кого не откроется видеоурок!)
Запиши формулировку определений и выполни соответствующие чертежи в тетрадь для теорем.
Вопрос: дать определение равнобедренного треугольника?
Треугольник, у которого все стороны равны, называется равносторонним.
Практическое задание:
1. Построить равнобедренный треугольник ABC (BC – основание)
2. Провести биссектрису AD (с помощью транспортира).
     
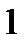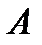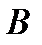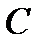Вопрос: какие еще равные элементы вы замечаете в этом треугольнике?
теорема:
В равнобедренном треугольнике углы при основании равны
(первое свойство равнобедренного треугольника).
Обратная теорема: если в треугольнике 2 угла равны, то он равнобедренный
(изменить порядок вершин)
Вопросы учителя: - Какие треугольники мы видим на рисунке?
- Какие равные элементы можно выделить в этих треугольниках?
- Что можно сказать об элементах равных треугольников?
В доказательстве этой теоремы скрыто еще одно свойство равнобедренного треугольника: мы доказали равенство треугольников ABD и ACD, но не назвали соответствующие равные элементы. Какие же элементы остались неназванными?
BD = DC и ﮮADB = ﮮ ADC.
Делаем вывод: AD – медиана и высота.
Теорема:
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
Обрати внимание биссектриса проводится к основанию, две другие биссектрисы таким свойством не обладают.
| Отметь знаком «+» материал, с которым ознакомился(лась)
| | Выполни
В тетради!
Соблюдай правила оформления задачи!
| Реши задачу:
• В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите периметр треугольника.
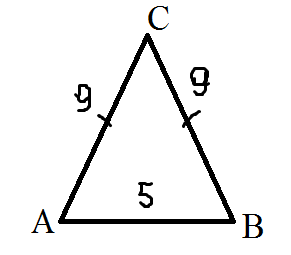Дано: ∆АВС, АС=ВС=9см, АВ=5см
Найти:Р∆
Решение:
По определению равнобедренного треугольника на чертеже сразу отметим все известные величины, и сделаем вывод что АС=СВ
Р=АС+СВ+АВ= 9+9+5=23см.
Ответ: 23 см.
САМОСТОЯТЕЛЬНО
• В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.
Используя пройденные свойства реши задачи на готовых чертежах
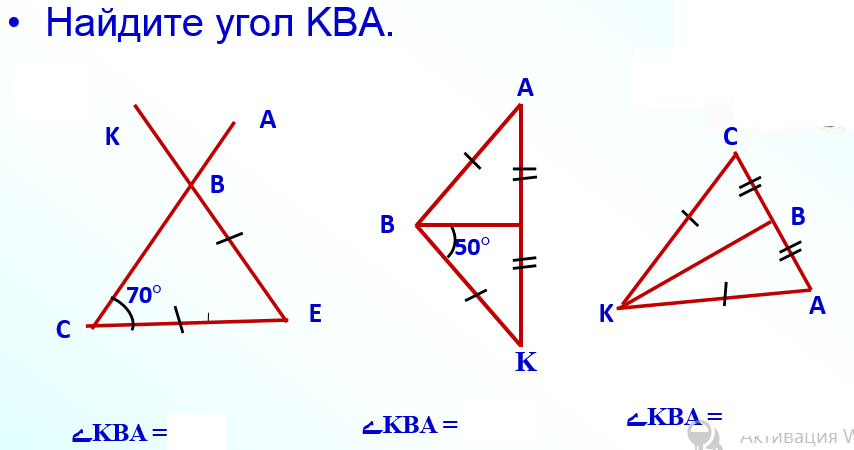По первому чертежу
Решение:
Треугольник равнобедренный видим по чертежу ЕС=ЕВ. По теореме о углах при основании следует <С= <В, <КВА и <В треугольника- вертикальные. Вертикальные углы равны. Следует <КВА=700
САМОСТОЯТЕЛЬНО остальные задачи.
домашняя работа на неделю с 13.11 по 27.11: (жирным шрифтом задачи на сегодня! Два других к следующему уроку-тема еще не пройдена)
№109, №119,№124,№125.
|
| | Рефлексия
| Было легко работать с заданиями
Затруднения возникли в заданиях с номерами…
| О затруднениях напиши в беседу
| | | | | |
|
Поиск по сайту:
|