СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
Статически неопределимыми называют системы, для определения усилий во всех элементах которых, уравнений равновесия (условий статики) недостаточно. Дополнительными являются условия совместности перемещений. Дополнительных уравнений должно быть составлено столько сколько не хватает уравнений равновесия. В этих дополнительных условиях перемещения выражают через усилия по закону Гука. Поэтому число неизвестных становится равным общему числу уравнений и система уравнений превращается в разрешимую.
При расчёте статически неопределимой системы методом сил используется так называемая основная (по её роли в расчёте) система. Она получается отбрасыванием из заданной системы связей как бы лишних с точки зрения геометрической неизменяемости. В этой основной системе вычисляют перемещения по направлению отброшенных связей отдельно от внешних нагрузок и от неизвестных усилий, заменивших отброшенные связи. Затем сумму перемещений по направлению каждого неизвестного приравнивают нулю, так как в заданной системе здесь находилась связь. Этим обеспечивается эквивалентность основной системы заданной. Число уравнений совместности перемещений становится равным числу усилий в отброшенных связях и система уравнений превращается в разрешимую и без уравнений равновесия.
Раскрытие статической неопределимости систем методом сил

 Общий порядок расчета рассмотрим на примере плоской рамы, изображенной на рис.3.1. Система представляет собой сплошной диск без промежуточных шарниров и замкнутых контуров и имеет шесть внешних связей, значит она трижды статически неопределима. Система канонических уравнений имеет вид
Общий порядок расчета рассмотрим на примере плоской рамы, изображенной на рис.3.1. Система представляет собой сплошной диск без промежуточных шарниров и замкнутых контуров и имеет шесть внешних связей, значит она трижды статически неопределима. Система канонических уравнений имеет вид

Выберем основную систему такую
,рис.3.2, чтобы как можно проще
выглядела грузовая эпюра М р.
Грузовая и единичные эпюры
изгибающих моментов показаны
на рис.3.3
Для построения грузовой эпюры
|



Значение момента в узле В
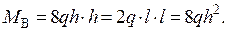
|
|
|
|
|
лим опорную реакцию R а

|
Значение момента в узле В 
Еще проще построение эпюр  .
.
 | |||
|
Коэффициенты системы уравнений δik и ∆ i p определим перемножая эпюры. В нашем случае все коэффициенты будут не равны нулю и нужно решать систему из трех уравнений с тремя неизвестными.
 Но данную задачу можно решить проще. Дело в том, что внутренние усилия в свободной консоли 1-3 не зависят от усилий в остальной раме. Силы, действующие на консоль перенесем в узел 1 (рис.3.4).
Но данную задачу можно решить проще. Дело в том, что внутренние усилия в свободной консоли 1-3 не зависят от усилий в остальной раме. Силы, действующие на консоль перенесем в узел 1 (рис.3.4).
|
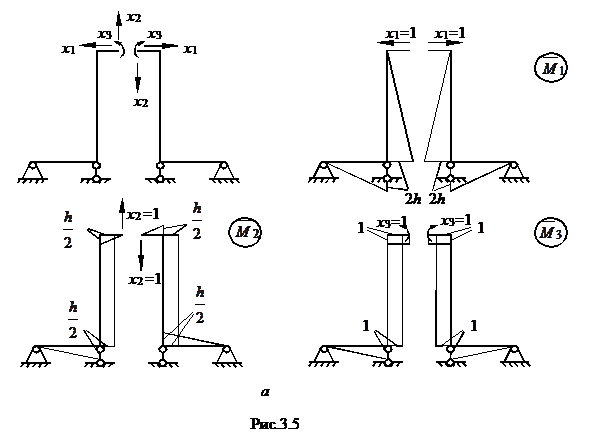 Рама превратилась в симметричную и ее можно рассчитать с учетом симметрии. Основная система и единичные эпюры показаны на рис.3.5. Грузовая эпюра останется, как на рис. 3.3
Рама превратилась в симметричную и ее можно рассчитать с учетом симметрии. Основная система и единичные эпюры показаны на рис.3.5. Грузовая эпюра останется, как на рис. 3.3
 Вычислим коэффициенты при неизвестных системы уравнений, перемножая единичные эпюры по правилу Верещагина:
Вычислим коэффициенты при неизвестных системы уравнений, перемножая единичные эпюры по правилу Верещагина:
|
|
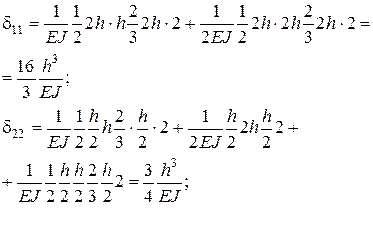
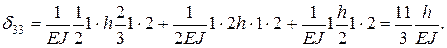
δ12=δ23=0, так как эпюра М2 кососимметричная,а М1 и М3 симметричны.

Для проверки правильности этих вычислений построим суммарную единичную эпюру (рис.3.6). Например, на участке С-2
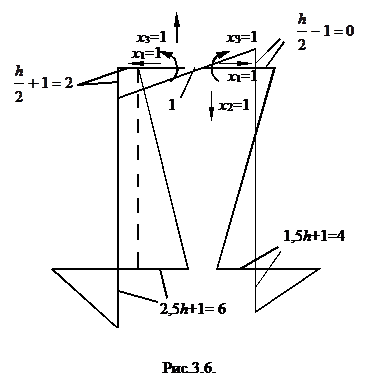 |

Так как вычисления в общем виде уже затруднительны, примем h = 2 м.
Перемножим суммарную единичную эпюру саму на себя
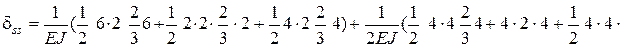
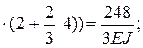
|
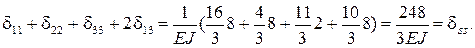
 Коэффициенты при неизвестных вычислены. Для вычисления свободных членов эпюру Мр на участке В1 (рис.3.3) разобьем на простейшие фигуры (рис.3.7): пря
Коэффициенты при неизвестных вычислены. Для вычисления свободных членов эпюру Мр на участке В1 (рис.3.3) разобьем на простейшие фигуры (рис.3.7): пря
|



Принимаем q = 10 кН/м, тогда

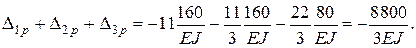
Перемножаем грузовую эпюру на суммарную единичную.

Свободные члены системы уравнений вычислены верно.
Вычисленные значения коэффициентов подставляем в исходную систему уравнений

система уравнений распалась 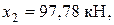 нужно решать всего два уравнения с двумя неизвестными (отметим также, что и сами вычисления коэффициентов были проще, чем в общем случае).
нужно решать всего два уравнения с двумя неизвестными (отметим также, что и сами вычисления коэффициентов были проще, чем в общем случае).
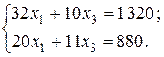
х 3 = 11,59 кН, х 1 = 37,63 кН.
 По полученным значениям основных неизвестных строим окончательную эпюру М (рис.3.8).
По полученным значениям основных неизвестных строим окончательную эпюру М (рис.3.8).
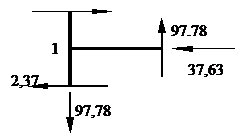
Проще это сделать, сложив грузовую эпюру с исправленными единичными. Проверим равновесие узла 1
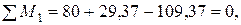 проверка выполняется.
проверка выполняется.
Произведем деформационную проверку, перемножим окончательную эпюру М на первую единичную 


проверка выполняется.
При построении окончательных эпюр поперечных и продольных сил удобнее воспользоваться методом сечений (рис.3.9). Для левой части рамы:

| |||||
| |||||
| |||||


Для правой части рамы:

Например, на участке В-1

Ещё проще определить внутренние усилия на других участках. Окончательные эпюры Q и N изображены на рис.3.10.
 |
Таким образом, имея значения основных неизвестных мы определим внутренние усилия при помощи уравнений равновесия.
Проверим равновесие узла 1: 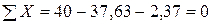 , проверка выполняется.
, проверка выполняется.
Мы не определяли горизонтальные опорные реакции в опорах А и Д. Согласно эпюре N они получились (направления на рис.3.9)
Н А= 42,37; Н D = 37,63
 проверка выполняется.
проверка выполняется.
 | |||
 | |||
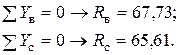
Для всей системы (рис.3.9)

проверка выполняется.
Для расчета различных типов статически неопределимых систем применяют частные методики раскрытия статической неопределимости, удобные для данного типа систем. Расчет при помощи частной методики это тоже расчет методом сил, только не в общей постановке. Будем далее для краткости расчет в общей постановке называть расчетом методом сил, а расчеты при помощи частных методик называть как общепринято.
Пример 1. Жесткий брус АВ (рис.3.11), деформациями которого можно пренебречь, шарнирно закреплен в узле А и удерживается двумя тягами С-1 и С-2.
Определить площадь поперечного сечения F при [σ]=160Мпа.
  |
Расчет методом сил. Система один раз статически неопределима,
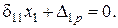 (1)
(1)
Примем в качестве основного неизвестного усилие в тяге С-2. Основная система с неизвестными X1 изображена на рис.3.12. Длины стержней и плечи усилий:


Усилие в стержне С-1 от единичного загружения (рис.3.13)


Усилие в стержне С-1 в грузовом состоянии:


Перемножаем эпюры по правилу Верещагина
|
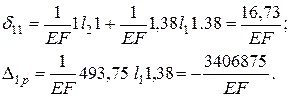
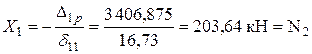 -
-
усилие в стержне С-2.
Усилие в стержне
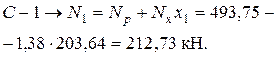
По этому усилию и нужно подобрать поперечное сечение стержня
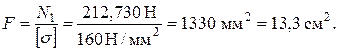
Расчет при помощи уравнения совместности перемещений. Деформированное состояние системы изображено на рис.3.14.

|
Так как брус АВ может только поворачиваться, то из подобия треугольников (А11 и А22)
∆2 = 2∆1. (2)
Это и есть уравнение совместности перемещений. Из треугольников А11 и А22
(так как 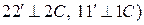 .
.

Подставляем в (2)
 (3)
(3)
По закону Гука
|

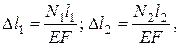
подставляем в (3)

Упрощаем
 (4)
(4)
Составляем дополнительно уравнение равновесия:
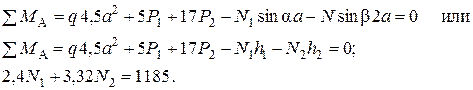
Решение совместно с (4) даёт 
Небольшое несовпадение результатов с расчетом методом сил следует отнести за счёт округления.



 Пример 2. Определить из условий прочности требуемую площадь поперечного сечения F стального бруса (рис.3.15), [δ] = 160 мПа. Построить эпюру продольных
Пример 2. Определить из условий прочности требуемую площадь поперечного сечения F стального бруса (рис.3.15), [δ] = 160 мПа. Построить эпюру продольных
перемещений. Определить наибольшую(по абсолютной
величине) относительную продольную деформацию.
Расчет методом сил. В опорах А и В возникают
опорные реакции, а уравнение равновесия можно
составить лишь одно, поэтому система один раз
статически неопределима

|
Эквивалентная система, единичная и грузовая эпюры продольных сил показаны на рис.3.16.


|
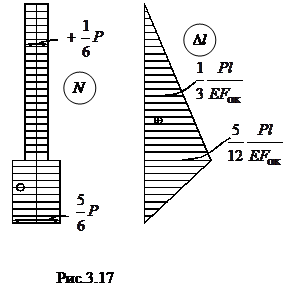
Окончательная эпюра N показана на рис.3.17. Определяем площадь
поперечного сечения F.На верхнем участке

на нижнем участке

Нижний участок наиболее напряжён
 (1)
(1)
Определяем удлинения
участков:
верхнего

среднего

нижнего 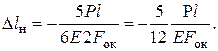
Проверяем условия совместности перемещений

Суммарное удлинение и должно быть равно нулю, так как расстояние АВ неизменно – проверка выполняется. Эпюра продольных перемещений построена рис.3.17.Так как наибольшая интенсивность перемещений на нижнем участке. здесь будет и наибольшая (по абсолютной величине) относительная деформация.

При Р =200 кН из (1)

Решение при помощи уравнения совместности перемещений. Если в заданной системе (рис.3.15) мысленно отбросить верхнее закрепление, заменив реакцией Rа, то суммарное удлинение будет:
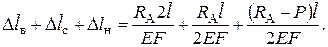
Это суммарное удлинение должно быть равно нулю, так как в заданной системе расстояние АВ неизменно
 (2)
(2)
Это и есть условие совместимости перемещений.
Составляем дополнительно уравнение равновесия
 (3)
(3)
Решение совместно с (2) даёт:

Результат совпадает.
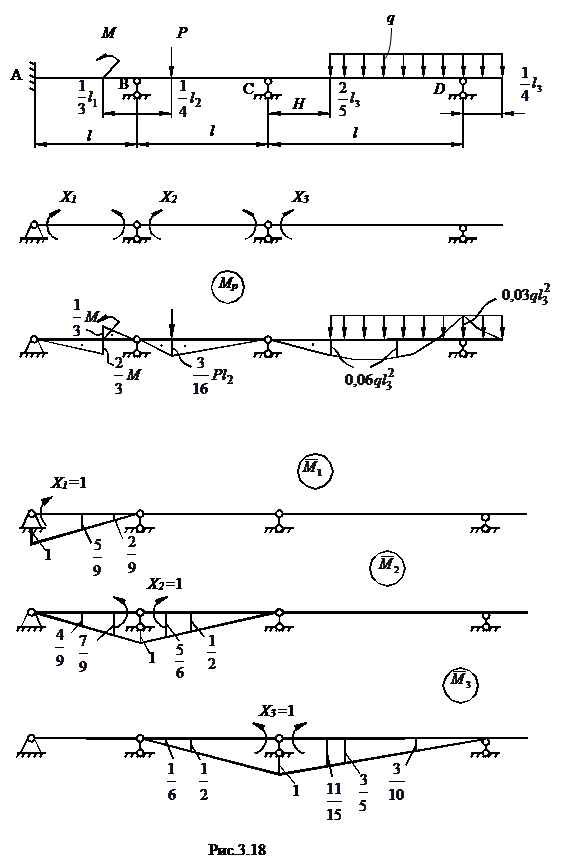
Расчет методом сил. Балка защемлена на опоре А и имеет три шарнирно подвижные опоры, значит она трижды статически неопределима. При выборе основной системы в качестве основных неизвестных приняты изгибающие моменты на опорах. Все эпюры М (грузовая и единичные) в основной системе построены как для простых двухопорных балок. Например грузовая эпюра для балки CD (рис.3.19).
Пример 3. Для неразрезной балки, изображенной на рис.3.18, требуется построить эпюры М и Q и определить величину расчетных усилий.

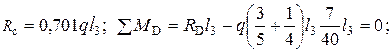
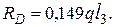

|
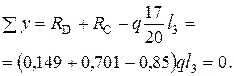
Проверка выполняется.
Коэффициенты при неизвестных и
свободные члены системы уравнений
определяем перемножением эпюр
по правилу Верещагина (на участке
HD
– по формуле Симпсона):
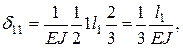

|



Принимаем:

тогда
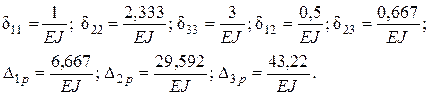
Подставляем эти значения в систему трех уравнений

 х 1 + 0,5 х 2 + 6,667 = 0;
х 1 + 0,5 х 2 + 6,667 = 0;
0,5 х 1 + 2,333 х 2 +0,667 х 3 +29,592 = 0;
0,667 х 2 +3 х 3 + 43,22 = 0.
В результате решения получаем
Х 1 = –2,364 кН∙м, х 2 = −8,605, х 3 = − 12,497.
По этим трем значениям на рис.3.20 изображена эпюра опорных моментов (верхний пунктир). Окончательная эпюра моментов получена сложением этой эпюры с грузовой эпюрой (рис.3.18).
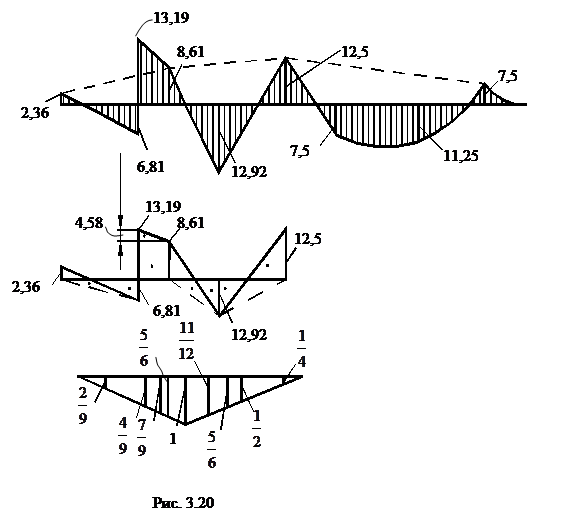
Проведем деформационную проверку, перемножив окончательную эпюру, например, на эпюру 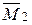 . Для этого соответствующая часть окончательной эпюры и эпюры
. Для этого соответствующая часть окончательной эпюры и эпюры 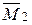 на рис. 3.20 изображены подробнее.
на рис. 3.20 изображены подробнее.

Проверка выполняется. Решение с помощью уравнения трех моментов.

где l n – длина левого от опоры n пролета;  - фиктивная опорная реакция от нагрузок в соседних пролетах поэтому для той же основной системы
- фиктивная опорная реакция от нагрузок в соседних пролетах поэтому для той же основной системы
перестраиваем эпюру Мр
|
нагрузки в пролете СD



|
Приняв эпюру рис.3.21 за нагрузку, определяем фиктивные опорные реакции
Реакция опоры А

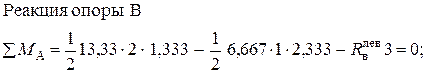

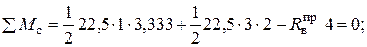





Подставляем эти значения в формулу (1)

2 х 13 + х 23 = – 6 ∙ 6,667;
х 13 +2 х 2 (3+4) + х 3 4 = – 6 ∙ 29,583;
х 2 4 +2х3 (4+5) – 7,5 = – 6 ∙ 45,75.
В результате решения получаем Х1 = – 24,4 кН; х2 = – 8,454, х3 = – 12,953.
Результаты немного отличаются от предыдущих. Строим заново окончательную эпюру моментов (рис.3.22) и производим ту же деформационную проверку
 | |||
|

Проверка выполняется.
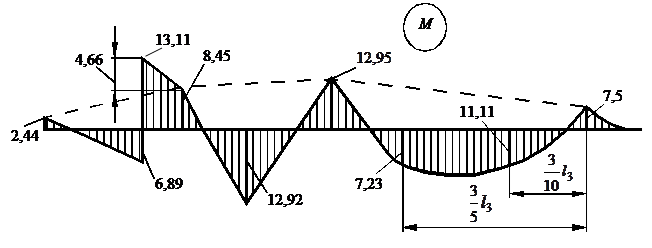
Построим эпюру поперечных сил (рис.3.23), например, по последней эпюре моментов. В первом пролете

или

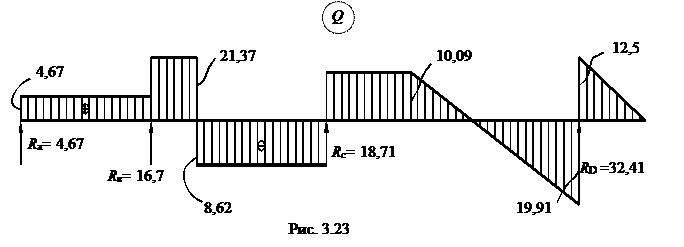
На втором участке
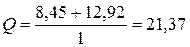 .
.
На третьем участке
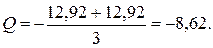
Получим разрыв на эпюре

Проверка выполняется.
На четвёртом участке

На пятом участке от наклона линии, соединяющей значения моментов на границах участка (рис.3,22)



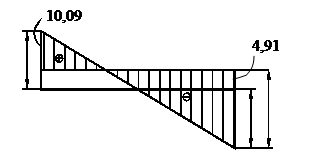
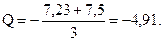
На это значение нужно наложить
эпюру Q в простой балке с L = 3 м

В результате на границе четвёртого и пятого участков не получилось
разрыва, что и должно быть. Проверка выполняется.
Разрывы на опорах – опорные реакции, которые мы отдельно не определяли. Они обозначены на рис. 3.23.
Проверим равновесие всей балки

Проверка выполняется.
Расчётным значением изгибающего момента будет М = 13,11 кНм. Мы не определили максимальное значение момента в третьем пролёте, но оно будет меньше. Расчётным значением поперечной силы будет Q = 21,37 кН. Так как оба эти значения в одном сечении, то другие сечения проверять не нужно.
