- усовершенствования конструкции, технологии изготовления, сборки и испытания машин, обеспечивающих повышение надёжности и безопасности их эксплуатации;
- разработки мероприятий по совершенствованию диагностики, технического обслуживания, повышения качества текущего и капитального ремонтов и снижения затрат на их проведение;
- оптимизации норм расхода запасных частей.
Информация о надёжности машины должна быть:
- достоверной – истинной, правильной, отражающей объёктивные факторы без домыслов и догадок;
- полной – исчерпывающей, содержащей все существенные сведения, которые учитывают при принятии решений;
- однородной – относящейся к одинаковым объектам, эксплуатирующимся в примерно одинаковых условиях;
- дискретной – разделённой по отдельным признакам;
- своевременной, которая может использоваться для изменения конструкций, коррекции технологического процесса изготовления, ремонта и технического обслуживания.
Сбор и анализ информации о надёжности должны проводиться специалистами высокой квалификации, знакомыми с основами теории надёжности и математической статистики, конструкцией, технологией изготовления машин и правилами их технической эксплуатации.
Основные задачи системы сбора и обработки информации:
- определение показателей надёжности машин;
- выявление конструктивных и технологических недостатков машин, приводящих к снижению их надёжности;
- выявление деталей и сборочных единиц, лимитирующих надёжность машины в целом;
- изучение закономерностей возникновения неисправностей и отказов;
- оценка влияния условий и режимов эксплуатации на надёжность машин;
- коррекция нормируемых показателей надёжности;
- обоснование структуры ремонтного цикла и периодичности проведения технического обслуживания и ремонта машин;
- определение эффективности мероприятий по повышению показателей надёжности машин и их элементов.
Сбор и обработка информации о надёжности регламентированы
РД 50-204-87, ГОСТ 27.502-83.
В ходе разработки конструкции информация о надёжности машины поступает из лабораторий, проводящих стендовые испытания опытных образцов, с заводов – изготовителей, полигонов, машиноиспытательных станций и организаций, где машины проходят опытную эксплуатацию.
Важным источником информации о надёжности в гарантийный период эксплуатации машины служат рекламации от потребителей техники.
Основными методами сбора информации о надёжности техники в условиях эксплуатации являются:
Инструментальный метод, который позволяет получить наиболее полный объём объёктивной информации. В качестве технических средств для сбора информации используют специальную контрольно-измерительную аппаратуру и самопишущие приборы, устанавливаемые на исследуемой машине. Надёжность элементов машины оценивается по изменению их технического состояния. Основными недостатками данного метода являются высокая стоимость исследований, ограниченный объём выборки и наблюдаемых машин и организационные трудности, связанные с установкой измерительной аппаратуры и поддержанием её в исправном состоянии.
Метод хронометража применяют для определения чистого времени работы элементов машины, составляющих рабочего цикла машины и оценки использования машины в течении смены, а также показателей безотказности и ремонтопригодности (наработка на отказ, средняя наработка на отказ, средняя наработка до отказа, продолжительность операций технического обслуживания и ремонта и др.). Суть метода заключается в фиксировании моментов начала и окончания работы машины или её отдельных элементов. Для этого метода также можно использовать приборы автоматической регистрации наработки исследуемых элементов машин.
Метод периодических наблюдений пригоден в тех случаях, когда невозможно установить постоянные наблюдения за машиной, например из-за удаленности машины. В таких случаях информацию собирают на основе результатов периодической экспертизы и опроса машинистов с интервалом не более средней наработки на отказ. Основным недостатком метода является недостаточная достоверность результатов.
Метод сбора информации по данным эксплуатационной и ремонтной документации. Основным условием полноты и достоверности информации является добросовестное заполнение технической и учётной документации: журналов учёта наработки, неисправностей машин. Основным недостатком этого метода, как и предыдущего, является низкая достоверность получаемых результатов.
2. Основы теории надёжности
В этом разделе отразить основные положения теории надёжности. Дать понятие комплексного свойства «надёжность» и его составляющих: безотказности, долговечности, ремонтопригодности, сохраняемости. Подробно ответить на вопрос, номер которого указан в знаменателе варианта задания, а название вопроса даётся в приложении 1. Объём раздела 10…12 страниц.
3. Определение числа машин (деталей) в выборке
Показатели надёжности определяются методом выборки. Вследствие значительного рассеяния первичной информации при испытании машин чрезвычайно важно правильно выбрать число одновременно испытуемых машин.
Если число машин при испытании недостаточно, результаты расчёта показателей надёжности будут ошибочны и непригодны для практического использования. Хотя слишком большая повторность испытаний обеспечивает высокую точность расчёта, она неприемлема из-за их высокой стоимости. Поэтому необходимо испытывать такое число машин, при котором получается достаточная точность конечных результатов при невысоких затратах.
Если заранее невозможно предположить, какой теоретический закон распределения использовать, то можно задаться вероятностью безотказной работы машины Р(t), значением доверительной вероятности 
и ориентировочно определить n
n = ln(1 - )/ln Р(t)
- доверительную вероятность = 0,8…0.9 выбирают для машин, неожиданный выход из строя которых не влечёт за собой тяжёлых последствий – человеческих жертв, больших материальных затрат на устранение отказов или потерь от вынужденных простоев. Для машин большой производительности (роторных экскаваторов, самоходных скреперов с ковшом ёмкостью 25 
и др.) = 0,9…0.99.
Для этого можно использовать данные таблицы 2.
Таблица 2 – Определение минимального числа объектов наблюдений при неизвестном законе распределения показателей надёжности
| Р(t) | Значение n при
| |||
| 0,8 | 0,90 | 0,95 | 0,99 | |
| 0,80 | ||||
| 0,90 | ||||
| 0,95 | ||||
| 0,98 | ||||
| 0,99 |
Порядок определения числа объектов наблюдения при неизменном законе распределения следующий:
- задаются установленной в нормативной документации минимальной величиной вероятности безотказной работы Р(t) в течение времени t;
- выбирают значение доверительной вероятности;
- для заданных значений Р(t) по таблице 2 находят число n объектов наблюдений.
В нашем случае число n объектов наблюдений указано в задании. Расчётное значение n сравнить с заданным в варианте и сделать вывод о достаточности количества наблюдений.
По данным выбранного варианта составляется сводная таблица исходных данных (статистический ряд). В неё записываются все измерения в возрастающей последовательности, полученные в процессе исследований (данные из таблицы задания).
4. Среди полученных данных находят максимальное и минимальное измерения: 
и 
. Эти значения являются границами статистического ряда.
5. Определить размах распределения
- .
6. Определить число интервалов. Все измерения от наибольшего до наименьшего разбивают на несколько равных интервалов i. Обычно число интервалов принимают от 5 до 12. При увеличении их числа повышается точность расчётов, но одновременно возрастает их трудоёмкость.
Число интервалов статистического ряда обычно определяется по формуле i = 
± 1,
где n – число испытываемых объектов (число измерений).
Полученный результат округляют до ближайшего большего целого.
7. Определить шаг интервала (длину интервала).
Шаг интервала определяют по формуле
Δt = 
/ i
и округляют в большую сторону.
8. Построить границы интервалов. Для этого необходимо заполнить таблицу 3.
Таблица 3 - Расчёт параметров кривой распределения для n = 70 (пример заполнения таблицы)
| Номер интер- вала i | Границы интерва ла | Среднее значение интерва ла
| Опыт- ная частота
| Опыт-ная
вероят-
ность
| Накоплен
ная опыт ная вероят-
ность
|
|
|
|
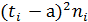
| 25…26 | 25,5 | 0,15 | 0,15 | |||||
| 26…28 | 0,2 | 0,15+0,2= =0,35 | ||||||
| 28…30 | 0,25 | 0,6 | ||||||
| 30…32 | 0,3 | 0,9 | ||||||
| … | … | … | 0.92 | |||||
| 38…40 | 0,03 | 0,95 | ||||||
| 40…42 | 0,05 | 1,0 |
За нижнюю границу первого интервала принимается наименьшее значение статистического ряда в единицах показателя надёжности. Верхней границей первого интервала будет (
). За нижнюю границу второго интервала принимается значение верхней границы первого интервала. Верхней границей второго интервала будет нижняя граница второго интервала (
+ 
, т.е. + 2 
и т.д.. Таким образом заполняются все остальные интервалы. При этом интервалы должны быть одинаковыми по протяжённости. Верхняя граница последнего интервала должна совпасть с максимальным значением статистического ряда или быть несколько больше его, т.к. шаг интервала округляют в большую сторону.
9. Определить среднее значение каждого интервала .
Среднее значение каждого интервала равно сумме значений нижней и верхней границ интервала делённой пополам.
10. Подсчитать число измерений , попадающих в каждый интервал. Для этого из задания выбираем первое измерение (в последовательности по строкам или по столбцам). Смотрим в границы какого интервала это измерение вписывается. Результат записывают в строку соответствующего интервала таблицы 3 (столбец 4). Если измерение попадает на границу интервалов, то оно записывается в интервал с большим номером. В результате все n измерений будут распределены между интервалами. В итоге сумма измерений 
попадающих а интервалы, должна быть равна n. n = 
.
11. Определить опытную вероятность i – го интервала = 
. Результат записать в столбец 5 таблицы 3.
12. Определить накопленную опытную вероятность. Результат записать в столбец 6 таблицы 3.
13. Заполнить столбец 7 таблицы 3для каждого интервала.
14. Определить среднее значение показателя надёжности (математическое ожидание «а» или наработку на отказ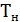 
. а = ).
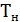Среднее значение показателя надёжности «а» определяется по результатам заполнения столбца 7, по формуле
а = 
· .
15. Определить среднее квадратичное отклонение σ. Для этого выполнить расчёты для остальных столбцов 8 и 9 таблицы 3.
σ – характеристика рассеяния показателя надёжности
σ = 
.
16. Проверка статистического ряда на выпадающие точки.
Собранный статистический ряд может содержать ошибочные измерения, не соответствующие закону распределения случайной величины. Поэтому во время математической обработки статистический ряд проверяют на выпадающие точки.
16.1 Грубую проверку статистики проводят по правилу «трёх сигм» (а±3σ). Расчётным путём получают среднее значение показателя надёжности «а», которое последовательно уменьшают и увеличивают на 3σ. Если крайние измерения статистического ряда не выходят за пределы (а±3σ), то все измерения ряда считаются действительными.
Если появятся выпадающие измерения из статистического ряда, то ряд корректируют и расчёты выполняют заново.
16.2 Более точную проверку статистического ряда даёт проверка по критерию Ирвина λ, теоретическое значение которого приводится в таблице 4 для заданного количества измерений.
Таблица 4 – Критерий Ирвина
| n | |||||||||
| 2,8 | 2,2 | 1,5 | 1,3 | 1,2 | 1,1 | 1,0 | 0,9 | 0,8 |
Расчётное значение критерия выполняется для крайних значений статистического ряда по формуле
= 
,
где 
- крайние соседние точки измерения.
При ≤ - точку считают достоверной.
При 
- точку считают выпадающей и исключают из дальнейших расчётов.
После исключения крайних выпадающих измерений из статистического ряда необходимо повторить расчёты с 3 по 14 пункты задания. Количество интервалов может изменится. Результаты новых расчётов занести в новую таблицу 5 по форме подобной таблице 3, пересчитать математическое ожидание, среднее квадратичное отклонение.
Все расчёты по проверке статистического ряда на выпадающие точки приводятся в пояснительной записке.
Таблица 5 - Расчёт параметров кривой распределения для n = 69
| Номер интер- вала i | Границы интервала | Среднее значение
интервала
| Опытная
частота
| Опытная вероятность Pi (частость) | Накопленная опытная вероятность
|
Pi
|
-a
|
( -a)2
|
| 1500…2139 | 0,06 | 0,06 | -2292 | |||||
| 2139…2778 | 0,01 | 0,07 | -1653 | |||||
| 2778…3417 | 0,17 | 0,24 | -1014 | |||||
| 3417…4056 | 0,22 | 0,46 | -375 | |||||
| 4056…4695 | 0,28 | 0,74 | ||||||
| 4695…5334 | 0,14 | 0,88 | ||||||
| 5334…5973 | 0,12 | 1,00 |
17. Построение гистограммы и определение закона распределения случайной величины
По данным уточнённого статистического ряда (табл.4) строится гистограмма. Для построения гистограммы (рисунок 1) по оси абсцисс откладывают в масштабе границы интервалов t (столбец 2), а по оси ординат - опытные частоты (столбец 3) или опытные вероятности (столбец 5). На её основе строится полигон распределения показателя надёжности. Полигоном распределения называют площадь между ломаной линией, образованной из отрезков, соединяющих середины вершин прямоугольников гистограммы и осью абсцисс.
В
Б
t
А Г
Рисунок 1 – Гистограмма нормального закона распределения
При исследовании надежности машин и их элементов после предварительного анализа результатов наблюдений и гистограммы выдвигают предположение о виде закона распределения значений показателей надёжности. Итак, гистограмма необходима для определения закона распределения, которому подчиняются статистические данные. Характер закона распределения показателей надёжности можно установить по ряду косвенных признаков:
1) По внешнему виду гистограммы, которая даёт наглядное представление об опытном распределении показателя надёжности (рисунок 1 – нормальный закон распределения).
2) По математическому ожиданию и среднему квадратичному отклонению, определённых расчётным (экспериментальным) путём. Если а=σ, то следует воспользоваться экспоненциальным законом распределения. Если а≈σ, то выбирают распределение Пуассона.
3) По коэффициенту вариации V = σ/а:
если V ≤ 0,3 – используется закон нормального распределения;
если V > 0,5 - используется закон распределения Вейбула;
если V = 1,0 - используется экспоненциальный закон распределения.
Если условие выполняется, то гипотеза о предполагаемом законе распределения считается справедливой. Сделать вывод для своего варианта.
18. Построение графиков дифференциальной и интегральной функций.
Для выравнивания распределений показателей надёжности строят теоретическую кривую распределения. В измерениях часто используют нормальный закон распределения.
Нормальный закон распределения характеризуется дифференциальной (функцией плотностей вероятностей) и интегральной (функцией распределения) функциями.
Отличительная особенность дифференциальной функции - симметричное рассеяние частных значений показателя надёжности относительно среднего значения.
Дифференциальную функцию описывают уравнением
= 
,
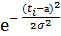где - показатель надёжности.
Если принять а = 0 и σ = 1, то получим выражение для центрированной нормированной дифференциальной функции
= 
.
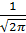
Для определения дифференциальной функции через центрированную нормированную функцию используют уравнение
= 
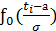(1)
где 
t – шаг (длина) интервала;
- середина i-го интервала;
= 
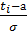- выражение называют квантилем нормального распределения.
Пример: Определим значение дифференциальной функции для первого интервала статистического ряда по (1): t = 639; 
а = 4080.
= 
(
)= 0,65; (-2,3)= 0,65 · 0,03 = 0,02.
По квантилю 
= -2,3 в таблице П1 находим значение дифференциальной функции = 0,03.
Аналогичные расчёты выполним для остальных интервалов. Результаты расчётов сведём в таблицу 5, строка .
Интегральная функция или функция распределения имеет вид
F(t) = 
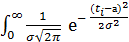dt
при условии а=0 и σ=1 получим центрированную нормированную интегральную функцию
(t) = 
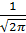
dt (2)
Для определения интегральной функции F(t) через (t) применяют уравнение F(t) = (
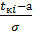), (3)
где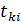 
- значение конца i- го интервала и учитывают (-t) = 1 - (+t)
Пример: Определим значения интегральной функции для первого интервала статистического ряда по (3): а = 4080.
F(1500…2139)= 
(
) = (- 1,97).
(- 1,91) в таблице П2 находим значение интегральной функции.
Для первого интервала
(t) =1- (1,97) =1- 0,97= 0,03
Аналогичные расчёты выполним для остальных интервалов. Результаты расчётов сведём в таблицу 5, строка F(t).
Таблица 5 – Расчёты дифференциальной и интегральной функций
| Интервалы | |||||||
| ƒ(t) | 0,02 | 0,09 | 0,19 | 0,28 | 0,24 | 0,13 | 0,04 |
| F(t) | 0,03 | 0,11 | 0,31 | 0,59 | 0,82 | 0,95 | 0,99 |
На основе полученных значений ƒ(t) и F(t) строят графики дифференциальной (рис.2) и интегральной функций (рис.3). По оси абсцисс откладывают в масштабе значения интервалов статистического ряда, а по оси ординат –
значения ƒ(t) и F(t).
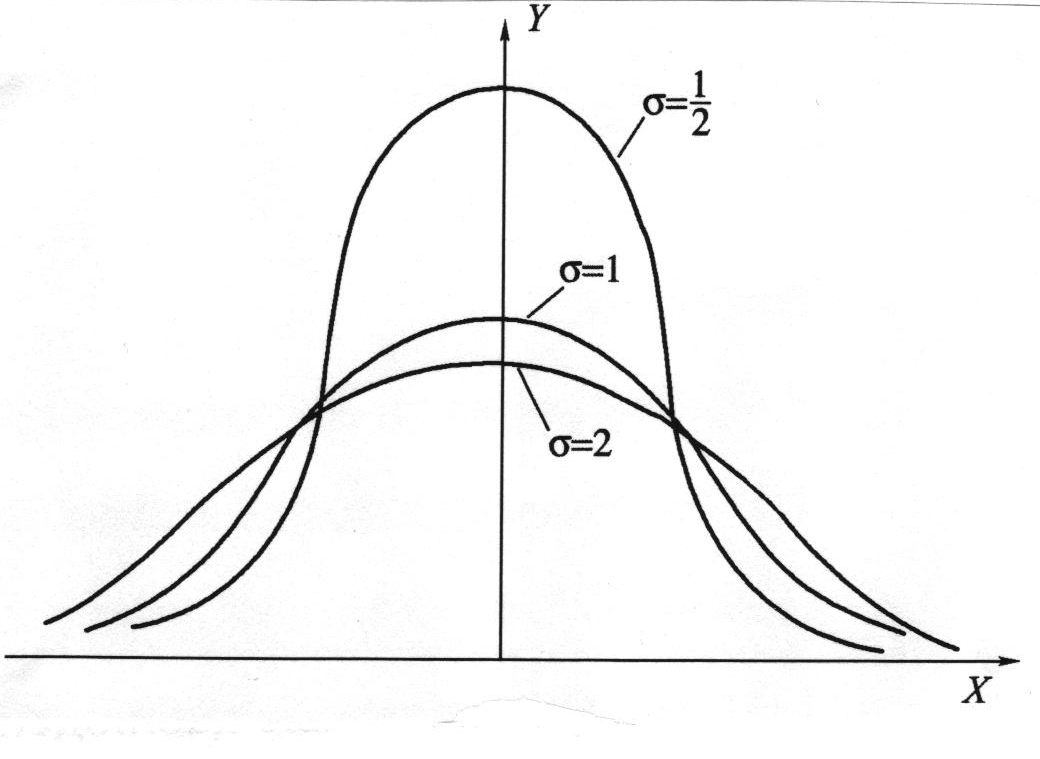
Рисунок 2 - График дифференциальной функций
F(t)
1,0 -…………………………………………….
Рисунок 3- График интегральной функций
Дифференциальная функция нормального распределения заменяет полигон распределения, а интегральная функция нормального распределения - кривую накопленных опытных вероятностей.
19. Определить число двигателей, отказавших в заданном интервале
Для определения числа двигателей, отказавших в интервале заданной наработки, нужно найти отношение площади под дифференциальной кривой, соответствующей этому интервалу, к общей площади под дифференциальной кривой и полученное число умножить на общее число испытуемых двигателей. Однако эта методика сложная.
Число двигателей, отказавших в заданном интервале, с помощью интегральной функции определяют как произведение полученного значения на оси ординат на общее число двигателей.
Для решения практических задач кривая накопленных опытных вероятностей (рис. 4) более удобна, чем полигон распределения.
1,0 …………………………………………………
0,8
0,4
0,2
0
Рисунок 4 - Кривая накопленных опытных вероятностей
Для построения кривой накопленных опытных вероятностей по оси абсцисс откладывают в масштабе показатель надёжности , а по оси ординат соответственно накопленную опытную вероятность . Полученные точки соединяют прямыми. Первую точку соединяют с началом первого интервала. Для каждой наработки можно определить число машин, требующих ремонта. Например, на оси абсцисс находим заданную наработку, а по оси ординат определяем накопленную опытную вероятность (рис. 4) = 0,4. Число неисправных машин (при n = 70 – общее число машин) для заданной наработки будет 
= 0,4 • n = 0,4• 70 = 28 шт.
Тогда вероятность безотказной работы машин для заданной наработки будет Р(t) = 
= 0,6.
20. Определить λ – интенсивность потока отказов. Она обратно пропорциональна наработке на отказ 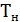= а. λ = 1/ .
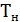Заключение: Обобщить результаты количественных показателей надёжности машины. Оформить пояснительную записку в соответствии с требованиями
[7, 8].
Список литературы
1. Кравченко И.Н. Оценка надёжности машин и оборудования: теория и практика, М., 2012.
2. Шишмарёв В.Ю. Надёжность технических систем, учебник, М., 2010
3. Малофеев С.И. Надёжность технических систем: Примеры и задачи, уч. пос., М.,2010.
4. Фадеев М.А. Элементарная обработка результатов эксперимента, М., 2008.
5. Зорин В.А. Основы работоспособности технических систем, уч., М., 2005.
6. Акимов В.А, и др. Надёжность технических систем и техногенный риск, электронное учебное пос. Режим доступа:www.mchs.gov.ru/library/, М., 2002.
7. 29/13/4 М Е Т О Д И Ч Е С К И Е У К А З А Н И Я к разработке дипломных проектов специальности 170900 Подъемно-транспортные,
строительные, дорожные машины и оборудование (СМ). М., 2002.
8. Боголюбов С.К. Инженерная графика, учебник, М, 2000.
9. О.С.Кузнецова Краткий курс по теории вероятностей и математической статистике: учеб. пособие, - М.: издательство «Окей-книга», 2010.
10. Гриневич Г.П., Каменская Е.А. и др. «Надёжность строительных машин» М., «Прогресс», 1975.
Таблица П 1 Дифференциальная функция (функция плотности вероятности) закона нормального распределения
| Сотые доли | |||||||||
| 0.0 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 |
| 0,1 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,40 | 0,39 | 0,39 | 0,39 | 0,39 |
| 0,2 | 0,39 | 0,39 | 0,39 | 0,39 | 0,39 | 0,39 | 0,39 | 0,39 | 0,39 | 0,39 |
| 0,3 | 0,38 | 0,38 | 0,38 | 0,38 | 0,38 | 0,38 | 0,37 | 0,37 | 0,37 | 0,37 |
| 0,4 | 0,37 | 0,37 | 0,37 | 0,36 | 0,36 | 0,36 | 0,36 | 0,36 | 0,36 | 0,35 |
| 0,5 | 0,35 | 0,35 | 0,35 | 0,35 | 0,35 | 0,34 | 0,34 | 0,34 | 0,34 | 0,34 |
| 0,6 | 0,33 | 0,33 | 0,33 | 0,33 | 0,33 | 0,32 | 0,32 | 0,32 | 0,32 | 0,31 |
| 0,7 | 0,31 | 0,31 | 0,31 | 0,31 | 0,30 | 0,30 | 0,30 | 0,30 | 0,29 | 0,29 |
| 0,8 | 0,29 | 0,29 | 0,29 | 0,28 | 0,28 | 0,28 | 0,28 | 0,27 | 0,27 | 0,27 |
| 0,9 | 0,27 | 0,26 | 0,26 | 0,26 | 0,26 | 0,25 | 0,25 | 0,25 | 0,25 | 0,24 |
| 1,0 | 0,24 | 0,24 | 0,24 | 0,24 | 0,23 | 0,23 | 0,23 | 0,23 | 0,22 | 0,22 |
| 1.1 | 0,22 | 0,22 | 0,21 | 0,21 | 0,21 | 0,21 | 0,20 | 0,20 | 0,20 | 0,20 |
| 1.2 | 0,19 | 0,19 | 0,19 | 0,19 | 0,19 | 0,18 | 0,18 | 0,18 | 0,18 | 0,17 |
| 1,3 | 0,17 | 0,17 | 0,17 | 0,17 | 0,16 | 0,16 | 0,16 | 0,16 | 0,15 | 0,15 |
| 1,4 | 0,15 | 0,15 | 0,15 | 0,14 | 0,14 | 0,14 | 0,14 | 0,14 | 0,13 | 0,13 |
| 1,5 | 0,13 | 0,13 | 0,13 | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 0,11 |
| 1,6 | 0,11 | 0,11 | 0,11 | 0,11 | 0,10 | 0,10 | 0,10 | 0,10 | 0,10 | 0,09 |
| 1,7 | 0,09 | 0,09 | 0,09 | 0,09 | 0,09 | 0,09 | 0,09 | 0,08 | 0,08 | 0,08 |
| 1,8 | 0,08 | 0,08 | 0,08 | 0,08 | 0,07 | 0,07 | 0,07 | 0,07 | 0,07 | 0,07 |
| 1,9 | 0,07 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 |
| 2,0 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 |
| 2,1 | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 |
| 2,2 | 0,04 | 0,04 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 |
| 2,3 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,02 | 0,02 | 0,02 |
| 2,4 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 |
| 2,5 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,01 | 0,01 |
| 2,6 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 |
| 2,7 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 |
| 2,8 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 |
| 2,9 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 |
| 3,0 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
Таблица П 2 Интегральная функция (функция распределения) закона нормального распределения
()
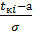| Сотые доли | |||||||||
| 0,0 | 0,50 | 0,50 | 0,51 | 0,51 | 0,52 | 0,52 | 0,52 | 0,53 | 0,53 | 0,54 |
| 0,1 | 0,54 | 0,54 | 0,55 | 0,55 | 0,56 | 0,56 | 0,56 | 0,57 | 0,57 | 0,58 |
| 0,2 | 0,58 | 0,58 | 0,59 | 0,59 | 0,60 | 0,60 | 0,60 | 0,60 | 0,60 | 0,60 |
| 0,3 | 0,62 | 0,62 | 0,63 | 0,63 | 0,63 | 0,64 | 0,64 | 0,64 | 0,65 | 0,65 |
| 0,4 | 0,66 | 0,665 | 0,66 | 0,67 | 0,67 | 0,67 | 0,68 | 0,68 | 0,68 | 0,69 |
| 0,5 | 0,69 | 0,70 | 0,70 | 0,70 | 0,71 | 0,71 | 0,71 | 0,72 | 0,72 | 0,72 |
| 0,6 | 0,73 | 0,73 | 0,73 | 0,74 | 0,74 | 0,74 | 0,75 | 0,75 | 0,75 | 0,76 |
| 0,7 | 0,76 | 0,76 | 0,76 | 0,77 | 0,77 | 0,77 | 0,78 | 0,78 | 0,78 | 0,79 |
| 0,8 | 0,79 | 0,79 | 0,79 | 0,80 | 0,80 | 0,80 | 0,81 | 0,81 | 0,81 | 0,81 |
| 0,9 | 0,82 | 0,82 | 0,82 | 0,82 | 0,83 | 0,83 | 0,83 | 0,83 | 0,84 | 0,84 |
| 1,0 | 0,84 | 0,84 | 0,85 | 0,85 | 0,85 | 0,85 | 0,86 | 0,86 | 0,86 | 0,86 |
| 1,1 | 0,86 | 0,87 | 0,87 | 0,87 | 0,87 | 0,88 | 0,88 | 0,88 | 0,88 | 0,88 |
| 1,2 | 0,89 | 0,89 | 0,89 | 0,89 | 0,89 | 0,89 | 0,90 | 0,90 | 0,90 | 0,90 |
| 1,3 | 0,90 | 0,91 | 0,91 | 0,91 | 0,91 | 0,91 | 0,91 | 0,92 | 0,92 | 0,92 |
| 1,4 | 0,92 | 0,92 | 0,92 | 0,92 | 0,93 | 0,93 | 0,93 | 0,93 | 0,93 | 0,93 |
| 1,5 | 0,93 | 0,93 | 0,94 | 0,94 | 0,94 | 0,94 | 0,94 | 0,94 | 0,94 | 0,94 |
| 1,6 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 |
| 1,7 | 0,96 | 0,96 | 0,96 | 0,96 | 0,96 | 0,96 | 0,96 | 0,96 | 0,96 | 0,96 |
| 1,8 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 |
| 1,9 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,97 | 0,98 | 0,98 |
| 2,0 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 |
| 2,1 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 | 0,98 |
| 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 |
| 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 |
| 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 |
| 2,5 | 0,99 | 0,99 | 0,99 | 0,99 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
Приложение 1