Основные понятия динамики: масса, сила, инерция. Законы Ньютона.
Ма́сса — скалярная неотрицательная релятивистски инвариантная физическая величина, одна из важнейших величин в физике. В нерелятивистском приближении, когда скорости тел много меньше скорости света, определяет их инерционные и гравитационные свойства.
Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений.
Ине́рция — свойство тел оставаться в некоторых системах отсчета в состоянии покоя или равномерного прямолинейного движения в отсутствие или при взаимной компенсации внешних воздействий.
Законы Ньютона:
1. Существуют системы отсчёта (инерциальные), относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел скомпенсированы.
2. Равнодействующая F всех сил, приложенных к телу, ровна произведению массы тела на его ускорение F=ma.
3. Тела взаимодействуют друг с другом с силами, равными по модулю и противоположными по направлению.
Импульс точки, тела. Понятие замкнутой системы материальных точек. Закон сохранения импульса. Общая форма 2 закона Ньютона.
Импульс точки - это физическая векторная величина, которая является мерой действия силы, и зависит от времени действия силы.
Импульс тела - векторная физическая величина, являющаяся мерой механического движения тела.
Системой материальных точек называется совокупность конечного их числа. Силы, с которыми взаимодействуют тела системы называются внутренними. Силы, действующие на систему материальных точек со стороны тел не входят в систему называются внешними. Если на тела не действуют внешние силы, то такая система называется замкнутой или изолированной.
Закон сохранения импульса. Если геометрическая сумма внешних сил действующих на систему равна нулю (система замкнута), то импульс системы сохраняется, то есть не меняется со временем.
 общая форма 2 закона Ньютона
общая форма 2 закона Ньютона
Понятия: работа, мощность, энергия. Работа силы тяжести, силы упругости, силы трения. Консервативные и диссипативные силы. Теорема об изменении кинетической энергии.
Работа есть физическая величина, численно равная произведению силы на перемещение в направлении действия этой силы и ей же вызванное.
Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы.
Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
Работа силы тяжести. Силу тяжести Р материальной точки массой т вблизи поверхности Земли можно считать постоянной, равной mg направленной по вертикали вниз. Работа А силы Р на перемещении от точки М0 до точки М (А=mgh), где h = z0 — zx — высота опускания точки. Работа силы тяжести равна произведению этой силы на высоту опускания (работа положительна) или высоту подъема (работа отрицательна). Работа силы тяжести не зависит от формы траектории между точками М0 и М|, и если эти точки совпадают, то работа силы тяжести равна нулю (случай замкнутого пути). Она равна нулю также, если точки М0 и М лежат в одной и той же горизонтальной плоскости.
Работа линейной силы упругости. Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действующую по закону Гука. (F = - сr), где r — расстояние от точки статического равновесия, где сила равна нулю, до рассматриваемой точки М; с — постоянный коэффициент— коэффициент жесткости. А=--(). По этой формуле и вычисляют работу линейной силы упругости. Если точка М0 совпадает сточкой статического равновесия О, то тогда r0 =0 и для работы силы на перемещении от точки О до точки М имеем (А=-) Величина r — кратчайшее расстояние между рассматриваемой точкой и точкой статического равновесия. Обозначим его λ и назовем деформацией. Тогда (А=-). Работа линейной силы упругости на перемещении из состояния статического равновесия всегда отрицательна и равна половине произведения коэффициента жесткости на квадрат деформации. Работа линейной силы упругости не зависит от формы перемещения и работа по любому замкнутому перемещению равна нулю. Она также равна нулю, если точки Мо и М лежат на одной сфере, описанной из точки статического равновесия.
Работа силы трения. В земных условиях сила трения в той или иной мере проявляется при всех движениях тела. Эта сила возникает лишь при относительном движении соприкасающихся друг с другом тел и направлена противоположно скорости тела. Именно этим она отличается от других сил. Если толкнуть тело, которое лежит на горизонтальной поверхности, то оно будет двигаться против силы трения. Кинетическая энергия при этом уменьшается. Пройдя какое-то расстояние, тело остановится и обратно двигаться не будет. Следовательно, кинетическая энергия, уменьшаясь, в потенциальную не переходит. Можно сделать вывод: если тело движется под действием силы трения, даже в присутствии других сил, то закон сохранения полной механической энергии не выполняется. Полная механическая энергия уменьшается вместе с кинетической энергией.
Силы, действующие в потенциальных полях, называют консервативными. Работа консервативной силы на замкнутом пути равна нулю. Примеры консервативных сил – сила тяжести, сила упругости. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется неконсервативной (или диссипативной). Типичные неконсервативные силы – силы трения.
Теорема об изменении кинетической энергии механической системы формулируется: изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении.
Потенциальная энергия и её связь с работой консервативных сил (сил тяжести и упругости). Закон сохранения энергии в консервативных системах.
,В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0. Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Для консервативных сил выполняются следующие тождества:
— ротор консервативных сил равен 0;
— работа консервативных сил по произвольному замкнутому контуру равна 0;
— консервативная сила является градиентом некой скалярной функции U, называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком. В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды. В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной. Потенциальная энергия — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является Джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными. Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией. Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела. Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой: (Ep = mgh) где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем. Закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механ энергия сохраняется, т.е. не изменяется во времени. Eк + Ep = E = const. Энергия превращается из одного вида в другой. Полная энергия тела- сумма потенциальной и кинетической энергии тела. EK2+EP2=EK1+EP2.
Вращение твёрдого тела вокруг неподвижной оси. Понятие момента инерции точки, тела. Вычисление моментов инерции однородных симметричных тел(стержня, кольца, диска, цилиндра). Теорема Штейнера.
Абсолютно твердое тело – это тело деформацией, которого можно пренебречь. Вращательным называется такое движение, при котором две точки принадлежащие телу остаются все время неподвижными при движении. Прямая проходящая через эти две точки называется осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Тело в этом случае обладает одной степенью свободы, поэтому его положение полностью определяется заданием угла поворота из некоторого начального положения.
Момент инерции материальной точки относительно некоторой оси равен произведению ее массы на квадрат расстояния от точки до этой оси.
J=m умножить на R квадрат.
Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело.
J=Jц. т. +m умножить на S квадрат
ц. т. - центр тяжести.
Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массыdm = dV. Момент инерции тонкого диска. Пусть тонкий однородный диск массыmс концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусыR1иR2. Мысленно разобьём диск на тонкие кольца радиусаr, толщиныdr. Момент инерции такого кольца относительно осиY.

Момент инерции диска: В частности, полагая в (6) R1 = 0, R2 = R,получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси: Момент инерции диска относительно его оси симметрии не зависит от толщины диска. Поэтому по формулам (6) и (7) можно вычислять моменты инерции соответствующих цилиндров относительно их осей симметрии. Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = Jy,а моменты инерции относительно осейXиZравны между собой,Jx = Jz. Поэтому, в соответствии с (3): 2Jx +Jy = 2Jy, Jx = Jy/2
 (6)
(6)
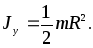 (7)
(7)
 (8)
(8)
Момент инерции цилиндра. Пусть имеется полый симметричный цилиндр массыm, длины h, внутренний и внешний радиусы которого равныR1 и R2. Найдём его момент инерции относительно осиZ, проведенной через центр масс перпендикулярно оси цилиндра (рис. 4). Для этого мысленно разобьём его на диски бесконечно малой толщиныdy. Один из таких дисков, массойdm = mdy/h, расположенный на расстоянииyот начала координат, показан на рис. 4. Его момент инерции относительно осиZ, в соответствии с (8) и теоремой Гюйгенса – Штейнера.  рис4
рис4
 (9)
(9)
 (10)
(10)
Момент инерции цилиндра относительно оси Z(оси вращения маятника) найдём по теореме Гюйгенса – Штейнера
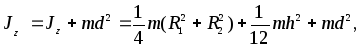
где d– расстояние от центра масс цилиндра до осиZ. В работе 16 этот момент инерции обозначен какJц

Кольца относительно оси, проходящей через его центр и перпендикулярно его плоскости - m*r^2 (m - масса, r - радиус кольца)
Для диска относительно аналогичной оси (m*r^2)/2;
Для стержня через ось, проходящую через него - 0.
Диск относительно диаметра: (m*r^2)/4
Кольцо относительно диаметра: (m*r^2)/2
Стержень относительно оси, перпендикулярной ему и проходящей чере середину: (m*l^2)/12, где l - его длина.
Стержень относительно оси, перпендикулярной ему и проходящей через конец: (m*l^2)/3.
Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции {\displaystyle J} J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела {\displaystyle J_{C}} J_{C} относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела {\displaystyle m} m на квадрат расстояния {\displaystyle d} d между осями.