Каноническое уравнение гиперболического параболоида с полуосями a>0, b>0имеет вид:
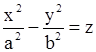 .
.
Исследуем форму гиперболического параболоида. Для построения гиперболического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью XOY. На этой плоскости z=0, поэтому
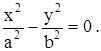
Это уравнение определяет на плоскости пару прямых 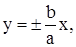 изображенных на рис. 1.8.36.
изображенных на рис. 1.8.36.
Найдем линию пересечения с плоскостью YOZ. На этой плоскости x=0, поэтому 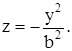
Это уравнение на плоскости YOZ задает параболу, ветви которой направлены вниз (рис. 1.8.36). Сечение плоскостью XOZ также является параболой 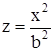 , но ее ветви направлены вверх (рис. 1.8.36).
, но ее ветви направлены вверх (рис. 1.8.36).

Рис.1.8.36.
Найдем линии пересечения поверхности с плоскостью z=-h, h>0. Уравнения этой линии:
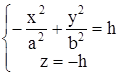 .
.
Первое уравнение преобразуем к виду:
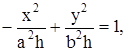
то есть к виду:
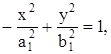
где 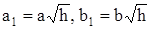 .
.
Данное уравнение является уравнением гиперболы.
Ее действительная ось параллельна оси OY, а мнимая – оси OX. Полуоси равны соответственно 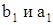 (рис. 1.8.37).
(рис. 1.8.37).
Найдем линии пересечения с плоскостями 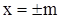 , параллельными плоскости YOZ. Уравнения этих линий:
, параллельными плоскости YOZ. Уравнения этих линий:
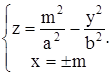
Первое из этих уравнений является уравнением параболы, такой же, как и в сечении плоскостью x=0, только сдвинутой вдоль оси OX на величину 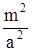 вверх.
вверх.
Эти параболы изображены на рисунке 1.8.37.

Рис.1.8.37.
Так как m - произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости x=0.
Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости YOZ, а вершина скользила по параболе в плоскости y=0.
Плоскость z=h>0, пересекает поверхность по гиперболе, но в отличие от гиперболы в плоскости z=-h<0, ее действительная ось параллельна теперь оси OX, а мнимая- оси OY(рис. 1.8.38).
Гиперболический параболоид изображен на рисунках 1.8.39, 1.8.40.

Рис. 1.8.38.
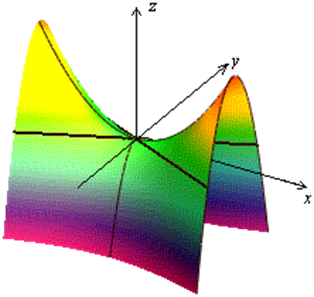
Рис1.8.39.
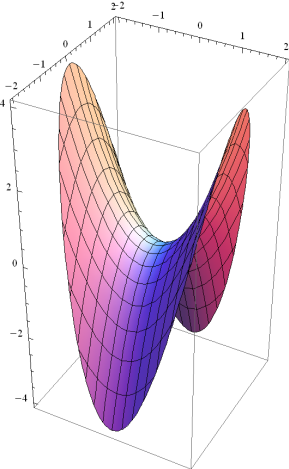
Рис.1.8.40.
Цилиндры
Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые - образующими.
Рассмотрим уравнение вида F(x;y)=0. В это уравнение не входит явно переменная-z. Покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси OZ. Ему будут удовлетворять координаты всех точек 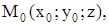 , где z - любое число.
, где z - любое число.
Следовательно, при любом точка M лежит на поверхности, определяемой этим уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку параллельно оси OZ. А это означает, что поверхность, определяемая уравнением, составлена из прямых, параллельных оси OZ, то есть она является цилиндрической поверхностью.
Заметим, что на плоскости уравнение F(x;y)=0 определяет направляющую рассматриваемой цилиндрической поверхности.
Итак, если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Для того чтобы построить поверхность, задаваемую уравнением F(x;y)=0, достаточно изобразить на плоскости направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси OZ.
Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости XOY.
В каждом таком сечении получим такую же кривую, как и исходная направляющая.
а) эллиптический цилиндр (рис.1.8.41, 1.8.42, 1.8.43):
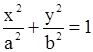 .
.
(
Рис.1.8.41.
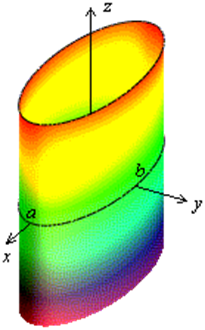
Рис.1.8.42.
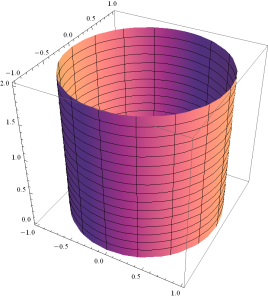
Рис.1.8.43.
б) гиперболический цилиндр 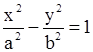 (рис. 1.8.44,1.8.45,1.8.46):
(рис. 1.8.44,1.8.45,1.8.46):
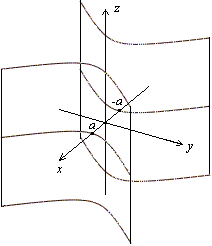
Рис.1.8.44.
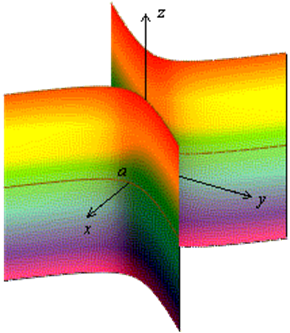
Рис.1.8.45.
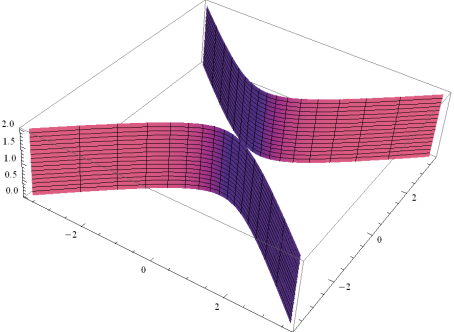
Рис.1.8.46.
с) параболический цилиндр (рис.1.8.47, 1.8.48, 1.8.49):
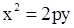 или
или 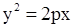 .
.

Рис.1.8.47.
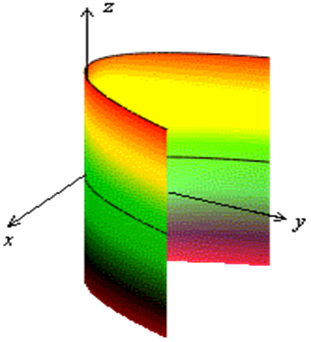
Рис.1.8.47.
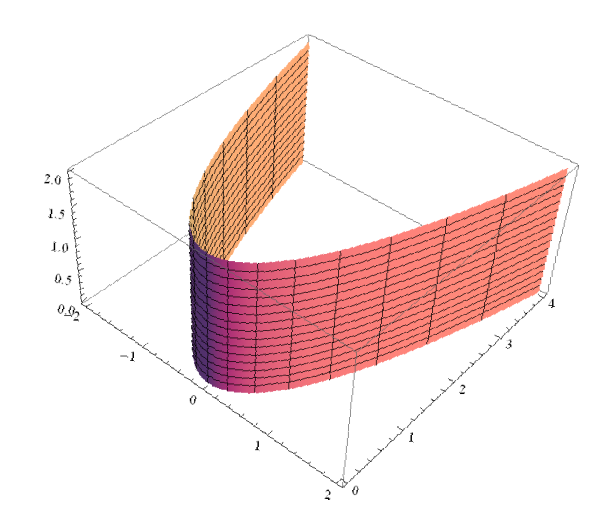
Рис.1.8.49.
Пример.
Привести к канонгическому виду уравнение поверхности второго порядка. Указать тип. Поверхности.
Решение.
Выделяем полные квадраты для переменных x, y, z.
3x2 -9y2-4z2-6x-18y+16z-58=0.
Группируем слагаемые:
3(x2-2x)-9(y2+2y)-4(z2-4z)-58=0
3(x2-2x+1)-9(y2-+2y+1)-4(z2-4z+4)-3+9+16-58=0
3 (x-1)2 – 9 (y+1)2 - 4(z2-2)2 = 36
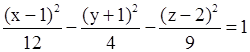
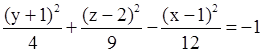 /
/
Данное уравнение согласно классификации поверхностей второго порядка п.1.8.5 является уравнением двуполостного гиперболоида.