1. Умение: Применять понятие рационального числа.
Понятие: Рациональным называется число, которое можно записать в виде 
, где а – целое число, а n – натуральное.
Свойства: 1) Любое целое число а является рациональным, так как его можно записать в виде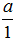 
.
2) Сумма, разность и произведение рациональных чисел – тоже рациональное число.
3) Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
4) Любое рациональное число можно записать либо в виде десятичной, либо в виде периодической дроби.
Пример 1: Представьте в виде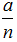 
(где а – целое число, а n – натуральное) произведение 
.
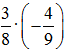Решение:
.
Ответ: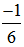 
.
Пример 2: Выразите в виде десятичной или периодической дроби числа: а)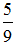 
; б) 5 
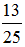; в)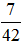 
.
Решение: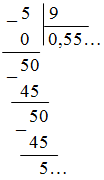 
= 0, (5)
б) 
= 5,52;
в)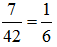 
= 0,1(6).
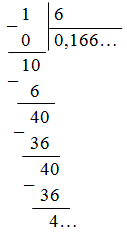
Ответ: а) 0,(5); б) 5,52; в) 0,1(6).
2. Умение: Применять переместительный и сочетательный законы сложения рациональных чисел.
Правило: Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Если а, b и с – любые рациональные числа, то
а + b = b + a;
а + (b + c) = (a + b) + c;
a + 0 = a;
a + (– а) = 0.
Пример 1: Сложив сначала противоположные числа, найдите значение выражения: 259 – 643 – 372 – 259 + 643.
Решение: Сумма противоположных чисел равна нулю, значит:
259 + (–259) = 0
–643 + 643 = 0
259 – 643 – 372 – 259 + 643 = –372.
Ответ: –372.
Пример 2: Упростите выражение: 3,7 – а + 2,9 + b – 7,63 + а – b.
Решение: Выделим противоположные числа и сгруппируем слагаемые:
3,37 – а – 2,9 + b – 7,63 + а – b = 3,37 – 2,9 + 7,63 = (3,37 + 7,63) –
– 2,9 = 11 – 2,9 = 8,1.
Ответ: 8,1.
3. Умение: Применять переместительный, сочетательный и распределительный законы умножения рациональных чисел.
Правило: Если а, b и с – любые рациональные числа, то
а · b = b · a;
а · (b · c) = (a · b) · c;
a · 1 = a; а · 
= 1; а ¹ 0;
а · 0 = 0;
а · b = 0, если а = 0 или b = 0;
(а + b) · с = ас + bc.
Пример: Выбирая удобный порядок вычислений, найдите значение выражения:
а) –4 · 16 · 25 · (–9);
б) 7,2 · (–0,4) + 2,8 · (–0,4);
в)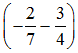 
· (–28).
Решение:
а) –4 · 16 · 25 · (–9) = (–4 · 25) · (16 · (–9)) =
= –100 · (–144) = 144 · 100 = 14400;
б) 7,2 · (–0,4) + 2,8 · (–0,4) = (7,2 + 2,8) · (–0,4) = 10 · (–0,4) =
= – (0,4 · 10) = –4;
в) 
8 + 21 = 29.
Ответ: а) 14400; б) –4; в) 29.
4. Умение: Раскрывать скобки в выражении.
Правило: 1) Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».
2) Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки слагаемых:
–(а + b) = – а – b.
3) Чтобы раскрыть скобки, перед которыми стоит знак «–», надо изменить этот знак на «+», поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Пример 1: Найдите значение выражения, раскрыв предварительно скобки:
а) 5,9 – (7,3 – 8,1);
б) (3,52 – 2,63) – (4,02 + 3,13).
Решение:
а) 5,9 – (7,3 – 8,1) = 5,9 + (–7,3 + 8,1) = 5,9 – 7,3 + 8,1 = 5,9 + 8,1 –
– 7,3 = 14 – 7,6 = 6,7;
б) (3,52 – 2,63) – (4,02 + 3,13) = 3,52 – 2,63 + (–4,02 – 3,13) =
= 3,52 –2,63 – 4,02 – – 3,13 = 3,52 – 4,02 – 2,63 – 3,13 = – 1,5 – 2,63 –
– 3,13 = –4,13 – 3,13 = –4,13 + (–3,13) = – (4,13 + 3,13) = –7,26.
Ответ: а) 6,7; б) –7,26.
Пример 2: Упростите выражение m – (13 + m).
m – (13 + m) = m + ( –13 – m) = m – 13 – m = –13.
5. Умение: Находить числовой коэффициент произведения и приводить подобные слагаемые.
Определение 1. Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом (или просто коэффициентом).
Определение 2. Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Правило: Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Пример 1: Найдите коэффициент произведения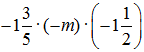 
.
Решение: Перемножим числа, входящие в запись выражения:
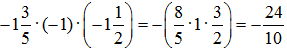= –2,4.
Ответ: –2,4.
Пример 2: Упростите выражение 7 х + 18 у – 14 х +32 у –13 у.
Решение: 7 х + 18 у – 14 х +32 у –13 у = 7 х – 14 х + 18 у + 32 у – 13 у =
= х · (7 – 4) + у (18 + 32 – 13) = 3 х + 47 у.
Ответ: 3 х + 47 у.
6. Умение: Решать уравнения.
Правила преобразования уравнений:
1) Корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число, отличное от нуля.
2) Корни уравнения не изменятся, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
Определение: Уравнение вида ах = b, где а ¹ 0, называется линейным уравнением с одним неизвестным.
Алгоритм решения линейного уравнения:
1. Если необходимо избавиться от дробных коэффициентов, умножаем обе части уравнения на их общий знаменатель.
2. Переносим все слагаемые с переменной в левую часть уравнения, а без переменной – в правую, меняя знаки переносимых слагаемых на противоположные.
3. Приводим подобные слагаемые в обеих частях уравнения.
4. Решаем полученное уравнение ах = b, где а ¹ 0, делением обеих частей уравнения на а.
Пример: Решите уравнения.
а) 3 х = 12; б) 2 х – 14 = 0;
в) 3 х + 18 = 2 х – 11; г) –3 х – 22 = 7 х – 11;
д) 
; е) 
.
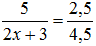Решение: а) 3 х = 12 |: 3
х = 4
б) 2 х – 14 = 0 в) 3 х + 18 = 2 х – 11
2 х = 14 |: 2 3 х – 2 х = –11 – 18
х = 7 х = –29
г) –3 х – 22 = 7 х – 11 д) 
· 8
–3 х – 7 х = –11 + 22 6 у – 100 = 9 у –1
–10 х = 11; |: (–10) 6 у – 9 у = –1 + 100
х = 
–3 у = 99; |: (–3)
х = –1,1 у = –33
е) 
. Используем основное свойство пропорции:
5 · 4,5 = (2 х + 3) · 2,5 |: 2,5
2 · 4,5 = 2 х + 3
9 = 2 х + 3
–2 х = 3 – 9
–2 х = –6 |: (–2)
х = 3
Ответ: а) 4; б) 7; в) –29; г) –1,1; д) –33; е) 3.
7. Умение: Решать задачи с помощью линейных уравнений.
Алгоритм решения задачи:
1. Анализируем условие задачи, выделяя известные и искомые величины, а также зависимости между ними. Результат анализа представляем в виде схемы, таблицы, наброска и т. д.
2. Обозначаем за х неизвестную величину и, используя зависимости, составляем уравнение.
3.Решаем полученное уравнение и записываем ответ задачи. Если за х обозначаем не главную искомую величину, то проводим дополнительные вычисления.
Пример: Решите задачу.
На первую автомашину погрузили на 0,6 т зерна больше, что на вторую. Если бы на первую автомашину погрузили в 1,2 раза больше, а на вторую в 1,4 раза больше, то груза на обеих машинах было бы поровну. Сколько тонн груза погрузили на каждую автомашину?
Решение: Схематично изобразим распределение груза по автомашинам в первом и втором случае в виде таблицы.
Пусть х т груза было во второй машине первоначально, тогда х +
+ 0,6 т – было в первой машине. Тогда 1,2 · (х + 0,6) и 1,4 х т груза стало в первой и второй машине соответственно во втором случае. Зная, что груза в автомашинах стало поровну, составим уравнение:
1,2 · (х + 0,6) = 1,4 · х
1,2 х + 1,2 · 0,6 = 1,4 х
1,2 х + 0,72 = 1,4 х
1,2 х – 1,4 х = –0,72
–0,2 х = –0,72; |: (–0,2)
х = 3,6
Значит, 3,6 т груза погрузили на вторую машину.
3,6 + 0,6 = 4,2 т груза погрузили на первую машину.
Ответ: 4,2 т; 3,6 т.
8. Умение: Применять понятие параллельных и перпендикулярных прямых; использовать координатную плоскость при решении задач.
Определение 1: Две непересекающиеся прямые на плоскости называются параллельными.
Обозначение: а || b.
Свойства: 1) Если две прямые в плоскости перпендикулярны третьей, то они параллельны.
2) Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Определение 2: Системой координат на плоскости называется пара перпендикулярных координатных прямых х и у, которые пересекаются в начале отсчета – точке О.
Определение 3: Пусть М – произвольная точка плоскости. Она имеет координаты М (х 0; у 0), где х 0 – абсцисса точки М, у 0 – ордината.
Правило нахождения координат точки:
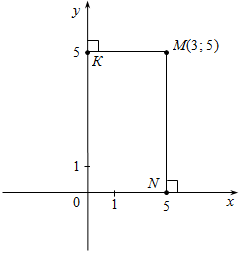
| MN – перпендикулярная оси х. МК – перпендикулярная оси у. |
Пример 1:Постройте точки А (2; 4); В (–3; 2); С (–1; –5).
Решение:
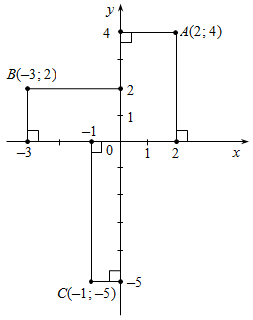
Пример 2:Среди точек А, В, С и D, изображенных на рисунке, найдите точки с противоположными абсциссами. Есть ли среди прямых АВ, ВС, СD и АD – параллельные?
Решение: 1) Определим координаты точек: А (–4; 5); В (3; 5); С (4; –3); D (–4; –3).
Противоположные абсциссы имеют точки А и С и С и D.
2) АВ || Ох, так как А и В имеют равные ординаты.
DC || Ох, так как D и С имеют равные ординаты.
Значит, АВ || DC.
Ответ: 1) А и С; С и D; 2) АВ || DC.
9. Умение: Применять столбчатые и круговые диаграммы и графики при решении задач.
Правило: Распределение числового значения некоторых величин удобно представлять в виде столбчатых или круговых диаграмм.
Пример 1: В классе 28 учеников. В таблице представлены результаты годовой контрольной по математике.
| Отметка | «2» | «3» | «4» | «5» |
| Количество учеников |
Изобразите распределение учеников по полученным отметкам в виде столбчатой и круговой диаграмм.
Решение: 1)
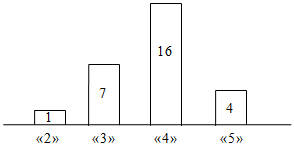
2) Для построения круговой диаграммы разделим круг на 4 сектора пропорционально количеству учеников, получивших определенную отметку:
«2»  ≈ 0,04 круга;
«3»  ≈ 0,25 круга;
«4» 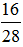 ≈ 0,6 круга;
«5»  ≈ 0,11 круга.
| 
|
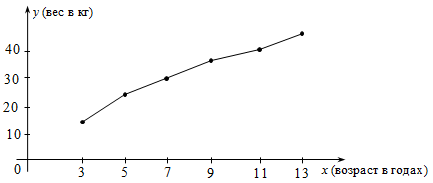
Пример 2: Постройте график зависимости веса Марины от ее возраста по следующим данным:
| Возраст (в годах) | ||||||
| Вес (кг) |
Решение:
