Рассмотрим на примере процедуру составления спецификации эконометрической модели.
Пример.
Экономическими переменными равновесного рынка являются: Yd — спрос на товар данного вида, Ys — предложение товара, р — рыночная цена товара (цена равновесия). Из экономической теории известно, что переменные Yd, Ys, р, взаимосвязаны: величина спроса зависит от цены (спрос на товар с ростом цены убывает); величина предложения зависит от цены (предложение товара с ростом цены возрастает); цена товара на конкурентном рынке зависит от величин спроса Yd и предложения Ys (равновесная рыночная цена формируется в результате равенства спроса и предложения). Формально, перечисленные выше закономерности, можно записать следующим образом:
Yd = d(p) —функция спроса,
Ys = s(p) — функция предложения, (1.13)
р = f(Yd,Ys) — реакция рынка.
Однако для прогнозирования или оценки значений экономических переменных недостаточно только предположений. Система (1.13) не отражает законов, по которым можно судить о степени взаимосвязи между переменными, о скорости возрастания или убывания спроса и предложения в зависимости от цены. Для анализа этих процессов необходимо построить экономико-математическую модель.
Определение 1. Экономико-математическая модель объекта (математическая модель экономического объекта) представляет собой математически выраженную связь между его экономическими переменными. Это либо набор графиков или таблиц, либо система математических уравнений (алгебраических, конечно-разностных, дифференциальных, интегральных и т. д.) и, возможно, неравенств, связывающих воедино экономические переменные объекта [2]. Для построения экономико-математической модели объекта необходимо формализовать (описать на математическом языке) экономические законы о взаимосвязи его экономических переменных (соотношения). Выберем в качестве функции спроса и предложения, для простоты, подходящие линейные функции:
Yd = а0 + а1 р, где а1 < 0;
Ys =bQ+b1 р, где b 1 > 0.
С учетом этого факта получаем спецификацию экономико-математической модели спроса и предложения на конкурентном рынке:
Y d = а0+ а1∙р, а1 < 0,
Ys =bQ+b1 р, где b 1 > 0, (1.14)
Y d = Ys
Модель содержит три искомые экономические переменные (Yd, Ys, р) и такое же количество алгебраических уравнений. Система (1.14) получена в результате математической формализации закономерностей общей экономической теории — это первый принцип составления спецификации модели.
Модель (1.14) предназначена для оценки трех эндогенных переменных (Yd, Ys, р), в ней отсутствуют экзогенные переменные. Однако из общей экономической теории известно, что величина дохода потребителя (х) представляет собой главный неценовой фактор спроса, поэтому, для уточнения спецификации модели, включим данный фактор в первое уравнение системы (1.14):
Y d = а0+ а1 р+ а2 х, а1 < 0, а2 >0,
Ys =b0+b1 р, b 1 > 0 (1.15)
Y d = Y s.
Система (1.15) представляет собой спецификацию традиционной экономической модели спроса и предложения на конкурентном рынке. Она используется для описания состояния равновесия на рынке товаров первой необходимости. Проанализируем спецификации (1.14) и (1.15). Они содержат три уравнения и три определяемые переменные Yd, Y s и р. Однако в спецификации (1.15) присутствует переменная х, которая задаётся вне модели и является экзогенной переменной.
Определение 2. При наличии хотя бы одной экзогенной переменной модель называется открытой, в противном случае — замкнутой. В соответствии с данным определением, модель со спецификацией (1.14) — замкнутая модель, со спецификацией (1.15) — открытая. В правильно составленной спецификации содержится столько уравнений, сколько эндогенных переменных включается в модель — это второй принцип спецификации.
Третий принцип спецификации — учет фактора времени в экономических моделях, или датирование экономических переменных. В системе (1.15) предполагается, что спрос и предложение мгновенно реагируют на изменение цены, т.е. в моделях не учитывается фактор времени t. Однако, как следует из экономической теории, экономический объект обладает той или иной степенью инерционности и, как правило, меняется во времени. Так, например, цена р товара со временем меняется, причем предложение реагирует на изменение цены с некоторым запаздыванием. Поэтому в данном случае включение в модель фактора времени позволяет сделать модель более адекватной действительности. Зависимость от времени переменных Yd,Ys,р,х принято обозначать следующим образом:
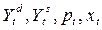
где t — текущий момент времени, к которому относятся эти величины.
Определение 3. Переменные модели называются датированными, если обозначена их зависимость от времени. Если экономические утверждения отражают статическую (относящуюся к одному периоду времени) взаимосвязь всех включённых в модель переменных, то значения таких переменных принято называть пространственными данными. И надобности в их датировании нет. Если экономические утверждения отражают динамическую (зависящую от фактора времени) взаимосвязь включённых в модель переменных, то значения таких переменных датируют и называют динамическими или временными рядами [9, с. 16]. Датируем переменные модели (1.3) с учетом экономических предпосылок
Ytd = а0 + а1∙ рt + а 2∙ хt, а1 < 0, а 2 > 0,
Yts =b 0 +b1 ∙ рt-1, b1 > 0, (1.16)
Y d =Y s,
Данная модель получила название расширенной «паутинной» модели. В уравнении предложения данной модели присутствует переменная, значения которой относятся к предыдущему моменту времени. В такой ситуации говорят, что в модели выбран лаг в один период.
Определение 4. Лаговыми называются экзогенные или эндогенные переменные экономической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Модели, включающие лаговые переменные, относятся к классу динамических моделей Обычно в экономических моделях объединяют переменные, значения которых известны к текущему моменту времени t, в отдельную группу экономических переменных. Переменные такой группы называются предопределёнными. Так, в модели (1.16) предопределёнными являются переменные (хt, рt-1).
Определение 5. Предопределёнными называются лаговые и текущие экзогенные переменные.
Основная цель построения экономических моделей — оценка (или прогнозирование) текущих значений эндогенных переменных по значениям предопределенных переменных, т. е. предопределенные переменные в экономических моделях используются в качестве объясняющих переменных. Так, например, расширенная «паутинная» модель (1.16) создаётся для оценки (прогноза) текущих эндогенных переменных Ytd, Yts, pt по значениям предопределённых переменных (хt, рt-1).
Четвертый принцип спецификации — включение случайных возмущений в спецификацию экономической модели. Несмотря на проведенные уточнения спецификации (списка переменных модели, взаимосвязи между эндогенными и предопределенными переменными), рассмотренные варианты спецификаций модели равновесного рынка обладают недостатком, которым обладают все экономические модели — неадекватность объектам-оригиналам. На практике не всегда удается учесть влияние всех факторов на изучаемую переменную (например, в функции спроса учесть национальные и возрастные особенности потребителя, их индивидуальность и др.), выбрать правильную форму математической зависимости между экономическими переменными (например, нелинейную вместо линейной), безошибочно выполнить измерения (правильно провести опрос, выполнить агрегирование значений переменных). Поэтому эндогенные переменные модели следует рассматривать как случайные величины и, помимо детерминированной составляющей, описывающей поведение эндогенной переменной в зависимости от предопределенных переменных, включать некоторые случайные величины, называемые случайными возмущениями (случайными ошибками). Уточним спецификацию модели (1.16) путем включения случайных возмущений:
Ytd = а0 + а1∙ рt + а 2∙ хt + vt, а1 < 0, а 2 > 0,
Yts =b 0 + b1 ∙ рt-1 + wt, b1 > 0, (1.17)
Y d =Y s.
Случайные возмущения v, и w добавляются в поведенческие уравнения (уравнения, описывающие поведение эндогенных переменных в зависимости от предопределенных и включающие параметры), и не добавляются в уравнения тождества. Спецификация (1.17) неполная. Включая случайные величины в модель, необходимо принять предпосылки об их основных количественных характеристиках.
Экономические модели со случайными возмущениями принято называть эконометрическими. Эконометрические модели адекватнее описывают экономические объекты и позволяют, в отличие от экономических, используя аппарат теории вероятностей и математической статистики, выполнить оценку точности результатов прогнозирования и (или) оценивания значений эндогенных переменных.
Второе уравнение из спецификации модели (1.7) можно записать в виде
Yts =b 0 + b1 ∙ рt-1 + wt (1.18)
E (wt|рt-1 )=0
E (w 2 t|рt-1 )=σ2 w
В первом уравнении (1.18) случайная величина wt отражает влияние на текущую эндогенную переменную Ytd не определенных в модели факторов. Во втором уравнении спецификации постулируется, что при каждом фиксированном значении рt-1 случайное возмущение wt имеет нулевое ожидаемое значение. Наконец, третье уравнение спецификации (1.18) отражает весьма жесткое предположение, что средний квадрат разброса значений wt вокруг нуля сохраняется неизменным (хотя и неизвестным) при любом фиксированном значении предопределенной переменной G t-1. В эконометрике случайные возмущения с таким свойством именуются гомоскедастичными.
Замечание. Гипотеза о гомоскедастичности возмущения, заложенная в третьем уравнении (1.18), может и не соответствовать реальности. Тогда ее легко отбросить и заменить предпосылкой:
E(w2t |рt- 1) = σ20 р λt -1
где λ - некоторое действительное число, а σ0 — некоторое положительное число.
Это означает, что средний квадрат разброса значений wt вокруг нуля является степенной функцией уровня цены товара рt- 1 в предыдущем периоде. Экономисты именуют такое случайное возмущение wt гетероскедастичным.
См. дополнительно литературу: [1, с. 69-71]; [2, с. 66 - 117]; [8]; [9].