Линии второго порядка
Основные вопросы:
1. Основные понятия.
2. Окружность.
3. Эллипс.
4. Гипербола.
5. Парабола.
6. Общее уравнение линий второго порядка.
ОСНОВНЫЕ ПОНЯТИЯ
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
.
Коэффициенты уравнения – действительные числа, но, по крайней мере, одно из чисел 
отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.
ОКРУЖНОСТЬ
Простейшей кривой второго порядка является окружность.
Определение. Окружностью радиуса R с центром в точке 
называется множество всех точек 
плоскости, удовлетворяющих условию 
.
Каноническое уравнение окружности 
.
Эллипс
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Каноническое уравнение эллипса 
.
у
b М
r 1 r 2
–а с а
F 1 O F 2 х
–b
F 1, F 2 – фокусы, F 1 (– c; 0); F 2(c; 0)
с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.
МF 1 =r 1, МF 2 =r 2.
и 
называются фокальными радиусами. 
, 
По определению эллипса r 1 +r 2=2 а.
Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
a 2 = b 2 + c 2.
Определение. Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет – величина, определяемая отношением: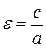 
.
Замечание. Для эллипса 
.
Определение. Прямые 
называются директрисами эллипса.
Теорема. Если 
– расстояние от произвольной точки эллипса до какого-нибудь фокуса,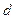 
– расстояние от этой же точки до соответствующей этому фокусы директрисы, то отношение 
есть постоянная величина, равная эксцентриситету эллипса: 
.
Замечание. Если a = b, то c = 0, а значит, фокусы сливаются, и эллипс превращается в окружность.
Если же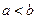 
, то уравнение определяет эллипс, большая ось которого 
лежит на оси Оу, а малая ось 
– на оси Ох. Фокусы такого эллипса находятся в точках F 1 (0;с); F 2(0;-с), где b 2 = a 2 + c 2.
Пример. Составьте уравнение эллипса, если его фокусы F 1(0; 0), F 2(1; 1), а большая ось равна 2.
Уравнение эллипса имеет вид: 
.
Расстояние между фокусами: 2 c = 
, таким образом,
a 2 – b 2 = c 2 = 
.
По условию большая ось равна 2, то есть 2 а = 2, откуда получаем, что
а = 1, b = 
.
Тогда искомое уравнение эллипса имеет вид: 
.
Гипербола
Определение. Гиперболой называется линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы 
.
y
M (x, y)
b
r 1
r 2
x
F 1 a F 2
c
По определению
ï r 1 – r 2ï= 2 a.
F 1, F 2 – фокусы гиперболы.
F 1 F 2 = 2 c.
Теорема. Фокусное расстояние и полуоси гиперболы связаны соотношением:
c 2 = a 2 + b 2
Ось 2 а называется действительной осью гиперболы.
Ось 2 b называется мнимой осью гиперболы.
Прямоугольник со сторонами 2 а и2 b называется основным прямоугольником гиперболы.
Гипербола имеет две асимптоты, уравнения которых 
Замечание. Для гиперболы эксцентриситет 
.
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a /ε от него, называются директрисами гиперболы. Их уравнения: 
.
Определение. Гипербола называется равносторонней, если ее полуоси равны (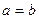
).
Ее каноническое уравнение 
.
Определение. Эксцентриситетом гиперболы называется отношение расстояние между фокусами к величине действительной оси гиперболы, обозначается 
: 
.
Кривая, определяемая уравнением 
, также есть гипербола, действительная ось которой расположена на оси 
, а мнимая ось – на оси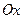 
.
Гиперболы и 
имеют общие асимптоты. Такие гиперболы называются сопряженными.
Пример. Составьте уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса, заданного уравнением 
Найдем фокусное расстояние для эллипса:
c 2 = 25 – 9 = 16.
Для гиперболы:
c 2 = a 2 + b 2 = 16, ε = c / a = 2; c = 2 a; c 2 = 4 a 2; a 2 = 4; b 2 = 16 – 4 =12.
Тогда искомое уравнение гиперболы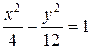 
.
Парабола
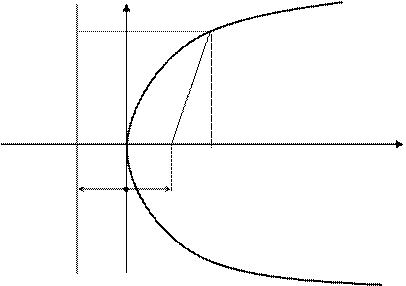
Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы y 2 = 2 px.
у
А r 1
М (х, у)
r 2
О F x
p /2
p /2
Величина р – расстояние от фокуса до директрисы – называется параметром параболы.
FM – фокальный радиус точки М
F (p /2, 0).
По определению: r 1 = r 2 .
Уравнение директрисы: 
.
Уравнения 
, 
, также определяют параболы.
Пример. На параболе у 2 = 8 х найти точку, расстояние от которой до директрисы равно 4.
Из уравнения параболы получаем, что р = 4.
r = x + p /2 = 4;
Следовательно
x = 2; y 2 = 16; y = ±4.
Искомые точки: M 1(2; 4), M 2(2; –4).
ОБЩЕЕ УРАВНЕНИЕ ЛИНИЙ ВТОРОГО ПОРЯДКА
Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям.
Уравнение эллипса с центром в точке 
и полуосями 
и 
.
.
Уравнение гиперболы с центром в точке и полуосями и .
.
Уравнения параболы с центром в точке .
Уравнение 
.
Теорема.
Уравнение всегда определяет: либо окружность (при 
), либо эллипс (при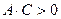 
), либо гиперболу (при 
), либо параболу (при 
).
При этом возможны случаи вырождения: для эллипса (окружности) – в точку или мнимый эллипс (окружность), для гиперболы – в пару пересекающихся прямых, для параболы – в пару параллельных прямых.
Контрольные вопросы:
1. Что такое эксцентриситет? Что он показывает?
2. Начертите, где находятся фокусы у эллипса и у гиперболы?
3. Можно ли записать уравнение гиперболы, зная только координаты ее правого фокуса?