Смешанное произведение векторов и его свойства.
Смешанное произведение в ортонормированном базисе.
3.Условия перпендикулярности, коллинеарности и компланарности векторов.
Примеры.
Аналитическая геометрия
Основные задачи аналитической геометрии
Полярная система координат
Опр. Смешанным (или векторно-скалярным) произведением векторов 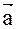 ,
, 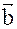 ,
, 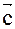 называется число (
называется число (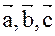 )=([
)=([ 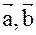 ],
], 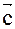 )
)
Теорема: (геометрический смысл смешанного произведения). Смешанное произведение векторов 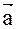 ,
, 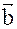 ,
, 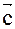 равно объему параллелепипеда построенного на этих векторах и взятому со знаком (+) если тройка правая и (–) если тройка левая.
равно объему параллелепипеда построенного на этих векторах и взятому со знаком (+) если тройка правая и (–) если тройка левая.
Построим параллелепипед, ребрами которого являются вектора 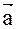 ,
, 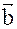 ,
, 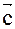 .
.
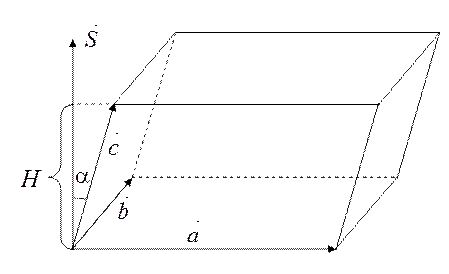 |
Найдем объем параллелепипеда 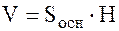 , где Sосн=Sпараллелограмма=
, где Sосн=Sпараллелограмма= 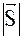 , где
, где 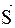 =
= 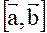 ;
; 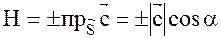
Где знак (+) соответствует острому углу a, в этом случае тройка векторов будет правой, знак (–) соответствует тупому углу a, или левой тройке векторов. На основании определения смешанного произведения имеем (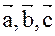 )=([
)=([ 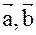 ],
], 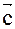 )=(
)=(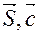 )=
)= 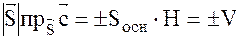 .
.
Свойства:
1)Смешанное произведение не меняется при циклической перестановке.
(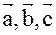 )=(
)=(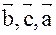 )=(
)=(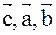 )=(
)=(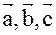 )
)
Так как в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2)При перестановке двух соседних сомножителей изменяется знак смешанного произведения.
(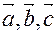 )=-(
)=-(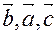 )
)
При перестановке объем сохраняется, но изменяется тройка векторов.
3)(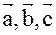 )=0, если векторы компланарны
)=0, если векторы компланарны
Смешанное произведение в ортонормированном базисе.
Пусть заданы векторы:
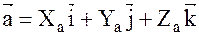 ;
; 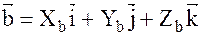 ;
; 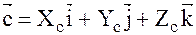 ;
;
Из условия задачи следует, что векторы заданы в ортонормированном базисе. Найдем смешанное произведение векторов: (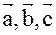 )=([
)=([ 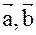 ],
], 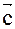 )=(
)=(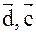 ), где
), где 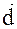 =[
=[ 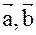 ]. Найдем вектор
]. Найдем вектор 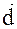 .
.
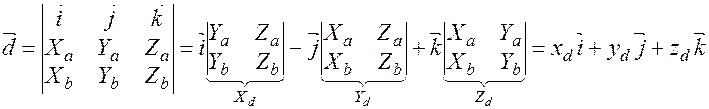
(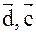 )=
)= 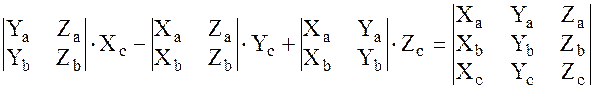 ;
;
(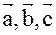 )=
)= 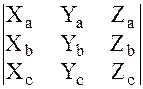 (1)
(1)
Это формула для смешанного произведения векторов в ортонормированном базисе.
3. Условия перпендикулярности, коллинеарности, и компланарности векторов.
1)Условие перпендикулярности.
(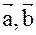 )
) 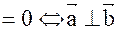 ;
;
(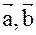 )=
)= 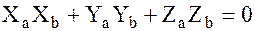 (2)
(2)
2.Условие коллинеарности.
[ 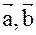 ]
] 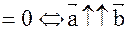 или
или 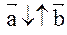
[ 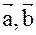 ]
] 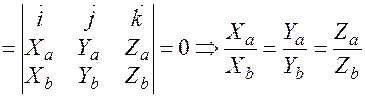
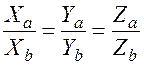 (3)
(3)
3.Условие компланарности.
(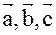 )
) 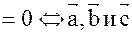 – компланарны.
– компланарны.
(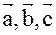 )
) 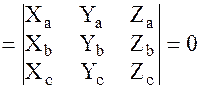 (4)
(4)
4. Примеры:
Пример 1. Найти объем и высоту треугольной пирамиды если заданы вершины.
А=(1; 0; 0); В=(-2; 1; 1); С=(-1; 1; 2); D=(0; 1; 4).
|
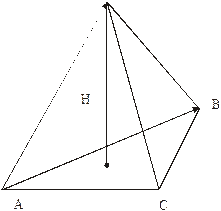
Решение: Введем векторы 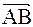 ={-3; 1; 1};
={-3; 1; 1}; 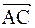 ={-2; 1; 2};
={-2; 1; 2};
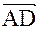 ={-1; 1; 4}. Из условия задачи следует, что базис ортонормированный.
={-1; 1; 4}. Из условия задачи следует, что базис ортонормированный.
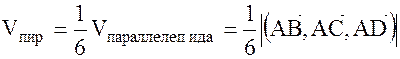 .
.
Применим формулу (1).
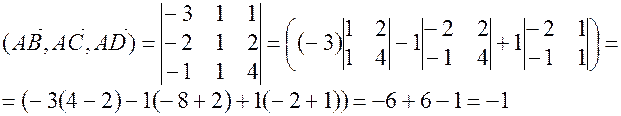
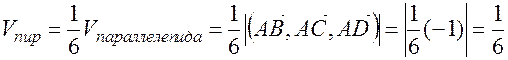
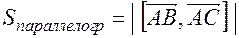
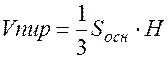 ; где
; где 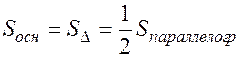 ;
;
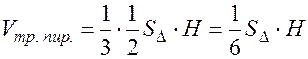
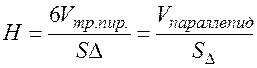 ;
;
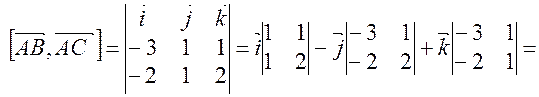
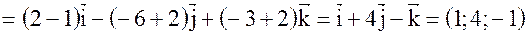
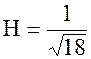
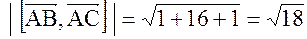 ;
; 
Задача 2. Выяснить компланарны ли векторы. Если нет, то как они ориентированы в пространстве?
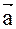 =(1; -2; 0);
=(1; -2; 0); 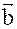 =(-1; 2; 2);
=(-1; 2; 2); 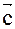 =(3; 0; -1)
=(3; 0; -1)
(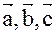 )
) 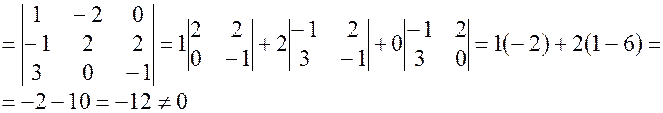 ;
;
т.к. (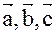 )<0, то они образуют левую тройку.
)<0, то они образуют левую тройку.
3.Найти площадь параллелограмма построенного на векторах: 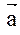 и
и 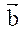 , если
, если 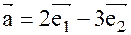 и
и 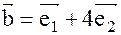 , где
, где 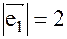 ;
; 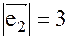 ; (
; (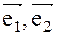 )
) 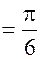
Решение: векторы 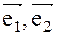 образуют не ортонормированный базис.
образуют не ортонормированный базис.
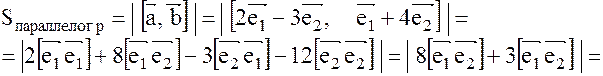
Аналитическая геометрия
Основные задачи аналитической геометрии
Задача 1. Пусть задано некоторое геометрическое место точек на плоскости или в пространстве, т.е. задана совокупность точек обладающих общимсвойством. Требуется получить уравнение этого геометрического места точек (уравнение прямой, плоскости, поверхности.)
Опр. Равенство F(x,y)=0 называется уравнением некоторой линии на плоскости, если координаты любой точки М(x,y) взятой на этой линий удовлетворяют данному уравнению. Пример: Прямая на плоскости, гипербола, окружность, парабола, эллипс.
Опр. Равенство F(x,y,z)=0 называется уравнением поверхности, если координаты любой точки М(x,y,z) взятой на этой поверхности удовлетворяют данному уравнению. Пример: плоскость, сфера, цилиндр, конус.
Задача 2. Обратная задаче 1. По заданному уравнению некоторого геометрического места точек, надо выяснить каким свойством обладают точки этого геометрического места точек.
Основной метод решения задач аналитической геометрии - метод координат. С декартовой системой координат мы знакомы, рассмотрим полярную систему координат.