Расчётно-графическая работа
По дисциплине «Общая электротехника»
Вариант № 20
Выполнил: ст. гр. ЭВС-23(оу)
Чиванов Э.А.
Проверил: ассистент каф.
РТиМБС
Тюкаев А.Ю.
Йошкар-Ола
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
Задание на расчётно-графическую работу
Введение 5
1. Расчёт электрической цепи постоянного тока 6
2. Расчёт электрической цепи переменного тока 15
Заключение 28
Приложение А
Приложение Б
Приложение В
Приложение Г
ЗАДАНИЕ НА РАСЧЁТНО-ГРАФИЧЕСКУЮ РАБОТУ
1. Расчёт электрической цепи постоянного тока.
1.1. Начертите принципиальную схему цепи (рис.1), заданной таблицей 1 и номером варианта.
Параметры элементов схемы указаны в таблице 1.
 |
Рис.1.
Таблица 1 – Параметры элементов электрической цепи
| Параметры элементов электрической цепи | |||||||||||||
| R1, кОм | R2, кОм | R3, кОм | R4, кОм | R5, кОм | R6, кОм | Параметры источников электрической энергии | |||||||
| E1, В | E2, В | E3, В | E4, В | r1, Ом | r2, Ом | r3, Ом | r4, Ом | ||||||
| 0,01 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,9 | 0,8 | 0,7 |
1.2. Постройте граф исследуемой электрической цепи, используя сокращённое и расширенное топологические описания.
1.3. Рассчитайте токи и напряжения ветвей методом контурных токов.
1.4. Рассчитайте токи и напряжения ветвей методом узловых потенциалов.
1.5.Определите мощность потерь и коэффициент полезного действия электрической цепи (сопротивлением проводов пренебречь).
2. Расчёт электрической цепи переменного тока.
2.1. Начертите принципиальную схему цепи (рис.2), заданной таблицей 2 и номером варианта.
Параметры элементов схемы и вид двухполюсников указаны в таблице 2.
2.2. Рассчитайте сопротивление всех ветвей и запишите в показательной и алгебраической формах. Определите активное и реактивное сопротивление каждой ветви.
Таблица 2 – Параметры элементов электрической цепи
| Параметры элементов электрической цепи | ||||||||||||||||||||
| R1, кОм | R2, кОм | R3, кОм | C1, нФ | C2, нФ | C3, нФ | L1, мкГн | L2, мкГн | Параметры источников электрической энергии | Вид двухполюсника | |||||||||||
| E1,В | f1, кГц | φ1, рад | r1, Ом | E2,В | f2, кГц | φ2, рад | r2, Ом | D1 | D2 | |||||||||||
| CD1, нФ | LD1, мкГн | CD2, нФ | LD2, мкГн | |||||||||||||||||
| 0,5 | 0,6 | 0,5 | 
| 1,5 | 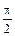
| 2,0 | - | - |

Рис.2.
2.3. Запишите основную систему уравнений электрического равновесия для мгновенных значений токов и напряжений.
2.4. Используя символический метод расчёта электрических цепей, найдите токи и напряжения всех ветвей. Определите активную и реактивную составляющие тока и напряжения каждой ветви.
2.5. Для каждой ветви электрической цепи постройте полную векторную диаграмму токов и напряжений.
2.6. Для ветвей электрической цепи с источниками напряжения  и
и  найдите комплексную, полную, активную и реактивную мощности.
найдите комплексную, полную, активную и реактивную мощности.
2.7. Постройте графики мгновенных значений токов, напряжений, мощностей в ветвях с источниками напряжения  и
и  .
.
 Введение
Введение
Данная расчётно-графическая работа посвящена изучению теории линейных электрических цепей. Теория линейных электрических цепей является основной теоретической базой в подготовке инженеров по радиотехнике, радиосвязи, радиовещанию, телевидению и другим специальностям. Данная расчётно-графическая работа поможет усвоению основных методов расчета электрических цепей переменного и постоянного тока, также усвоению расчетов основных характеристик любой цепи: силы тока, напряжения, сопротивления, мощности, коэффициента полезного действия.
1.  Расчёт электрической цепи постоянного тока
Расчёт электрической цепи постоянного тока
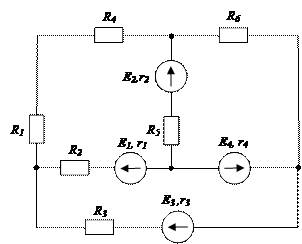
1.1. В соответствии с вариантом задания начертим принципиальную схему электрической цепи (рис.3,а). Параметры элементов схемы указаны в таблице 1.
 |
а)
 | |||
 | |||
б) в)
Рис.3.
1.2. Построим граф исследуемой электрической цепи, используя сокращённое и расширенное топологические описания.
На рис.3,б-в представлены графы схемы электрической цепи (рис.3,а) с сокращённым и топологическим описаниями соответственно.
 1.3. Рассчитаем токи и напряжения ветвей схемы электрической цепи (рис.4) методом контурных токов. Для этого, предположим, что в каждом контуре протекает свой контурный ток:
1.3. Рассчитаем токи и напряжения ветвей схемы электрической цепи (рис.4) методом контурных токов. Для этого, предположим, что в каждом контуре протекает свой контурный ток:  ,
,  ,
,  (рис.4).
(рис.4).
 |
Рис.4
Составим уравнения по второму закону Кирхгофа для контурных токов, с учётом внутреннего сопротивления источников напряжения.
Для первого контура:
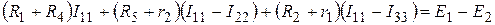 . (1)
. (1)
Для второго контура:
 . (2)
. (2)
Для третьего контура:
 . (3)
. (3)
В уравнениях (1) – (2) раскроем скобки и сгруппируем слагаемые по  ,
,  ,
,  . В результате получим систему уравнений (4).
. В результате получим систему уравнений (4).
 (4)
(4)
Решим данную систему уравнений матричным методом. Для этого произведём в (4) следующую замену:
 ;
;  ;
;  ;
;

 ;
; 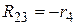 ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
В результате получим:
 , (5)
, (5)
или в матричном виде:
 , (6)
, (6)
где
 ;
;  ;
;  (7)
(7)
Учитывая данные таблицы 1, получим:
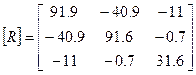 ;
; 
Рассчитаем токи  ,
,  ,
,  в среде MathCad (см. приложение А). Получим следующие значения контурных токов:
в среде MathCad (см. приложение А). Получим следующие значения контурных токов:

 А;
А;  А;
А;  А.
А.
Найдём токи в ветвях электрической цепи (рис.4).
 ;
;  ;
;  ;
;
(8)
 ;
;  ;
; 
Таким образом:
 А;
А;  А;
А;
 А;
А;  А;
А;
 А;
А;  А.
А.
На рис.5 указаны положительные направления токов  ,
,  ,
,  ,
,  ,
,  ,
,  , значения которых равны соответственно
, значения которых равны соответственно  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 |
Рис.5
Найдём напряжения ветвей схемы электрической цепи (рис.5) по обобщённому закону Ома:


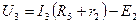
(9)



 Таким образом, напряжения ветвей равны:
Таким образом, напряжения ветвей равны:
 В;
В;
 В;
В;
 В;
В;
 В;
В;
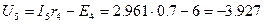 В;
В;
 В.
В.
На рис.5 указаны положительные направления напряжений ветвей  ,
,  ,
,  ,
,  ,
,  ,
,  , значения которых равны
, значения которых равны  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 1.4. Рассчитаем токи и напряжения ветвей схемы электрической цепи (рис.6) методом узловых потенциалов.
1.4. Рассчитаем токи и напряжения ветвей схемы электрической цепи (рис.6) методом узловых потенциалов.
Рис.6.
Для этого найдём потенциалы узлов схемы (рис.6). Примем потенциал узла 0 равным нулю и найдём потенциалы всех оставшихся узлов. Согласно методу узловых потенциалов, составим следующую систему уравнений:
 , (10)
, (10)
 где
где 

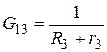

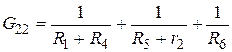





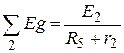

Запишем систему уравнений (10) в матричном виде:
 , (11)
, (11)
где

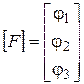

Решим уравнение (11), используя среду MathCad (см.приложение Б). Получим следующие значения узловых потенциалов:
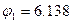 В;
В;  В;
В;  В (12)
В (12)
Найдём напряжения ветвей электрической схемы:
 В;
В;
 В;
В;
 В;
В;

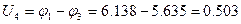 В;
В;
 В;
В;
 В.
В.
Используя обобщённый закон Ома для участка цепи, рассчитаем токи ветвей:
 А;
А;
 А;
А;
 А;
А;
 А;
А;
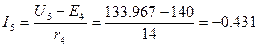 А;
А;
 А.
А.
 |
Рис.7.
На рис.7 показаны положительные направления токов и напряжений ветвей.
1.5. Определим мощность потерь и коэффициент полезного действия электрической цепи (рис.7), пренебрегая сопротивлением проводов.
Будем считать полезной нагрузкой все сопротивления электрической цепи, кроме внутренних сопротивлений источников электрической энергии. Также учтём следующее: если направление тока ветви совпадает с направлением источника ЭДС ветви, то источник вырабатывает электрическую энергию. Если же направление тока противоположно направлению ЭДС, то источник работает в режиме потребителя и является приёмником электрической энергии. Мощность, которую потребляет источник энергии, будем считать полезной. Тогда полезная мощность будет равна:
 , (13)
, (13)
откуда

 Мощность потерь будет равна мощности, которая выделяется на внутренних сопротивлениях источников энергии:
Мощность потерь будет равна мощности, которая выделяется на внутренних сопротивлениях источников энергии:
 , (14)
, (14)
откуда
 .
.
Полная мощность цепи равна мощности, которую отдают источники электрической энергии в цепь:
 , (15)
, (15)
откуда
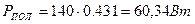
 Найдём коэффициент полезного действия цепи:
Найдём коэффициент полезного действия цепи:

2. Расчёт электрической цепи переменного тока.
 2.1. В соответствии с вариантом задания начертим принципиальную схему электрической цепи, также произвольно зададим направления токов ветвей (рис.8). Параметры элементов схемы и вид двухполюсников указаны в таблице 2.
2.1. В соответствии с вариантом задания начертим принципиальную схему электрической цепи, также произвольно зададим направления токов ветвей (рис.8). Параметры элементов схемы и вид двухполюсников указаны в таблице 2.
Рис.8.
2.2. Рассчитаем сопротивление всех ветвей электрической цепи (рис.8) и запишем в показательной и алгебраической формах.
Комплексное сопротивление ветвей, с учётом внутреннего сопротивления источников электрической энергии:
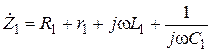


 (16)
(16)

 ,
,
где  Гц.
Гц.
 Запишем сопротивления ветвей в алгебраической форме:
Запишем сопротивления ветвей в алгебраической форме:
 Ом;
Ом;
 Ом;
Ом;
 Ом; (17)
Ом; (17)
 Ом;
Ом;
 Ом,
Ом,
Учитывая данные таблицы 2, получим:
 Ом;
Ом;
 Ом;
Ом;
 Ом;
Ом;  Ом; (18)
Ом; (18)
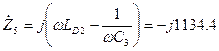 Ом,
Ом,
Запишем сопротивления ветвей в показательной форме. В общем случае комплексное сопротивление ветви в показательной форме имеет вид:
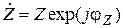 , (19)
, (19)
где
 (20)
(20)
 , при
, при  ;
;  , при
, при 
 Используя формулы (20), запишем комплексное сопротивление ветвей в показательной форме:
Используя формулы (20), запишем комплексное сопротивление ветвей в показательной форме:
 Ом;
Ом;
 Ом;
Ом;
 Ом; (21)
Ом; (21)
 Ом;
Ом;
 Ом.
Ом.
Определим активное и реактивное сопротивление каждой ветви:
для первой ветви:  Ом;
Ом;  Ом;
Ом;
для второй ветви: 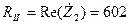 Ом;
Ом;  Ом;
Ом;
для третей ветви:  Ом;
Ом; 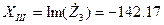 Ом;
Ом;
для четвёртой ветви:  Ом;
Ом;  Ом;
Ом;
для пятой ветви:  Ом;
Ом;  Ом;
Ом;
Запишем основную систему уравнений электрического равновесия цепи (рис.8) для мгновенных значений токов и напряжений.
Топологические уравнения ветвей:
по первому закону Кирхгофа для мгновенных значений:
 ;
; 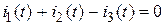 ;
;
 .
.
По второму закону Кирхгофа для мгновенных значений:
 ;
;
 ;
;
 ,
,
где  В;
В;  В.
В.
 Компонентные уравнения ветвей:
Компонентные уравнения ветвей:
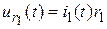 ;
;  ;
;  ;
; 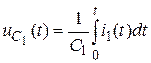 ;
;
 ;
;  ;
; 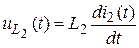 ;
;  ;
;
 ;
;
 ;
;  ;
;  ;
;
 ;
;  .
.
Компонентные и топологические уравнения ветвей составляют основную систему уравнений электрического равновесия цепи.
Используя символический метод расчёта электрических цепей, найдём токи и напряжения всех ветвей электрической цепи (рис.9).
 |
Рис.9.
Предположим, что в каждом контуре протекает свой контурный ток, комплексные амплитуды которых равны соответственно:  (рис.9).
(рис.9).
Запишем уравнения по второму закону Кирхгофа для токов  .
.  В результате получим следующую систему уравнений:
В результате получим следующую систему уравнений:
 , (20)
, (20)
где  комплексные сопротивления ветвей исследуемой электрической цепи (см. формулы 18);
комплексные сопротивления ветвей исследуемой электрической цепи (см. формулы 18);  и
и 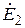 комплексные амплитуды источников электрической энергии:
комплексные амплитуды источников электрической энергии:
 ,
,  . (21)
. (21)
Подставляя (18) и (21) в систему уравнений (20), получим матричное уравнение:
 (22)
(22)
где
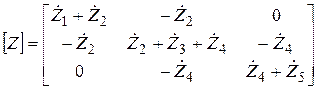 ;
;  ;
; 
Решая матричное уравнение (22) в среде MathCad (см. приложение В), получим следующие значения контурных токов:
 А;
А;
 А; (23)
А; (23)
 А.
А.
 Найдём комплексные амплитуды токов ветвей электрической цепи (рис.9):
Найдём комплексные амплитуды токов ветвей электрической цепи (рис.9):
 А;
А;
 А;
А;
 А; (24)
А; (24)
 ;
;
 А.
А.
Используя (24) определим активную и реактивную составляющие токов ветвей:
для первой ветви:  А;
А;  А;
А;
для второй ветви:  А;
А;  А;
А;
для третей ветви:  А;
А;  А;
А;
для четвёртой ветви:  А;
А;  А;
А;
для пятой ветви:  А;
А;  А;
А;
Используя формулы перехода комплексных амплитуд к мгновенным значениям тока и учитывая, что циклическая частота  , получим мгновенные значения токов ветвей:
, получим мгновенные значения токов ветвей:
 А;
А;
 А;
А;
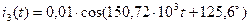 А; (25)
А; (25)
 А;
А;
 А.
А.
 Применяя обобщённый закон Ома для комплексных величин, найдём комплексные амплитуды напряжений ветвей:
Применяя обобщённый закон Ома для комплексных величин, найдём комплексные амплитуды напряжений ветвей:
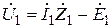 ;
;
 ;
;
 ; (26)
; (26)
 ;
;
 .
.
Подставляя (18), (21) и (24) в (26), получим:
 ;
;
 ;
;
 ; (27)
; (27)
 ;
;
 .
.
Вычисляя значения выражений (27), получим комплексные амплитуды напряжений ветвей:
 В;
В;
 В;
В;
 В; (28)
В; (28)
 В;
В;
 В.
В.
Определим активную и реактивную составляющие напряжений ветвей:
для первой ветви:  В;
В; 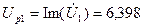 В;
В;
для второй ветви:  В;
В;  В;
В;
для третей ветви:  В;
В;  В;
В;
для четвёртой ветви:  В;
В;  В;
В;
для пятой ветви:  В;
В;  В;
В;
Используя формулы перехода комплексных амплитуд к мгновенным значениям напряжения и учитывая, что циклическая частота  , получим мгновенные значения напряжений ветвей:
, получим мгновенные значения напряжений ветвей:
 В;
В;
 В;
В;
 В; (29)
В; (29)
 В;
В;
 В.
В.
 2.5.Для каждой ветви электрической цепи построим полную векторную диаграмму токов и напряжений. Для этого воспользуемся данными, полученными в пункте 2.4. На рис.10 представлены диаграммы токов и напряжений ветвей электрической цепи (рис.9). Для улучшения наглядности модули векторов
2.5.Для каждой ветви электрической цепи построим полную векторную диаграмму токов и напряжений. Для этого воспользуемся данными, полученными в пункте 2.4. На рис.10 представлены диаграммы токов и напряжений ветвей электрической цепи (рис.9). Для улучшения наглядности модули векторов  ,
,  ,
,  ,
,  ,
,  показаны в масштабе 1:1; модули векторов
показаны в масштабе 1:1; модули векторов 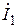 ,
,  ,
,  ,
, 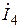 ,
,  увеличены в 1000 раз.
увеличены в 1000 раз.

| |||||||||||||||||||

| |||||||||||||||||||
 Рис.10.
Рис.10.
2.6 Для ветвей электрической цепи с источниками ЭДС  и
и  найдём комплексную, полную, активную и реактивную мощности.
найдём комплексную, полную, активную и реактивную мощности.
Найдём напряжения и токи в ветвях с источниками ЭДС  и
и  в показательной форме. Так как:
в показательной форме. Так как:
 В
В
 В;
В;
 А;
А;
 А;
А;
то, пользуясь формулами (20), получим:
 В;
В;  ;
;
 В;
В; 
 А;
А;  ;
;
 А;
А;  ,
,
 поэтому
поэтому
 В;
В;
 В;
В;
 А;
А;
 А.
А.
Комплексная мощность равна:
 , (30)
, (30)
где  - комплексно-сопряжённое значение тока
- комплексно-сопряжённое значение тока  . Так как
. Так как 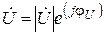 и
и  , то комплексную мощность можно записать в следующем виде:
, то комплексную мощность можно записать в следующем виде:
 (31)
(31)
Модуль комплексной мощности есть полная мощность:
 (32)
(32)
Мощность, выделяющаяся на активных элементах:
 (33)
(33)
Мощность реактивных элементов:
 (34)
(34)
Пользуясь формулами (30)-(34), найдём комплексную, полную, активную и реактивную мощности в ветвях с источниками ЭДС  и
и  . В результате получим:
. В результате получим:
Для первой ветви:
комплексная мощность:

полная мощность:


 ;
;
активная мощность:
 Вт;
Вт;
реактивная мощность.
 Вар;
Вар;
Для второй ветви:
комплексная мощность:

полная мощность:
