Определение средней и предельной ошибки выборки.

Существует показатель «средняя ошибка выборки». В случае случайного и механического отбора средняя ошибка выборки: для повторного отбора - n-число выборки; N- число ген. совокуп.; δ-дисперс.признака ген.совокуп.

Предельная ошибка выборки. Представляет t кратную срен. ошибку. 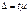t-коэф.доверия, которя определяется по таблице знач. интегральной функции Лапласа, при заданной вер-ти. Наиболее употребляемые значения доверительной вре-ти и соответствующие им значения t приведены в табл.

Зная выборочную среднюю и предельную ошибку можно определить пределы в которых находиться значение средней ген. совокупности. - доверительный интервал для средн.ген. совокупности.

Определение величины доверительных интервалов при расчете обобщающих показателей генеральной совокупности.

Прежде всего выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней, которая показывает (с определенной вероятностью) на сколько выборочная средняя может отличаться от генеральной средней в большую и меньшую стороны.

Тогда величина искомой генеральной средней находится в доверительном интервале:

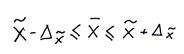, где х – среднее значение признака выборочной совокупности, ∆ _x – предельная ошибка средней

х – генеральная средняя (среднее значение признака в генеральной совокупности)

Аналогичным образом для доли величина генеральной доли находится в доверительном интервале: w-∆ _р ≤ р ≤ w+∆ _р w – выборочна доля (доля единиц) ∆ _р – предельная ошибка доли р - генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности).

Корреляционный анализ: проверка коэффициента корреляции и коэффициента регрессии на достоверность. Критерий Стъюдента.

Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.

Проверка на значимость:

1)при заданном уровне 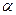выдвигается гипотеза Н0, состоящая в том что коэф-т корр-ии =0

2)в качестве критерия проверки выдвигается случайная величина 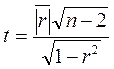-оценка коэф.корр-ии.

3)в предположении справедливости Н0, tдолжно быть распределено по tкритерию Стьюдента =n-2 (число степеней свободы). Рассчитываем наблюдаемые значения критерий.

4)по табл.критич.точ. t- Стьюдента находим сравниваем если 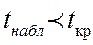то Н0 принимается, что означает коэ-т кор-ии =0, т.е r=0 если 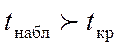то Н0 отвергается, значит наша оценка значима.

-критерий Стьюдента - общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.