В случае большой выборки (n³100) предельную ошибку для среднего выборки можно рассчитать в Excel при помощи функции
ДОВЕРИТ(альфа; станд.откл; размер),
альфа — допустимая вероятность ошибки, т.н. уровень значимости: альфа = 1-b;
станд.откл. — генеральное среднее квадратическое отклонение, предполагающееся известным, или его оценка  ;
;
размер — текущий объем выборки n.
При помощи формулы предельной ошибки выборки определяют доверительный интервал с заданной доверительной вероятностью g для генерального среднего  :
:  . При этом
. При этом  .
.
В случае малой выборки (n<30) при отсутствии данных о нормальности распределения признака предельная ошибка для генеральной средней определяется по формуле: 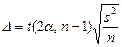 , где
, где
 — табличное значение критерия Стьюдента для вероятности 2a=1-b при числе степеней свободы
— табличное значение критерия Стьюдента для вероятности 2a=1-b при числе степеней свободы  . В Excel коэффициент доверия для малой выборки рассчитывается при помощи функции =СТЬЮДРАСПОБР(вероятность; степени свободы), где за аргумент вероятность принимается уровень значимости 2a=1-b.
. В Excel коэффициент доверия для малой выборки рассчитывается при помощи функции =СТЬЮДРАСПОБР(вероятность; степени свободы), где за аргумент вероятность принимается уровень значимости 2a=1-b.
Для 30<n<100 причисление выборки к категории «большой» или «малой» индивидуально, зависит от постановки задачи и от дисперсии выборки. Четкой границы между большой и малой выборками в общем случае указать невозможно. Выборка, сделанная из совокупности с небольшим разбросом признака, может считаться большой, тогда как выборка такого же объема, произведенная из более разнородной совокупности, окажется малой.
Пример 2.1.
Имеются данные по уровню безработицы в России в 2006 году:
| Центральный фед.окр. | Калининградская обл. | 4,5 | Респ.Мордовия | 4,7 | Респ.Хакасия | 9,1 | |
| Белгородская обл. | 4,1 | Ленинградская обл. | 5,9 | Респ.Татарстан | 5,6 | Алтайский край | 8,8 |
| Брянская обл. | 5,6 | Мурманская обл. | 6,7 | Удмуртская респ. | 8,4 | Красноярский край | 9,9 |
| Владимирская обл. | 6,8 | Новгородская обл. | 5,5 | Чувашская респ. | 8,6 | Таймырский АО | 10,0 |
| Воронежская обл. | 10,9 | Псковская обл. | 7,4 | Пермский край | 6,9 | Эвенкийский АО | 3,9 |
| Ивановская обл. | 5,5 | Г.Санкт-Петербург | 2,4 | Кировская обл. | 7,9 | Иркутская обл | 8,9 |
| Калужская обл | 4,2 | Южный фед. Округ | Нижегородская обл. | 5,3 | Усть-Ордынский АО | 12,6 | |
| Костромская обл. | 5,6 | Респ.Адыгея | 13,7 | Оренбургская обл. | 6,5 | Кемеровская обл. | 7,3 |
| Курская обл. | 5,0 | Респ.Дагестан | 22,3 | Пензенская обл. | 6,5 | Новосибирская обл. | 7,4 |
| Липецкая обл. | 7,3 | Респ.Ингушетия | 58,5 | Самарская обл. | 4,3 | Томская обл. | 9,3 |
| Московская обл. | 4,9 | Кабардино-балк.респ. | 20,7 | Саратовская обл. | 8,2 | Читинская обл. | |
| Орловскся обл. | 3,0 | Респ.Калмыкия | 16,7 | Ульяновская обл. | 6,9 | Агинский АО | 0,9 |
| Рязанская облюю | 6,0 | Карачаево-Черк.респ. | 19,4 | Уральский фед. округ | Дальневост. фед.округ | ||
| Смоленская обл. | 5,2 | Респ.Сев.Осетия | 8,5 | Курганская обл. | 12,4 | Респ.Саха | 9,5 |
| Тамбовская обл. | 8,0 | Чеченская респ. | 66,9 | Свердловская обл. | 7,0 | Приморский край | 8,0 |
| Тверская обл. | 8,7 | Краснодарский край | 7,4 | Тюменская обл. | 6,8 | Хабаровский край | 6,0 |
| Тульская обл. | 4,5 | Ставроп. Край | 8,9 | Ханты-Манс. АО | 6,1 | Амурская обл. | 8,2 |
| Ярославская обл. | 2,7 | Архангельская обл. | 7,9 | Ямало-НенецкийАО | 5,4 | Камчатская обл. | 9,1 |
| Г.Москва | 3,0 | Волгоградская обл. | 8,6 | Челябинская обл. | 5,1 | Корякский АО | 6,4 |
| Северо-зап. фед. округ | Ростовская обл. | 8,0 | Сибирский фед. окр | Магаданская обл. | 5,4 | ||
| Респ. Карелия | 3,6 | Приволжский фед. окр | Респ. Алтай | 11,6 | Сахалинская обл. | 4,6 | |
| Респ. Коми | 12,4 | Респ.Башкортостан | 6,5 | Респ. Бурятия | 13,4 | Еврейская АО | 9,8 |
| Архангельская обл. | 5,9 | Респ.Марий Эл | 10,2 | Респ. Тыва | 20,5 | Чукотский АО | 3,7 |
| Вологодская обл. | 5,6 |
Определить доверительный интервал с надежностью 0,9 для средней безработицы: 1) считая выборку большой; 2) считая выборку малой.
Решение. Откроем таблицы Excel. Внесем выборочные данные по всем округам в столбец А (диапазон А2:А87). В ячейках D2:D5 вычислим характеристики выборки: объем выборки n (функция СЧЁТ), среднее значение х ср (функция СРЗНАЧ), выборочную дисперсию s2 (функция ДИСПР), исправленную дисперсию s2испр (функция ДИСП). Внесем значение доверительной вероятности Р=0,9.
Поскольку выборка считается большой, мы должны использовать формулу стандартной ошибки для среднего большой выборки. Однако в этом случае проще сразу вычислить предельную ошибку при помощи функции ДОВЕРИТ:
Рисунок 2.1. Пример. Расчет предельной ошибки среднего большой выборки

Получили D=1,63835. Тогда доверительный интервал для среднего уровня безработицы 9,08±1,64.
1) Применим теперь формулу ошибки для малой выборки. Вычислим коэффициент доверия t, введя в ячейку G8 формулу =СТЬЮДРАСПОБР(1-D6;D2-1). Предельную ошибку вычислим в ячейке G9:

Получили D=1,656403. Тогда доверительный интервал для среднего уровня безработицы 9,08±1,656.
Видим, что предельная ошибка, вычисленная по формуле для малой выборки несколько больше, чем по формуле для большой выборки, но различие в данном случае невелико. С ростом объема выборки это различие уменьшается.
Доверительный интервал для дисперсии s2 вычисляется по формуле
(n-1)*s2 / c2(a; n-1) < s2 < (n-1)*s2 / c2(1-a; n-1), (*)
где значение c2(a; n-1) находится с помощью функции функция =ХИ2ОБР(a; n-1) при уровне значимости a и n-1 степени свободы. Для нахождения доверительного интервала для среднего квадратического отклонения s извлекаются корни квадратные из концов интервала (*).
Критерий Фишера
В Excel критическое значение критерия Фишера можно рассчитать при помощи функции FРАСПОБР(вероятность;степени_свободы1;степени_свободы2), где вероятность – уровень значимости a=(1-β)/2.
Для определения уровня вероятности выполнения гипотезы о равенстве дисперсий может быть использована функция ФТЕСТ(массив1;массив2), которая возвращает одностороннюю (для простой альтернативной гипотезы) вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно.
| СУММ | Суммирует аргументы. |
| СУММПРОИЗВ | Вычисляет сумму произведений соответствующих элементов массивов. |
| СУММКВ | Вычисляет сумму квадратов аргументов. |
| СУММРАЗНКВ | Вычисляет сумму разностей квадратов соответствующих значений в двух массивах. |
| СУММСУММКВ | Вычисляет сумму сумм квадратов соответствующих элементов двух массивов. |
| СУММКВРАЗН | Вычисляет сумму квадратов разностей соответствующих значений в двух массивах. |
| СРЗНАЧ | Вычисляет среднее арифметическое аргументов. |
| ХИ2ОБР | Вычисляет обратное значение односторонней вероятности распределения хи-квадрат. |
| ДОВЕРИТ | Определяет доверительный интервал для среднего значения по генеральной совокупности. |
| КОРРЕЛ | Находит коэффициент корреляции между двумя множествами данных. |
| СЧЁТ | Подсчитывает количество чисел в списке аргументов. |
| FРАСПОБР | Определяет обратное значение для F-распределения вероятности. |
| ФТЕСТ | Определяет результат F-теста. |
| ЭКСЦЕСС | Определяет эксцесс множества данных. |
| МАКС | Определяет максимальное значение из списка аргументов. |
| МЕДИАНА | Находит медиану заданных чисел. |
| МИН | Определяет минимальное значение из списка аргументов. |
| МОДА | Определяет значение моды множества данных. |
| НОРМРАСП | Выдает нормальную функцию распределения. |
| НОРМОБР | Выдает обратное нормальное распределение. |
| НОРМСТРАСП | Выдает стандартное нормальное интегральное распределение. |
| НОРМСТОБР | Выдает обратное значение стандартного нормального распределения. |
| ПИРСОН | Определяет коэффициент корреляции Пирсона. |
| СКОС | Определяет асимметрию распределения. |
| СТАНДОТКЛОН | Оценивает стандартное отклонение по выборке. |
| СТАНДОТКЛОНП | Определяет стандартное отклонение по генеральной совокупности. |
| СТЬЮДРАСП | Выдает t-распределение Стьюдента. |
| СТЬЮДРАСПОБР | Выдает обратное t-распределение Стьюдента. |
| ТТЕСТ | Находит вероятность, соответствующую критерию Стьюдента. |
| ДИСП | Оценивает дисперсию по выборке. |
| ДИСПР | Вычисляет дисперсию для генеральной совокупности. |
| КОРЕНЬ | Вычисляет положительное значение квадратного корня. |
| ОКРУГЛ | Округляет число до указанного количества десятичных разрядов. |
| ПРОИЗВЕД | Вычисляет произведение аргументов. |
| СУММ | Суммирует аргументы. |
| СУММКВ | Вычисляет сумму квадратов аргументов. |
| СУММКВРАЗН | Вычисляет сумму квадратов разностей соответствующих значений в двух массивах. |
| СУММПРОИЗВ | Вычисляет сумму произведений соответствующих элементов массивов. |
| СУММРАЗНКВ | Вычисляет сумму разностей квадратов соответствующих значений в двух массивах. |
| СУММСУММКВ | Вычисляет сумму сумм квадратов соответствующих элементов двух массивов. |