Транспортная задача
На трех станциях отправления имеется соответственно 30, 50, и 20 ед. однородного груза, который нужно доставить в четыре пункта назначения согласно их потребностям. Эти данные, а также стоимость перевозки единицы груза от каждой станции отправления к каждому пункту назначения указаны в таблице. Составить план перевозок грузов, чтобы затраты на эти перевозки были минимальными.
| Пункты отправления | Запасы груза | Пункты назначения | |||

| 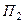
| 
| 
| ||

| |||||
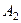
| |||||

| |||||
| Потребности |
Решение.
Этап 1.
Часто условие транспортной задачи оформляют матрицей:
Построим математическую модель транспортной задачи.
1. «Составить план перевозок грузов» - значит определить сколько, от куда и куда надо перевезти груза, чтобы достичь поставленной цели - «затраты на эти перевозки были минимальными». Введем управляющие переменные:  - количество груза, перевозимого из пункта
- количество груза, перевозимого из пункта  в пункт
в пункт  (
(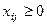 ).
).
2. Стоимость этой перевозки составит  . Тогда целевая функция - суммарные затраты, связанные с реализацией всего плана перевозок – запишется выражением:
. Тогда целевая функция - суммарные затраты, связанные с реализацией всего плана перевозок – запишется выражением:
в общем виде  , где
, где
в нашей задаче 
3. Для построения системы ограничений проверим, является ли задача сбалансированной.
Суммарная мощность поставщиков  ед
Суммарная мощность потребителей ед
Суммарная мощность потребителей 
| 
|
Следовательно, условие сбалансированности не выполнено.
4. Запишем систему ограничений:
По потребителю: мощности поставщиков меньше мощности потребителей, следовательно, кто-то из потребителей получит груза меньше, чем его потребность  .
.
Количество груза, которое потребитель  действительно получит запишется выражением:
действительно получит запишется выражением: 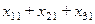 . Так как это меньше, чем его потребность, ограничение будет иметь вид:
. Так как это меньше, чем его потребность, ограничение будет иметь вид:  .
.
Аналогично строятся ограничения по другим потребителям. Так как в задаче заранее не оговаривается, потребности какого потребителя не будут удовлетворены, знак  поставим в ограничениях по всем потребителям. Получим систему ограничений по потребителю:
поставим в ограничениях по всем потребителям. Получим систему ограничений по потребителю:
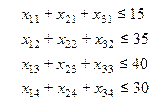
По поставщику: весь имеющийся на станции отправления груз будет вывезен (т.е. 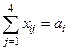 ):
):
 ;
;
Прямые ограничения 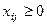 .
.
Этап 2.
1. Подготовим форму для ввода исходных данных (Рис 15.),
В нашем примере матрица затрат по доставке груза с конкретной станции отправления каждому потребителю  вводится в ячейки блока В3:E5. В ячейках В6:E6 указываются потребности
вводится в ячейки блока В3:E5. В ячейках В6:E6 указываются потребности  в пунктах назначения
в пунктах назначения  , мощности
, мощности  поставщиков
поставщиков  записаны в блоке F3:F5.
записаны в блоке F3:F5.

Рис. 15 Ввод исходных данных.
2. Зарезервируем изменяемые ячейки, в которых после решения задачи будет находиться оптимальный план перевозок  . Размерность этого массива обязательно должна совпадать с размерностью матрицы затрат: выделим блок ячеек I3:L5 (можно ввести в эти ячейки «1») (рис. 16).
. Размерность этого массива обязательно должна совпадать с размерностью матрицы затрат: выделим блок ячеек I3:L5 (можно ввести в эти ячейки «1») (рис. 16).

Рис 16. Создание формы для ввода условий задачи.
3. Введем зависимость для целевой функции (рис. 17). Оптимальное значение целевой функции будет помещено в ячейке В8:
· Курсор в ячейку В8  .
.
· Мастер функций fx / Математические / СУММПРОИЗВ (В3:E5; I3:L5)

Рис. 17 Ввод зависимости для целевой функции
4. Введем зависимости ограничений, стоящие в левых частях ограничений.
- вводим условия реализации мощностей поставщиков (рис 18.):
· Курсор в ячейку М3. 
· Мастер функций fx / Математические / СУММ (I3:L3)
· Курсор в ячейку М3.
· Растянуть (копировать) ячейку М3 в ячейки М4 и М5.

Рис. 18. Ввод зависимостей ограничений по поставщикам.
- вводим зависимостей ограничений по потребителям (рис. 19):
· курсор в ячейку I6.  ;
;
· Мастер функций fx / Математические / СУММ (I3:I5)
· Курсор в ячейку I6.
· Растянуть (копировать) ячейку I6 в ячейки J6, K6 и L6.

Рис. 19. Ввод зависимостей ограничений по потребителям.
На этом ввод зависимостей закончен.
Этап 3. Запуск программы Поиск решений
После выбора команд Поиск решения появится диалоговое окно Поиск решения.
· Назначение целевой ячейки: курсор в поле Установить целевую ячейку.  . Левой кнопкой мыши щелкнуть на ячейке В8.
. Левой кнопкой мыши щелкнуть на ячейке В8.
· Ввести направление целевой функции: минимальному значению.
· Ввести адреса искомых переменных: курсор в поле Изменяя ячейки.  . Выделить мышью адреса ячеек I3:L5.
. Выделить мышью адреса ячеек I3:L5.
· Ввести ограничения:
o курсор в поле Ограничения  . Выбрать режим Добавить
. Выбрать режим Добавить  .
.
o курсор в поле Ссылка на ячейку 
o выбрать мышью ячейки I6:L6
o ввести знак ограничения <=
o курсор в правое окно Ограничение  .
.
o указать мышью адреса В6:E6
o 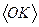
Остальные ограничения ввести аналогично. В результате этих действий окно Поиск решений будет выглядеть, как представлено на рис 20.

Рис. 20. Введены все ограничения.
· Выбрать параметры модели: рис 4.
Этап 4. Выполнить.
На экране диалоговое окно Результат поиска решения (рис.18.).
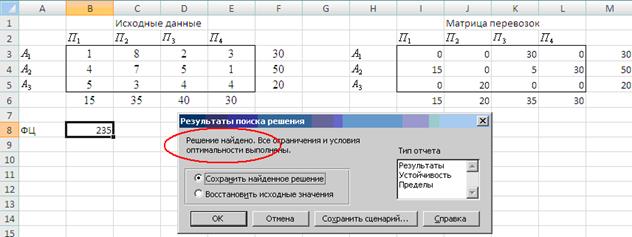
Рис.21. Решение найдено.
Найденный план перевозок означает, что общая стоимость перевозок составит 235 ден.ед., если
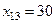 ед. груза перевести со станции 1 потребителю 3;
ед. груза перевести со станции 1 потребителю 3;
 ед. груза перевести со станции 2 потребителю 1;
ед. груза перевести со станции 2 потребителю 1;
 ед. груза перевести со станции 2 потребителю 3;
ед. груза перевести со станции 2 потребителю 3;
 ед. груза перевести со станции 2 потребителю 4;
ед. груза перевести со станции 2 потребителю 4;
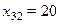 ед. груза перевести со станции 3 потребителю 2.
ед. груза перевести со станции 3 потребителю 2.
Неудовлетворены будут потребители 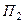 и
и  , т.к. они получат груза меньше, чем составляют их потребности. Так, например, потребность
, т.к. они получат груза меньше, чем составляют их потребности. Так, например, потребность 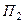 составляет 35 ед. груза (ячейка C6), а получит он только 20 ед. (ячейка J6).
составляет 35 ед. груза (ячейка C6), а получит он только 20 ед. (ячейка J6).
Остальные потребители удовлетворены полностью.
Вопросы:
1. Сколько груза должно быть перевезено из А2 в П1?
2. С кем работает поставщик А2?
3. С кем работает потребитель П4?
4. Измените модель, добавив условие:
1. Потребности П2 обязательно должны быть удовлетворены. (F=265)
2. Запрещены перевозки в направлении А2 –П3.(F=245)
3. В направлении А3—П1 необходимо перевезти не менее 5 тонн.(F=250)
4. Возможности А3 стали равны 50; (F=290)
Задача о назначениях
Известна матрица эффективности. Осуществить назначение продавцов по торговым точкам для достижения максимального объема продаж.
| Прода- вец | средний дневной объем продаж продуктов по торговым точкам, у.е. | |||

| 
| 
| 
| |

| ||||

| - | |||

| ||||

|
(назначение продавца  на торговую точку
на торговую точку  недопустимо по медицинским показаниям, т.е. в матрице эффективностей знаком «-» проставлен запрет назначений).
недопустимо по медицинским показаниям, т.е. в матрице эффективностей знаком «-» проставлен запрет назначений).
Решение.
Этап 1.
Построим математическую модель задачи о назначениях.
1. Введем управляющие переменные:
 - факт назначения ресурса
- факт назначения ресурса  на работу
на работу 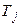 :
:
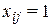 , если кандидат
, если кандидат  назначен на работу
назначен на работу 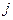 ,
,
 , если кандидат
, если кандидат  не назначен на работу
не назначен на работу 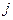 .
.
2. Объем продаж  -го продавца на
-го продавца на 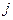 -ой торговой точке равны
-ой торговой точке равны  ,
,  ,
, 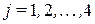 .
.
Функция цели - объем продаж по всем продавцам и всем торговым точкам - определяется выражением:
 , или
, или

3. Определим баланс задачи: имеется 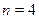 торговых точки и
торговых точки и 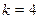 продавца, значит, задача является сбалансированной. Это означает, что на каждую торговую точку обязательно будет назначен продавец, причем только один, и каждый продавец получит назначение, причем только на одну торговую точку.
продавца, значит, задача является сбалансированной. Это означает, что на каждую торговую точку обязательно будет назначен продавец, причем только один, и каждый продавец получит назначение, причем только на одну торговую точку.
4. Построим систему ограничений.
По продавцам: каждый продавец будет назначен только на одну торговую точку, т.е. сумма назначений первого продавца ( ) будет равна 1. Аналогично для других продавцов. Получим систему ограничений:
) будет равна 1. Аналогично для других продавцов. Получим систему ограничений:
 или
или 
По торговым точкам: на каждую торговую точку будет назначен только один продавец. Следовательно, эти ограничения будут записаны в виде:
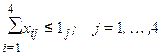 , или
, или 
Добавим ограничение 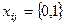 - двоичные переменные.
- двоичные переменные.
Кроме того, в задаче имеется дополнительное ограничение: запрет назначения продавца  на торговую точку
на торговую точку  , которое реализуется ограничением
, которое реализуется ограничением 
Этап 2.
1.Подготовим форму для ввода исходных данных (Рис. 22.).
В нашем примере матрица эффективности назначений продавцов по торговым точкам  вводится в ячейки блока В3:E6.
вводится в ячейки блока В3:E6.
Зарезервированы изменяемые ячейки H3:K6 - для создания матрицы назначений (размерность матрицы назначений должна совпадать с размерностью матрицы эффективности). В этих ячейках будут находиться оптимальные значения управляющих переменных  .
.

Рис. 22. Создание формы для ввода условий задачи.
2. Введем зависимость для целевой функции (рис. 23).
Оптимальное значение целевой функции будет помещено в ячейке В8
· Курсор в ячейку В8  .
.
· Мастер функций fx / Математические / СУММПРОИЗВ (В3:E6; H3:K6)

Рис. 23 Ввод зависимости целевой функции
2. Введем зависимости ограничений (рис 24.).
- вводим условия по продавцам:
· курсор в ячейку L3.  ;
;
- Мастер функций fx / Математические / СУММ (H3:K3)
- Скопировать ячейку L3 в L4, L5 и L6.
- вводим условия удовлетворения запросов по торговым точкам:
· курсор в ячейку Н7.  ;
;
- Мастер функций fx / Математические / СУММ(Н3:Н6);
- Скопировать ячейку Н7 в I7, J7 и K7.

Рис 24. Ввод формул для вычисления левых частей ограничений.
Этап 3. Запуск программы Поиск решений
· Назначение целевой ячейки: курсор в поле Установить целевую ячейку.  Левой кнопкой мыши щелкнуть на ячейке В8.
Левой кнопкой мыши щелкнуть на ячейке В8.
· Ввести направление целевой функции: максимальному значению.
· Ввести адреса искомых переменных: курсор в поле Изменяя ячейки.  . Выделить мышью ячейки Н3:К6.
. Выделить мышью ячейки Н3:К6.
· Ввести ограничения:
o курсор в поле Ограничения  . Выбрать режим Добавить
. Выбрать режим Добавить  .
.
o курсор в поле Ссылка на ячейку 
o выбрать мышью ячейки в L3: L6
o ввести знак ограничения =
o курсор в правое окно Ограничение  .
.
o Ввести 1
o Выбрать режим Добавить
o курсор в поле Ссылка на ячейку 
o выбрать мышью ячейки в Н7: К7
o ввести знак ограничения =
o курсор в правое окно Ограничение  .
.
o Ввести 1
o Добавим ограничение 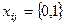 - двоичные переменные.
- двоичные переменные. 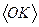

В результате окно Поиск решения будет выглядеть как показано на рисунке:

· Выбрать параметры модели: рис 4.
Этап 4. Выполнить (рис.25.).
На экране диалоговое окно Результат поиска решения.

Рис.25. Решение найдено.
Найденный план назначений означает, что суммарный объем продаж будет максимальным и составит 218у.е., если:
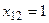 - продавец
- продавец  назначен на торговую точку
назначен на торговую точку  ;
;
 - продавец
- продавец  назначен на торговую точку
назначен на торговую точку  ;
;
 - продавец
- продавец  назначен на торговую точку
назначен на торговую точку 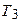 ;
;
 - продавец
- продавец  назначен на торговую точку
назначен на торговую точку 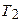 .
.
Все ограничения при этом выполнены.
Вопросы:
Измените модель, добавив условие:
1. На третьей точке обязательно должен работать продавец П2.(F=173)
2. Запрещено назначение продавца П1 на торговую точку Т2.(F=218)
3. Измените модель при условии, что закрыли IV торговую точку. (F=173)
4. В рамках несбалансированной задачи выполните условия:
1) Продавец П1 обязательно должен быть назначен на какую-либо торговую точку.(F=173)
2) Продавец П1 обязательно должен быть назначен на 2 торговую точку.(F=169)
Задачи для самостоятельного решения
Задание 1.
Компания занимается ремонтом дорог. Имеются экономические оценки транспортных затрат на перевозку 1 тонны песка с каждого карьера на каждый участок, известны объемы поставок по карьерам и объемы потребностей по участкам:
| Участки Карьеры | В1 | В2 | В3 | В4 | Предложение |
| К1 | |||||
| К2 | |||||
| К3 | - | ||||
| К4 | |||||
| Потребности |
Составить оптимальный план перевозок, обеспечивающий минимальные транспортные расходы.
Ответ:
| В1 | В2 | В3 | В4 | ||
| К1 | |||||
| К2 | |||||
| К3 | |||||
| К4 | |||||
| ФЦ= |
Задание 2.
Эффективность работы продавцов (объем продаж) в различных торговых точках приведена в таблице:
| Торговые точки продавец | I | II | III | IV |
| А | ||||
| В | ||||
| С |
Как осуществить назначение продавцов по торговым точкам, чтобы обеспечить максимальный объем продаж?
Ответ:
| I | II | III | IV | ||
| А | |||||
| В | |||||
| С | |||||
| ФЦ= |