
Если a1…an – числа, то это ур-е с постоянными коэфф..

 - характеристическое ур-е
- характеристическое ур-е
y''+a1y'+a2y=0 (диф ур-е 2го порядка),
λ2+a1λ+a2=0, где λ1= λ2

a21-4a2=0
λ1= λ2= 
1 решение: y1= 
Проверим, что y2=  - тоже решение
- тоже решение
y2=  ; y'2=
; y'2=  ;
;
y''2=  Получим:
Получим: 
Учтем, что λ1= 
y2=  -явл решением, ЧТД
-явл решением, ЧТД
Значит Y=  , где Y-общ решение
, где Y-общ решение
 11.Линейные ДУ с постоянными коэф и его хар ур-е. Вид общего решения в случае комплексных корней хар-го Ур-я (на примере ДУ 2го порядка)
11.Линейные ДУ с постоянными коэф и его хар ур-е. Вид общего решения в случае комплексных корней хар-го Ур-я (на примере ДУ 2го порядка)

Если a1…an – числа, то это ур-е с постоянными коэфф.. 

 - характеристическое ур-е
- характеристическое ур-е
y''+a1y'+a2y=0 (диф ур-е 2го порядка),
λ2+a1λ+a2=0, где λ1,2=α±iβ
y(x)=u(x)+iv(x); y'(x)=u'(x)+iv'(x)
u(x)-вещ часть
v(x) – мнимая часть
Теорема. L[y]=0®u(x), v(x)-решения
L[y]=L[u=iv]=L[u]+iL[v]=0®L[u]=L[v]=0
y1,2= e(α±β)x




Y=c1eαx·cosβx+c2eαx·sinβx
13.Нормальная система ДУ. Общее и частное решение. Задача Коши. Теорема существования и единственности решения. Линейная система ДУ
Формы записи: 1) F(x,y,y',…y(n-1))=0 – ДУ n-го порядка;
2) yn=f(x,y,…y(n-1));
3) F(x,y,y')=0; y'=f(x,y);
4) 
5) относительно разрешенного 
(4) и (5) – векторная форма записи систем ДУ

Частное решение для (6) - найти упорядоченный набор функций, при подстановке которых в систему ДУ, все уравнения обратятся в тождество.
 (y1(x),…yn(x)) – частное решение
(y1(x),…yn(x)) – частное решение
Решить ур-е (5) – найти вектор-функцию при подстановке к-рой в ур-ии получилось верное векторное тождество
Общее решение -множество всех решений
7)

Задача Коши для системы ДУ
Теорема суш-я
Если фун-я  непрерывна в т. М0(x0,y10,…y10),то задача Коши (6) имеет единственное решение у1(x)…yn(x) в окрестности точки U(x0)
непрерывна в т. М0(x0,y10,…y10),то задача Коши (6) имеет единственное решение у1(x)…yn(x) в окрестности точки U(x0)
Система лин. ДУ
Система линейна, когда ф-я линейна относительно у1, y2…yn
(5)-векторная форма
Y'=AY+B – матричная форма записи
14.Решение системы линейных однородных ДУ с постоянной.матрицей коэф. (случай различных ыещественных корней хар Ур-я)
Yʼ=A*Y
D-множ-во реш-й сист-ы, элем-ми кот-й явл.матричные функции.
Т.: множ.D-n мерное векторное пространство.
Его базис наз. фунд.сист.реш-й.Все элем-ты явл. лин.комбин-ми c1Y1+..+cnYn, где базис Y1..Yn.
Из опред век.прос-ва:1)если Y1,Y2 –реш-я, тоY1+Y2 тоже реш. 2)если Y – реш, то cY тож реш.
Опр-ль Вронского 
, если W=0, то матрицы Y1..Yn лин.завис.
Y имеет вид 
,
Yʼ= 
 =A*
=A* 
αλ=A*α, α-соб.вектор λ-соб.число; (A-λE)α=0 матрич.форма записи сист., если А-числа.
det(A-λE)=0 харктеристич.ур.сист., сист. не имеет реш-й.
Т.: если корни харак.ур. различны, то базисом множ. D будут вектора Yi=eλixαi.
Ряды.
1. Числовые ряды. Сходимость ряда. Необходтмое условие сходимости. Гармонический ряд.
Дана an последовательность, тогда  =a1+a2+..+an+.. –ряд.
=a1+a2+..+an+.. –ряд.
Справа – формальная сумма бесконечного числа чисел.
частичные суммы:Sn=a1,..Sn=a1+..+an
Сумма ряда-предел частичных сумм.
Ряд сходится, если сущ-ет предел частичных сумм, в противном случае расходится.
Необход.признак сход-ти: если ряд сходится, то предел общего члена равен нулю.
an=Sn-Sn-1
liman=lim(Sn-Sn-1)=limSn-limSn-1=Sn-Sn-1=0.
1+1/2+1/3+..+1/n –гармонический ряд. Задача:исслед.сход-ть ряда.
Sn=1+1/2+..1/n > ln(1+1/1)+ln(1+1/2)+//ln(1+1/n)=ln(2/1+3/2+..(n+1)/n)=ln(n+1).
Sn>ln(n+1)→∞ при n→∞. Предела нет, гарм. ряд расход
2. Геометрический ряд. Действия со соходящимися рядами
Геометрич.ряд - 
a+aq+aq2+..aqn-1.. –сумма членов геомет.прогрессии.
1)при a=0 S=0
2)Sn=a*(1-qn)/(1-q) при q≠1.
При |q|<1 сх. и S=a/(1-q)
При |q|>=1 расх. и предела нет.
Св-ва сход.рядов: 1) если ряд сх. и его сумма=S, то λ*ряд тоже сх. и его сумма=λ*S, т.е. если все члены ряда умножить на число, то его S умнож-ся на это число. 
Док-во: Sn=a1+..+an λa1+..+λan=λSn S=limSn λlimSn=λS. 2) сх.ряды можно складывать почленно  3) если ряд сх-ся, то сх-ся и ряд, получ-й из данного отбрасыванием конечного числа членов. Док-во: a1+..+an+.. ak+1+..+ak+n+.. Sn=a1..+an=Sk+σn-k σn-k частич.сумма limSn=lim(Sk+σn-k)=Sk+limσn-k если сущ. Первый предел, то сущ. и послед., и наоборот. 4) для того, чтобы ряд сх-ся, необходимо и достаточно, чтоб остаток ряда стремился к нулю. S=a1+..an, rn=an+1+an+2.., S=Sn+rn,
3) если ряд сх-ся, то сх-ся и ряд, получ-й из данного отбрасыванием конечного числа членов. Док-во: a1+..+an+.. ak+1+..+ak+n+.. Sn=a1..+an=Sk+σn-k σn-k частич.сумма limSn=lim(Sk+σn-k)=Sk+limσn-k если сущ. Первый предел, то сущ. и послед., и наоборот. 4) для того, чтобы ряд сх-ся, необходимо и достаточно, чтоб остаток ряда стремился к нулю. S=a1+..an, rn=an+1+an+2.., S=Sn+rn,  сх. ó rn→0. Док-во: Sn=S-rn, S=limSn=lim(S-rn)=S-limrn=0.
сх. ó rn→0. Док-во: Sn=S-rn, S=limSn=lim(S-rn)=S-limrn=0.
3.Ряды с положительными членами. Признак Даламбера.
Признаки сходимости:1.признак сравнения(1)  ; (2)
; (2)  ; 0≤a
; 0≤a  ≤b
≤b 
 -сход. =>
-сход. =>  -сход.
-сход.
 -расход.=>
-расход.=>  -расход.
-расход.
Док.-во: А  =а1+…+аn (частич сумма 1 ряда)
=а1+…+аn (частич сумма 1 ряда)
Bn=b1+…+bn
An≤ Bn, Аn, Bn-возрастают
(2) сход=> Bn ограничена числом В
В=limBn; An ≤ В=> An-возрас и ограничена и знач имеет предел
n-> 
. Признак Даламбера.
 , an>0,
, an>0,  =l
=l 
l<1 => ряд сход.
l>1 => ряд расход (при l=1 приз Далам ответа не дает)
Док-во: 1) l<1
 n≤N
n≤N  ≤q<1
≤q<1
a  ≤q
≤q 
a  ≤q
≤q  ≤q
≤q  an
an
a  ≤q
≤q  * an
* an
a  +a
+a  +…+a
+…+a  …(*)-сход по приз срав; остат 1 ряда
…(*)-сход по приз срав; остат 1 ряда
a  +a
+a  .q+…+a
.q+…+a  .q
.q 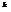 +…(**)-геометр ряд со знач<1=> сход
+…(**)-геометр ряд со знач<1=> сход
a  ≥a
≥a  n≥N
n≥N
если предел>1, то начиная с некоторого номера  ≥1=>
≥1=>  а
а  >0=> ряд расхож по необх признак
>0=> ряд расхож по необх признак
4.Интегральный признак Коши. Обощенно-гармонический ряд. Признаки сравнения рядов.
Интегральный признак Коши
 а
а 
Т.: Пусть члены ряда убывают и положит., и пусть ф-я f(n)=an, тогда ряд an сход, тогда и только тогда, когда интерг сход.
Док-во: Sn=a1+a2+…+an
Sn≥  f(x) dx, a2+a3…+a
f(x) dx, a2+a3…+a  <
< 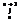 f(x) dx
f(x) dx
предполож, что ряд сход., тогда:  ≤Sn<S
≤Sn<S

 f(x) dx≤S=
f(x) dx≤S=  f(x) dx
f(x) dx
если I=  f(x) сход =>
f(x) сход =>  f(x) dx<I
f(x) dx<I
S  -a1<I, знач S
-a1<I, знач S  <а1+I => огранич и имеет lim, знач ряд сход.
<а1+I => огранич и имеет lim, знач ряд сход.
Обощенно-гармонический ряд.
Гармонич ряд наз след ряд: 1+ 
-исследов сход данного ряда:
ln(1+α)>α e=  (1+
(1+  )
) 
(1+  )
)  <e
<e
n ln (1+  )<1
)<1
ln(1+  )<
)< 
-запишем частич сумму:
Sn=1+  >ln(1+
>ln(1+  )+ln(1+
)+ln(1+  )+…+ln(1+
)+…+ln(1+  )=
)=
ln[  ]=ln(n+1)
]=ln(n+1)
Sn>ln(n+1) 
n 
гармонич ряд расход, общий член стремится к нулю
Признаки сравнения рядов.
1.признак сравнения
(1)  ; (2)
; (2)  ; 0≤a
; 0≤a  ≤b
≤b 
 -сход. => -сход.
-сход. => -сход.
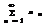 -расход.=>
-расход.=>  -расход.
-расход.
Док.-во: А  =а1+…+аn (частич сумма 1 ряда)
=а1+…+аn (частич сумма 1 ряда)
Bn=b1+…+bn
An≤ Bn, Аn, Bn-возрастают
(2) сход=> Bn ограничена числом В
В=limBn; An ≤ В=> An-возрас и ограничена и знач имеет предел
n-> 
5. Знакопеременные ряды. Достаточный признак сходимости. Абсолютная и условная сходимость.
Знакопеременные ряды.
(1)  (2)
(2) 
если его члены не имеют произв знач ряд (1) сход абсолют, если схож ряд (2)
Т.: Если ряд (1) сход абсолют, то он сход
Док-во: Sn=a1+…+an=Sn’-Sn”, Sn’,Sn” ≥0
Sn’-сумм положит слаг из 1-х т шт
(-Sn”)-сумм отриц слаг
 -сумм ряд (2)
-сумм ряд (2)
 =Sn’+Sn”
=Sn’+Sn”
Если ряд (2) сход => что  <δ(огранич), а знач Sn’ и Sn”-огранич (<
<δ(огранич), а знач Sn’ и Sn”-огранич (<  )=>Sn’-S’; Sn”
)=>Sn’-S’; Sn”  S”
S”
 Sn=
Sn=  (Sn’-Sn”)=S’-S”
(Sn’-Sn”)=S’-S”
замечания: сход ряда не след его абсол
при измен порядка слаг в усл-сход ряду, его сумм мож изменит, т.е.какое бы ни было S можно так изменит поряд слаг. в усл-сход ряду, что его сумм=S
Достаточный признак сходимости
Если an не стремится к нулю, то ряд не может быть сход-ся, т.е. он расход-ся.
Пример:  => ряд расход, ибо его общ член an=
=> ряд расход, ибо его общ член an=  при n
при n  , стремится к 1/100 и знач не стремит к нулю. !!! стремление n-го члена ряда к 0 не яв-ся достаточным для сход ряда !!!
, стремится к 1/100 и знач не стремит к нулю. !!! стремление n-го члена ряда к 0 не яв-ся достаточным для сход ряда !!!
Абсолютная и условная сходимость.
Есл ряд, состав из абсолют велич член дан ряда, сх-ся, то сх-ся и дан ряд
Ряд наз-ся сход относ(усл), есл он сход, а ряд из его модул расход.
6. Теорема Лейбница
Знакочеред. ряд с убыв член сход-ся:  an,
an,  <a1, an>0
<a1, an>0
Есл предел общ чл=0  =0 =>
=0 => 
 an-ax, a
an-ax, a  >an, an>0
>an, an>0
Док-во S2n=(a1-a2)+(a5-a4)+…+(a  -a2n); S2n>0, S2n-возрас
-a2n); S2n>0, S2n-возрас
S2n=a1(a2-a3)-(a4-a5)-…-(a  -a
-a  )-a2n
)-a2n
S2n<a1-огранич => S2n  S
S  =S+0
=S+0
Сл1:  an; a
an; a  <an; an>0
<an; an>0
 Sn=S=> S<ax
Sn=S=> S<ax
Сл2: |S-Sn|< a  абсолют ошибка замены S на Sn и она <1-го отбрас чл Sn
абсолют ошибка замены S на Sn и она <1-го отбрас чл Sn  S
S
7.Функциональные ряды.
Это ряд вида: U1(x)+U2(x)+…+Un(x)…(1)
S1(x)=U1(x); Sn(x)=U1(x)+…+Un(x)
S(x)=  Sn(x)
Sn(x)
Обл сход ряд(1)-мн-во Х, для кот ряд(1)сход. Это есть обл опред ф-и f(x)
8. Степенный ряды.
Степенным рядом наз-ся функц ряд (3) a0+a1(x-a)+a2(x-a) 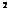 +…+an(x-a)
+…+an(x-a)  чл кот суть произв пост а0,а1,ат на степен ф-ции с цел показ степен от разнос х-а
чл кот суть произв пост а0,а1,ат на степен ф-ции с цел показ степен от разнос х-а
Теорема Абиля:
(2)а0+а1х+…+аnx+…
а) есл (2)сход при х0, то он сход при |x|<|x0|
б)есл (2) расход при х0, то он расход при |x|>|x0|
Док-во: а0+а1х+…+аnx  +…
+…
|a0|+|a1||x|+…+|an||x|  +…=|a0|+|a1x0||
+…=|a0|+|a1x0||  |+…+|anx
|+…+|anx  0||
0||  |
|  +…(*)
+…(*)
 -сход =>
-сход =>  =>0=>|
=>0=>|  |<M
|<M
<M(1+|  |+…+|
|+…+|  |
|  -q=|
-q=|  | -геомет ряд со знач сход при q=1=> ряд(*) сход по приз срав с геом ряд; а первон ряд сход абсол
| -геомет ряд со знач сход при q=1=> ряд(*) сход по приз срав с геом ряд; а первон ряд сход абсол
есл ряд(2) расход при х’0 и пусть при |x|>|x0|-сход
(х-сх-ся=> x’0-сход это противор)
Радиус и интервал сход-ти степен ряда:
Радиусом сход-ти степен ряда наз-ся такое число R, что для всех x, |x|<R, степен ряд сход, я для всех x, |x|>R, расход. Интервал (-R,R)-интервал сход-ти