Постановка задачи
Цель данной курсовой работы - реализация численного интегрирования функции двух переменных.
Для некоторых подынтегральных функций интеграл можно вычислить аналитически или найти в справочниках. Однако в общем случае первообразная может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами подынтегральные функции не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов. Наиболее общеупотребительными приближенными методами вычисления одномерных определенных интегралов являются, так называемые, "классические" методы численного интегрирования: метод прямоугольников, метод ячеек, метод трапеций, метод парабол.
Одним из простейших способов вычисления двойного интеграла является метод ячеек, основанный на суммировании элементарных площадей, на которые разбивается вся площадь под функцией.
Для решения примеров воспользуемся пакетом Mathcad.
Пример 1.
Вычислить интеграл
.
Решение:
Результат вычисления
Пример 2.
Вычислить интеграл
.
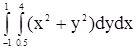Решение:
Результат вычисления
Пример 3.
Вычислить интеграл
.
Решение:
Результат вычисления
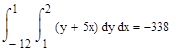
Математические и алгоритмические основы решения задачи
Понятие двойного интеграла
Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f (x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций.
Обозначение двойного интеграла
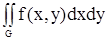
Геометрический смысл двойного интеграла
Для того, чтобы понять, что же представляет из себя двойной интеграл с геометрической точки зрения, давайте посмотрим на рисунок ниже.
Рисунок 1 - Геометрический смысл двойного интеграла
Итак, пусть в пространстве мы имеем некоторое тело (криволинейный цилиндр [в отличие от криволинейной трапеции в определенном интеграле]), ограниченное сверху поверхностью f (x,y), по бокам - некоторой цилиндрической поверхностью (образующие которой параллельны оси OZ), а снизу плоскостью X0Y.
Не углубляясь особо в теорию, возьмем из нее главное: Геометрический смысл двойного интеграла: при неотрицательной функции f (x,y), двойной интеграл по области D представляет из себя объем криволинейного цилиндра, который построен на области D и ограничен сверху поверхностью z=f (x,y).
Метод ячеек
Одним из простейших способов численного интегрирования функции двух переменных является метод ячеек.
Рассмотрим сначала случай, когда областью интегрирования G интеграла I= 
является прямоугольник: 
, 
.
По теореме о среднем найдём среднее значение функции f (x,y):
S= (b-a) (d-c). (1)
Рисунок 2 - Метод ячеек
Будем считать, что среднее значение приближённо равно значению функции в центре прямоугольника, т.е.
.
Тогда из (1) получим выражение для приближённого вычисления двойного интеграла:
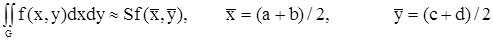(2)
Точность этой формулы можно повысить, если разбить область G на прямоугольные ячейки D 
ij (рис.1):
xi-1 
i (i=1,2,…,M),
yi-1 
i (j=1,2,…,N).
Применяя к каждой ячейке формулу (3), получим
òòDGijf (x,y) dxdy»¦ (
) DxiDyi.
Суммируя эти выражения по всем ячейкам, находим значение двойного интеграла:
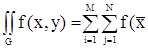I,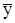 
j) (3)
В правой части стоит интегральная сумма; поэтому при неограниченном уменьшении периметров ячеек (или стягивания их в точки) эта сумма стремится к значению интеграла для любой непрерывной функции f (x,y). Можно показать, что погрешность такого приближения интеграла для одной ячейки оценивается соотношением
Rij» 
DxiDyj 
.
Суммируя эти выражения по всем ячейкам и считая все их площади одинаковыми, получаем оценку погрешности метода ячеек в виде
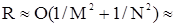O (Dx2+Dy2).
Таким образом, формула (3) имеет второй порядок точности. Для повышения точности можно использовать обычные методы сгущения узлов сетки. При этом по каждой переменной шаги уменьшают в одинаковое число раз, т.е. отношение M/N остаётся постоянным.
Если область G непрямоугольная, то в ряде случаев её целесообразно привести к прямоугольному виду путём соответствующей замены переменных. Например, пусть область задана в виде криволинейного четырёхугольника: 
, 
. Данную область можно привести к прямоугольному виду с помощью замены
, 
.
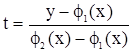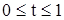Кроме того, формула (3) может быть обобщена и на случай более сложных областей.
Функциональные модели решения задачи
Функциональные модели решения задачи представлены на рисунках 3 - 5.
Используемые обозначения:
f - интегрируемая функция;
ax - начальный предел интегрирования по x;
bx - конечный предел интегрирования по x;
ay - начальный предел интегрирования по y;
by - конечный пределе интегрирования по y;
g - количество ячеек;
h1 - ширина ячейки;
h2 - высота ячейки;
S - площадь ячейки;
I - интеграл от функции f;
x, y - координаты центра ячейки.
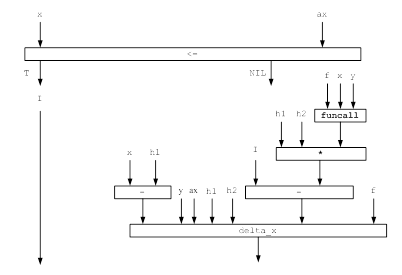
Рисунок 3 - Функциональная модель решения задачи для функции sum_delt
Рисунок 4 - Функциональная модель решения задачи для функции sum_delt
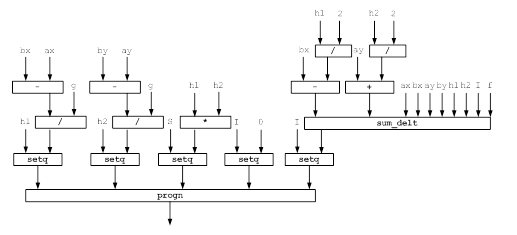
Рисунок 5 - Функциональная модель решения задачи для функции double_integral