БОГДАНОВ А.Е.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К самостоятельной работе
По дисциплине
“ ВЫСШАЯ МАТЕМАТИКА “
(Линейная алгебра и аналитическая геометрия)
для студентов дневной формы обучения специальностей
направления 6.050102 “Компьютерная инженерия”
УТВЕРЖДЕНО
на заседании кафедры
высшей и прикладной
математики
Протокол № 4 от 05.12.2007г.
Северодонецк 2007
УДК 516
Методические указания к самостоятельной работе по дисциплине “Высшая математика “(Линейная алгебра и аналитическая геометрия) для студентов дневной формы обучения специальностей направления 6.050102 “Компьютерная инженерия”.(электронное издание)/Сост. А.Е.Богданов -Северодонецк: Изд-во ТИ ВНУ им. Владимира Даля, 2007. – 56 с.
Составлено на основании программы математических дисциплин для инженерно-технических специальностей высших учебных заведений.
| Составитель: | А.Е.Богданов, доцент |
| Ответственный за выпуск: | О.В. Поркуян, доцент |
| Рецензент: | А.Н.Иванов, доцент |
ОГЛАВЛЕНИЕ
Программа ………………………………………………………... 4
Индивидуальные задания………………………………………… 6
Пример выполнения задания ……………………………………. 45
Литература ………………………………………………………… 55
ПРОГРАММА
1. Определители 2-ого и 3-его порядков и их свойства.
2. Системы линейных уравнений. Правило Крамера.
3. Системы линейных уравнений. Метод Гаусса.
4. Матрицы. Основные определения.
5. Действия над матрицами.
6. Обратная матрица.
7. Решение систем линейных уравнений матричным методом.
8. Ранг матрицы. Эквивалентные матрицы.
9. Исследование систем линейных уравнений. Теорема Кронекера- Капелли.
10. Векторы. Основные понятия и определения.
11. Двумерные и трехмерные векторы.
12. Линейно независимые и линейно зависимые векторы. Базис.
13. Скалярное произведение векторов и его свойства.
14. Векторное произведение векторов и его свойства.
15. Смешанное произведение векторов и его свойства.
16. Уравнение прямой с угловым коэффициентом: прямая, проходящая через заданную точку, через две заданных точки.
17. Уравнение прямой с угловым коэффициентом: угол между прямыми, условия параллельности и перпендикулярности прямых.
18. Общее уравнение прямой: уравнение прямой, проходящей через заданную точку.
19. Общее уравнение прямой: угол между прямыми, условия параллельности и перпендикулярности прямых.
20. Общее уравнение плоскости: уравнение плоскости, проходящей через заданную точку, через три заданные точки, уравнение плоскости в отрезках.
21. Плоскость: угол между плоскостями, условия параллельности и перпендикулярности плоскостей.
22. Прямая в пространстве.
23. Прямая и плоскость в пространстве.
24. Кривые 2-ого порядка: окружность, эллипс.
25. Кривые 2-ого порядка: гипербола.
26. Кривые 2-ого порядка: парабола.
27. Классификация кривых 2-ого порядка.Приведение общего уравнения кривой 2-ого порядка к каноническому виду.
28. Поверхности 2-ого порядка: сфера, эллипсоид, однополостный и двуполостный гиперболоиды.
29. Поверхности 2-ого порядка: эллиптический и гиперболический параболоиды, конус 2-ого порядка.
30. Цилиндры 2-ого порядка.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
ВАРИАНТ № 1
1. Решить систему уравнений по правилу Крамера, методом Гаусса,
матричным методом
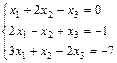
2. Выполнить действия над матрицами
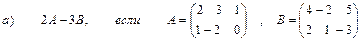
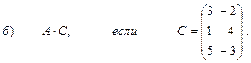
3. Даны вершины 
треугольника АВС:
; 2; 4), В (-2; 0; 3), С (2; -4; 1).
Найти: а) угол АВС;
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(4; 2; 5), А 2(0; 7; 2), А 3(0; 2; 7),
А 4(1; 5; 0). Найти объем пирамиды.
5. Даны вершины треугольника А (3;1), В (-4;-1), С (3;8). Составить уравнение высоты, опущенной из вершины А на сторону ВС.
6. Даны координаты вершин пирамиды: А (1;3;6), В (2;2;1), С (-1;0;1),
D (-4;6;-3). Найти длину высоты, опущенной из вершины А на грань ВСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
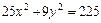8. Составить уравнение параболы, которая имеет фокус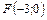 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 2
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
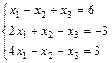
2. Выполнить действия над матрицами
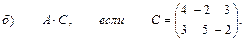
3. Даны вершины треугольника АВС:
А (3; -2; 1), В (1; 4; 3), С (0;-2; 5).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(4; 4; 10), А 2(4; 10; 2), А 3(2; 8; 4),
А 4(9; 6; 9). Найти объем пирамиды.
5. Даны вершины треугольника А (1;-2), В (0;3), С (-1;2). Найти расстояние от вершины В до стороны АС.
6. Даны координаты вершин пирамиды: А (-4;2;6), В (2;-3;0), С (-10;5;8),
D (-5;2;-4). Составить уравнение грани АВС в отрезках и найти расстояние от вершины D до грани АВС.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
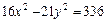8. Составить уравнение параболы, которая имеет фокус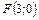 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 3
1. Решить систему уравнений по правилу Крамера, методом Гаусса и матричным методом
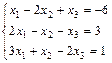
2. Выполнить действия над матрицами
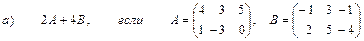
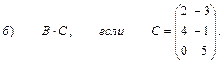
3. Даны вершины треугольника АВС:
А (4; 2; 1), В (-2;!; 0), С (1; -2; 2).
Найти: а) угол ВАС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(4; 6; 5), А 2(6; 9; 4), А 3(2; 10; 10),
А 4(7; 5; 9). Найти объем пирамиды.
5. Даны вершины треугольника А (0;1), В (3;4), С (-2;0). Составить уравнения его сторон.
6. Даны координаты вершин пирамиды: А (7;2;4), В (7;-1;-2), С (-3;3;1),
D (-4;2;1). Найти угол между гранями АВС и ВСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
8. Составить уравнение параболы, которая имеет фокус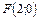 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 4
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
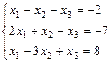
2. Выполнить действия над матрицами
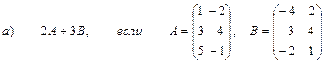
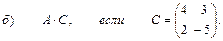
3. Даны вершины треугольника АВС:
А (1; 3; 4), В (2; 0; -3), С (3; -1; 2).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(3; 5; 4), А 2(8; 7; 4), А 3(5; 10; 4),
А 4(4; 7; 8). Найти объем пирамиды.
5. Даны вершины треугольника А (2;1), В (1;3), С (-1;4). Найти угол между сторонами АВ и АС.
6. Даны координаты вершин пирамиды: А (2;1;4), В (-1;5;-2), С (-7;-3;2),
D (-6;-3;6). Составить уравнение плоскости, проходящей через вер-шину А параллельно грани ВСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
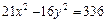8. Составить уравнение параболы, которая имеет фокус 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 5
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
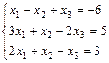
2. Выполнить действия над матрицами
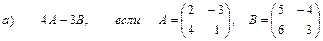
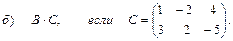
3. Даны вершины треугольника АВС:
А (6; -5; 7), В (8; 5; 4), С (5; 6; -5).
Найти: а) угол ВАС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(10; 6; 6), А 2(-2; 8; 2), А 3(6; 8; 9),
А 4(7; 10; 3). Найти объем пирамиды.
5. Даны вершины треугольника А (1;4), В (2;-3), С (0;-4). Составить уравнения его сторон в отрезках.
6. Даны координаты вершин пирамиды: А (-1;-5;2), В (-6;0;-3), С (3;6;-3),
D (-10;6;7). Проверить условие перпендикулярности между гранями АВС и ВСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
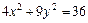8. Составить уравнение параболы, которая имеет фокус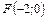 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 6
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
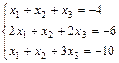
2. Выполнить действия над матрицами
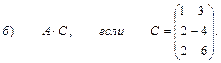
3. Даны вершины треугольника АВС:
А (3; 0; 4), В (5; 2; 1), С (2; 3; 0).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(1; 8; 2), А 2(3; 2; 6), А 3(5; 7; 4),
А 4(4; 10; 9). Найти объем пирамиды.
5. Даны вершины треугольника А (0;5), В (-2;3), С (1;2). Найти длину перепендикуляра, опущенного из вершины А на сторону ВС.
6. Даны координаты вершин пирамиды: А (0;-1;-1), В (-2;3;5), С (1;-5;-9),
D (-1;-6;3). Составить уравнение плоскости, проходящей через вер-шину А параллельно векторам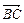 
и 
.
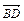7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
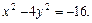
8. Составить уравнение параболы, которая имеет фокус 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 7
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
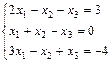
2. Выполнить действия над матрицами
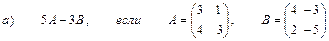
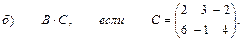
3. Даны вершины треугольника АВС:
А (3; 2; 4), В (2; 1; 5), С (2; -1; 0).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(6; 6; 5), А 2(4; 9; 5), А 3(4; 6; 11),
А 4(6; 9; 3). Найти объем пирамиды.
5. Даны вершины треугольника А (1;2), В (1;4), С (-2;3). Составить уравнение прямой,проходящей через вершину А параллельно стороне ВС. ящей через вершину
6. Даны координаты вершин пирамиды: А (5;2;0), В (2;5;0), С (1;2;4),
D (-1;1;1). Составить уравнение сечения пирамиды, проходящего через вершину А перпендикулярно ребру СD. Найти длину этого ребра.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
8. Составить уравнение параболы, которая имеет фокус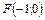 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 8
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
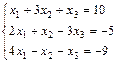
2. Выполнить действия над матрицами
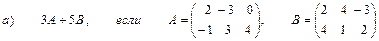
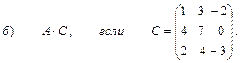
3. Даны вершины треугольника АВС:
А (4; 2; 3), В (5; 1; 2), С (0; 2; -1).
Найти: а) угол САВ,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(7; 2; 2), А 2(5; 7; 7), А 3(5; 3; 1),
А 4(2; 3; 7). Найти объем пирамиды.
5. Даны вершины треугольника А (2;4), В (-1;3), С (0;5). Составить уравнение прямой, проходящей через вершину А параллельно вектору 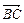.ящей через вершину
6. Даны координаты вершин пирамиды: А (2;-1;-2), В (1;2;1), С (5;0;-6),
D (-10;9;-7). Найти длину высоты, опущенной из вершины В на грань АСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
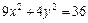8. Составить уравнение параболы, которая имеет фокус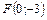 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 9
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
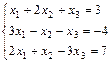
2. Выполнить действия над матрицами
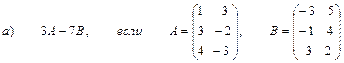
3. Даны вершины треугольника АВС:
А (0; 1; 3), В (3; 2; 4), С (5; 3; 4).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(8; 6; 4), А 2(10; 5; 5), А 3(5; 6; 8),
А 4(8; 10; 7). Найти объем пирамиды.
5. Даны вершины треугольника А (-1;5), В (0;4), С (1;3). Составить уравнение прямой, проходящей через вершину А перпендикулярно вектору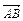 
.ящей через вершину
6. Даны координаты вершин пирамиды: А (-2;0;-4), В (-1;7;1), С (4;-8;-4),
D (1;-4;6). Составить уравнение грани АВD в отрезках и найти расстояние от вершины С до грани АВD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
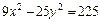8. Составить уравнение параболы, которая имеет фокус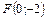 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 10
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
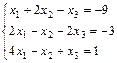
2. Выполнить действия над матрицами
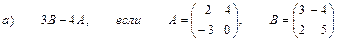
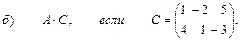
3. Даны вершины треугольника АВС:
А (2; 3; 1), В (3; 2; -2), С (4; 3; 5).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(7; 7; 3), А 2(6; 5; 8), А 3(3; 5; 8),
А 4(8; 4; 1). Найти объем пирамиды.
5. Даны вершины треугольника А (-3;4), В (-1;5), С (2;8). Найти длину
высоты, опущенной из вершины А на сторону ВС.
6. Даны координаты вершин пирамиды: А (14;4;5), В (-5;-3;2), С (-2;-6;8),
D (-2;2;-1). Найти угол между гранями АВD и АСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
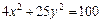8. Составить уравнение параболы, которая имеет фокус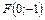 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 11
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
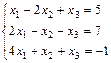
2. Выполнить действия над матрицами
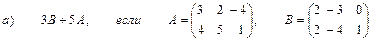
3. Даны вершины треугольника АВС:
А (4; 3; 5), В (3; 2; 4), С (0; 1; 3).
Найти: а) угол САВ,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(2; 0; 0), А 2(-2; 0; -1), А 3(1; 4; 2),
А 4(3; 0; 6). Найти объем пирамиды.
5. При каком значении а прямая
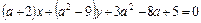
параллельна оси абсцисс. Написать уравнение прямой.
6. Даны координаты вершин пирамиды: А (1;2;0), В (3;0;-3), С (5;2;6),
D (8;4;-9). Составить уравнение плоскости, проходящей через вер-шину В параллельно грани АСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
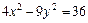8. Составить уравнение параболы, которая имеет фокус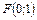 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 12
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
2. Выполнить действия над матрицами
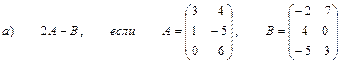
3. Даны вершины треугольника АВС:
А (0; 2; 4), В (4; 1; 3), С (5; 2; -1).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(1; 2; 3), А 2(2; 0; 0), А 3(3; 2; 5),
А 4(4; 0; 0). Найти объем пирамиды.
5. Даны вершины треугольника А (-2;5), В (0;6), С (1;4). Составить уравнение медианы, проведенной из вершины В на сторону АС.
6. Даны координаты вершин пирамиды: А (2;-1;2), В (1;2;-1), С (3;2;1),
D (-4;2;5). Проверить условие перпендикулярности между гранями АВС и АСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
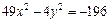8. Составить уравнение параболы, которая имеет фокус 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 13
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
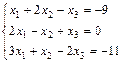
2. Выполнить действия над матрицами
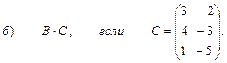
3. Даны вершины треугольника АВС:
А (2; 2; 3), В (4; -1; 1), С (5; 0; 4).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(-2; 0; 2), А 2(0; 0; 4), А 3(3; 2; 5),
А 4(-1; 3; 2). Найти объем пирамиды.
5. Доказать, что прямые
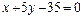и 
пересекаются. Найти точку их пересечения.
6. Даны координаты вершин пирамиды: А (1;1;2), В (-1;1;3), С (2;-2;4),
D (-1;0;-2). Составить уравнение плоскости, проходящей через вер-шину В параллельно векторам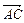 
и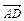 
.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
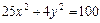8. Составить уравнение параболы, которая имеет фокус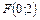 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 14
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
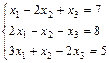
2. Выполнить действия над матрицами
3. Даны вершины треугольника АВС:
А (0; 1; 2), В (-2; -1; 3), С (1; -4; 0).
Найти: а) угол САВ,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(3; 0; 6), А 2(1; -3; 2), А 3(3; 2; 5),
А 4(2; 2; 3). Найти объем пирамиды.
5. Даны вершины треугольника А (3;4), В (-2;4), С (-1;5). Составить уравнение высоты, опущенной из вершины В на сторону АС.
6. Даны координаты вершин пирамиды: А (2;3;1), В (4;1;-2), С (6;3;7),
D (7;5;3). Составить уравнение сечения пирамиды, проходящего через вершину В перпендикулярно ребру АС. Найти длину этого ребра.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
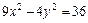8. Составить уравнение параболы, которая имеет фокус 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 15
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
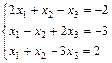
2. Выполнить действия над матрицами
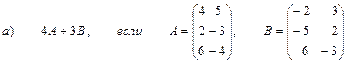
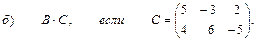
3. Даны вершины треугольника АВС:
А (1; -4; 0), В (0;2; 1), С (-1; -2; 3).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(-2; 1; 6), А 2(3; 2; 7), А 3(2; 2; 5),
А 4(6; 1; 5). Найти объем пирамиды.
5. Даны вершины треугольника А (1;5), В (-1;3), С (2;4). Составить уравнение медианы, проведенной из вершины А на сторону ВС.
6. Даны координаты вершин пирамиды: А (1;1;-1), В (2;3;1), С (3;2;1),
D (5;9;-8). Найти длину высоты, опущенной из вершины С на грань АВD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
8. Составить уравнение параболы, которая имеет фокус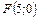 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 16
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
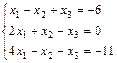
2. Выполнить действия над матрицами
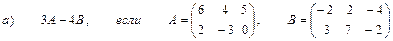
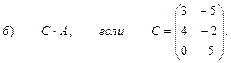
3. Даны вершины треугольника АВС:
А (0; 1; 3), В (-3; 2; -1), С (0; -2; 1).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(-1; 3; 0), А 2(2; 0; 0), А 3(4; -1; 2),
А 4(3; 2; 7). Найти объем пирамиды.
5. Даны вершины треугольника А (-2;1), В (2;4), С (1;5). Найти расстояние от вершины А до стороны ВС.
6. Даны координаты вершин пирамиды: А (1;2;0), В (3;5;4), С (6;0;1),
D (2;4;3). Составить уравнение грани АСD в отрезках и найти расстояние от вершины В до грани АСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
8. Составить уравнение параболы, которая имеет фокус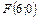 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 17
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
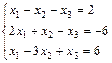
2. Выполнить действия над матрицами
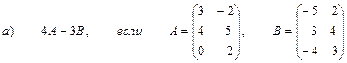
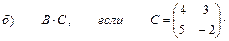
3. Даны вершины треугольника АВС:
А (0; 3; 1), В (2; -1; -3), С (1; 0; -2).
Найти: а) угол САВ,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(6; 1; 5), А 2(5; 1; 0), А 3(-4; 1; -2),
А 4(-6; 0; 5). Найти объем пирамиды.
5. Даны вершины треугольника А (-2;5), В (0;4), С (1;6). Найти угол между сторонами АВ и ВС.
6. Даны координаты вершин пирамиды: А (1;1;-1), В (3;2;1), С (0;3;0),
D (3;0;1). Составить уравнение плоскости, проходящей через вер-шину С параллельно грани АВD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
8. Составить уравнение параболы, которая имеет фокус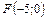 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 18
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
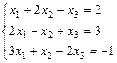
2. Выполнить действия над матрицами
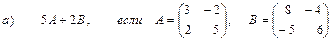
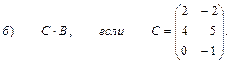
3. Даны вершины треугольника АВС:
А (3; 0; -3), В (-1; 2; 1), С (1; -2; 0).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(1; -1; 6), А 2(-5; -1; 0), А 3(4; 0; 0),
А 4(2; 2; 5). Найти объем пирамиды.
5. Даны вершины треугольника А (-4;5), В (0;-4), С (1;3). Составить уравнение прямой, проходящей через вершину В параллельно стороне АС. ящей через вершину
6. Даны координаты вершин пирамиды: А (1;1;-2), В (-2;2;1), С (1;-2;-3),
D (4;-1;1). Найти угол между гранями АВС и АВD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
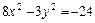8. Составить уравнение параболы, которая имеет фокус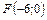 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 19
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
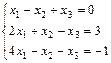
2. Выполнить действия над матрицами
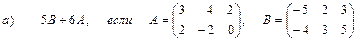
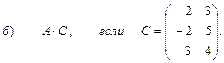
3. Даны вершины треугольника АВС:
А (1; -2; 2), В (3; 0; -1), С (0; 1; -2).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(0; 4; -1), А 2(3; 1; 4), А 3(-1; 6; 1),
А 4(-1; 1; 6). Найти объем пирамиды.
5. Даны вершины треугольника А (-3;6), В (-1;-4), С (2;5). Найти дли-ну перепендикуляра, опущенного из вершины В на сторону АС.
6. Даны координаты вершин пирамиды: А (-1;1;3), В (1;-1;5), С (1;3;1),
D (1;-1;1). Проверить условие перпендикулярности между гранями ВСD и АСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
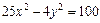8. Составить уравнение параболы, которая имеет фокус 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 20
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
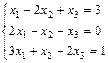
2. Выполнить действия над матрицами
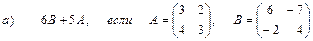
3. Даны вершины треугольника АВС:
А (1; 0; 2), В (0; -1; 3), С (0; -3; -2).
Найти: а) угол САВ,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(8; 5; 8), А 2(3; 3; 9), А 3(6; 9; 1),
А 4(1; 7; 3). Найти объем пирамиды.
5. Даны вершины треугольника А (-2;7), В (-1;6), С (1;3). Составить уравнение прямой, проходящей через вершину В параллельно вектору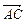 
.ящей через вершину
6. Даны координаты вершин пирамиды: А (-1;1;1), В (1;-2;2), С (5;-5;3),
D (1;0;3). Составить уравнение сечения пирамиды, проходящего через вершину C перпендикулярно ребру АD. Найти длину этого ребра.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка.Сделать рисунок
.
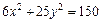8. Составить уравнение параболы, которая имеет фокус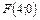 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 21
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
2. Выполнить действия над матрицами
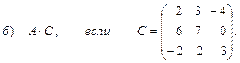
3. Даны вершины треугольника АВС:
А (2; 0; 1), В (3; -1; 0), С (-2; 0; -3).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(6; 4; 8), А 2(3; 5; 4), А 3(5; 8; 3),
А 4(1; 9; 9). Найти объем пирамиды.
5. Даны вершины треугольника А (-1;8), В (2;0), С (1;-6). Составить уравнение прямой, проходящей через вершину В перпендикулярно вектору 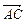.ящей через вершину
6. Даны координаты вершин пирамиды: А (-2;-3;2), В (2;3;-2), С (0;1;6),
D (1;0;3). Найти длину высоты, опущенной из вершины D на грань АВС.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
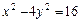8. Составить уравнение параболы, которая имеет фокус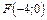 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 22
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
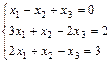
2. Выполнить действия над матрицами
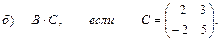
3. Даны вершины треугольника АВС:
А (-2; -1; 1), В (1; 0; 2), С (3; 1; 2).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(3; 6; 7), А 2(2; 4; 3), А 3(7; 6; 3),
А 4(4; 9; 3). Найти объем пирамиды.
5. Даны вершины треугольника А (-1;7), В (2;5), С (-1;8). Найти длину
высоты, опущенной из вершины В на сторону АС.
6. Даны координаты вершин пирамиды: А (2;-1;3), В (3;1;2), С (5;-5;4),
D (1;3;-8). Составить уравнение плоскости, проходящей через вер-шину С параллельно векторам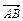 
и .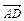
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
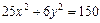8. Составить уравнение параболы, которая имеет фокус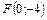 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 23
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
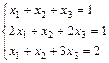
2. Выполнить действия над матрицами
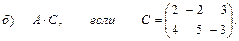
3. Даны вершины треугольника АВС:
А (0; 1; -1), В (1; 0; -4), С (2; 1; 3).
Найти: а) угол САВ,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(6; 9; 2), А 2(9; 5; 5), А 3(-3; 7; 1),
А 4(5; 7; 8). Найти объем пирамиды.
5. При каком значении а прямая
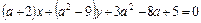
параллельна оси ординат. Написать уравнение прямой.
6. Даны координаты вершин пирамиды: А (-1;2;-1), В (1;-2;2), С (-1;0;3),
D (2;1;4). Составить уравнение грани ВСD в отрезках и найти расстояние от вершины А до грани ВСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
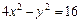8. Составить уравнение параболы, которая имеет фокус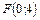 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 24
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
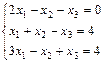
2. Выполнить действия над матрицами
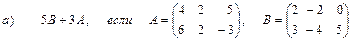
3. Даны вершины треугольника АВС:
А (2; 1; 3), В (1; 0; 2), С (-2; -1; 1).
Найти: а) угол АВС,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(3; 9; 8), А 2(0; 7; 1), А 3(4; 1; 5),
А 4(4; 6; 3). Найти объем пирамиды.
5. Доказать, что прямые
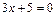и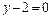 
пересекаются. Найти точку их пересечения.
6. Даны координаты вершин пирамиды: А (3;-1;1), В (5;-2;2), С (6;1;3),
D (4;-3;2). Найти угол между гранями АВD и ВСD.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
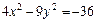8. Составить уравнение параболы, которая имеет фокус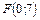 
и проходит через начало координат. Сделать рисунок.
ВАРИАНТ № 25
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
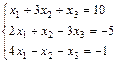
2. Выполнить действия над матрицами
3. Даны вершины треугольника АВС:
А (-2; 0; 2), В (2; -1; 1), С (3; 0; -3).
Найти: а) угол ВСА,
б) площадь треугольника АВС.
4. Задана пирамида с вершинами А 1(5; 8; 2), А 2(3; 5; 10), А 3(3; 8; 4),
А 4(5; 5; 4). Найти объем пирамиды.
5. Даны вершины треугольника А (-2;8), В (1;-5), С (2;8). Составить уравнение высоты, опущенной из вершины С на сторону АВ.
6. Даны координаты вершин пирамиды: А (5;-1;4), В (6;1;7), С (7;-2;3),
D (6;2;8). Составить уравнение плоскости, проходящей через вер-шину D параллельно грани АВС.
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
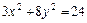8. Составить уравнение параболы, которая имеет