Пример решения задачи №3

ЗАДАЧА № 3

 

К стальному брусу круглого поперечного сечения приложены четыре крутящих момента , три из которых известны.

Требуется:

1) установить, при каком значении момента Х угол поворота правого кон­це­вого сечения равен нулю;

2) при найденном значении Х построить эпюру крутящих моментов;

3) при заданном значении допускаемого напряжения [t] определить диа­метр вала из условия его прочности и округлить величину диаметра до бли­жай­шей большей стандартной величины, равной 30, 35, 40, 45, 50, 60, 80, 90, 100 мм;

4) проверить, выполняется ли условие жесткости бруса при выбранном диа­метре, если допускаемый угол закручивания 1 град/м;

5) построить эпюру углов закручивания.

Для всех вариантов принять модуль сдвига для стали

Числовые данные берутся из табл. 3, расчетные схемы - по рис. 6.

 

 

Таблица 3

Числовые данные к задаче № 3

Номер строки	Номер расч. схемы по	Размер, м	Момент, кН× м	[t], МПа
	рис. 6	а	B	с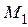
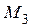
		0,8	0,4	1,0	2,0	1,6	1,0
		0,6	0,5	0,5	1,8	1,7	1,2
		0,4	0,7	0,7	1,7	0,9	0,7
		0,6	0,4	0,6	1,5	0,8	1,5
		0,5	0,8	0,4	1,3	2,0	1,4
		0,7	1,0	0,8	1,0	1,7	2,0
		1,0	0,7	1,0	1,6	1,5	1,6
		0,4	0,6	0,5	1,4	1.6	1,8
		0,7	0,4	0,6	1,5	0,8	0,9
		0,5	0,5	0,4	0,9	1,0	1,5
	з	ж	а	б	в	г	д	е

 

Рис. 6. Расчетные схемы к задаче № 3

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 3

 

Основные теоретические сведения и расчетные формулы

Брус, нагруженный пара­ми­ сил, плоскости действия которых пер­пендикулярны его оси, испытывает де­­фор­мацию кручения. Внутренним сило­вым фактором в по­перечном сечении бруса в этом случае является крутящий момент 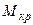, ве­ли­чину которого опре­деляют методом сечений.

На основании этого метода можно сформулировать правило для опреде­ления крутящего момента в сечении бруса: крутящий момент в любом сечении бруса численно равен алгебраической сумме крутящих моментов, распо­ло­жен­ных по одну сторону от этого сечения; при этом крутящий момент, прило­женный к брусу, считается условно поло­жи­тель­ным, если при взгляде вдоль оси бруса с левого конца мы видим его нап­равленным по ходу часовой стрел­ки.

Размеры и форма поперечного сечения бруса в расчетах на кручение учи­ты­ваются двумя геометрическими характеристиками: полярным моментом ине­р­ции 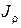и полярным моментом сопротивления 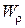. Для круглого сечения они вы­­числяются по следующим формулам:

(3.1)

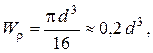(3.2)

где d - диаметр сечения.

Крутящий момент вызывает в сечениях касательные напряжения 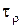, вычисляемых по формуле

, (3.3)

 

где 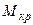- крутящий момент в сечении бруса;

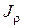- полярный момент инерции сечения;

- расстояние от центра тяжести сечения до точки, в которой опреде­ля­ются напряжения.

Условие прочности записывается в виде

 

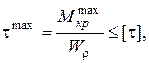(3.4)

где 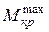- максимальная по модулю величина крутящего момента, определяемого по эпюре ;

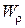- полярный момент сопротивления;

[t] - допускаемое касательное напряжение.

Деформация при кручении характеризуется углом закручивания j(рад):

 

(3.5)

где l - длина бруса;
G - модуль сдвига (модуль упругости второго рода).

Угол закручивания на единице длины бруса называется относительным уг­лом закручивания и вычисляется по формуле

 

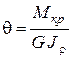. (3.6)

 

Условие жесткости накладывает ограничение на величину отно­си­тель­но­го угла закручивания:

,

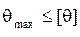где [q] - допускаемый угол закручивания.

Условие жесткости с учетом формулы (3.6) имеет вид

 

. (3.7)

 

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №3

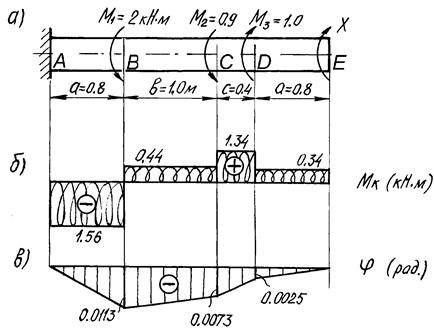Рис. 7. Брус, работающий на кручение: а - расчетная схема; б - эпюра крутящих моментов; в - эпюра углов закручивания

Для заданного бруса круглого сечения (рис. 7, а) определить величину момента X, при котором угол поворота свободного конца бруса равен нулю, по­строить эпюры крутящих моментов и углов закручивания, подобрать ди­аметр сечения по условию прочности и произвести проверку бруса на жесткость.

Числовые данные к задаче: а =0,8 м; в =1,0 м;
с =0,4 м; M₁= 2 кН× м; M₂= 0,9кН×м; [t]=40 МПа; G= 8×10⁴ МПа.

1.Определение величи­ны неизвестного кру­тя­щего момента Х.

Брус жестко заделан левым концом А, правый конец Е свободный. В сечениях В, С, и D при­ложены известные крутя­щие моменты. Для опре­деления неизвестного мо­мента Х используем усло­вие равенства нулю угла поворота сечения Е.

Угол поворота сечения Е относительно сечения А определяется как сумма углов закручивания отдельных участков:

(3.8)

Крутящие моменты , входящие в выражение (3.8), определяются по приведенному выше правилу.

Вычисления начинаем с незакрепленного конца:

 

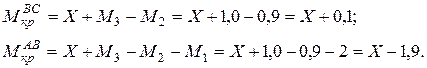(3.9)

Используя выражения (3.9) и сок­ра­щая на 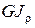, приводим уравнение (3.8) к виду

.

 

Подставляя значения a, b, c (рис. 7, а.) и решая это уравнение, получаем Х = 0,34 кН×м.

Примечание: если значение Х получится со знаком минус, направ­ление кру­тящего момента задано неправильно. В данном примере X положителен, сле­довательно, направление кру­тя­­щего момента, показанное на рис.7, пра­ви­льно.

 

2. Построение эпюры крутящих моментов.

Найденное значение Х = 0,34кН×м подставляем в выражения (3.9), вы­числяя таким образом величину крутящего момента на каждом участке:

По найденным значениям строим эпюру крутящих моментов. Для это­го рассматриваем последовательно участки ЕD, DC, CB и CA. Крутящие мо­менты, действующие на этих участках, уже вычислены.

Величина крутящего момента на каждом участке не зависит от поло­же­ния се­че­ния в пределах участка (крутящий момент постоянен), поэтому эпю­ра кру­тя­щих моментов ограничена отрезками прямых (рис.7,б). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует мак­си­маль­ный (по модулю) крутящий момент.

В рассматриваемом примере опасными будут сечения в пределах учас­т­ка АВ; расчетное значение крутящего момента

 

 

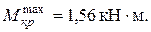
3. Подбор диаметра поперечного сечения бруса.

Используем условие прочности (3.4)

.

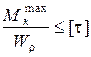Учитывая, что 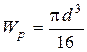, выразим диаметр из условия прочности

 

Подставляя 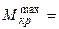1,56 кН×м и , вычисляем диаметр по­пе­речного сечения, округляя его до стандартной величины:

 

 

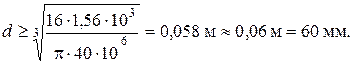
4. Проверка условия жесткости.

Условие жесткости записываем в форме (3.7):

.

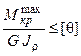По условию задачи [q]= 1 град/м. Переводя значение угла из градусной меры в радианную, получаем

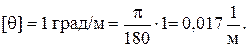
Вычисляем выражение, стоящее в левой части условия жесткости, опре­де­лив предварительно величину полярного момента инерции бруса:

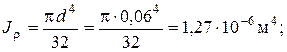
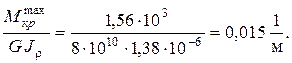
Сравнение левой и правой частей условия жесткости показывает, что оно вы­­по­л­­няется:

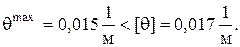
5. Построение эпюры углов закручивания.

Вычисляем углы закручивания по участкам, используя формулу (3.5):

 

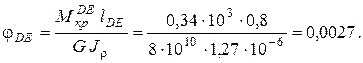
Угол поворота каждого сечения равен сумме углов закручивания соот­ветствующих участков бруса. Суммирование углов начинаем с незакрепленного кон­ца А:

 

так как сечение в заделке неподвижно;

 

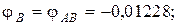
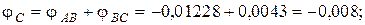
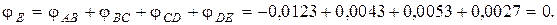
По вычисленным углам поворота сечений построена эпюра углов закру­чи­вания (рис. 7, в).

Равенство является проверкой решения, так как неизвестный кру­тя­щий момент Х определялся из условия равенства нулю угла поворота сво­бод­ного конца бруса.