Упругие свойства твердых тел

Важнейшие положения теории упругости широко используются для проведения расчетов при конструировании машин и агрегатов. Для практических целей необходимо знать константы упру­гости, характеризующие тот или иной материал. Наряду с этим точное измерение этих материальных констант позволяет физику и металловеду судить о межатомном взаимодействии и о фазовых превращениях вещества. Упругость, так же как и другие физи­ческие свойства, может быть использована для исследования ме­таллов и сплавов и решения задач металловедения.

Основными величинами, характеризующими упругость, яв­ляются:

Е — модуль нормальной упругости (модуль Юнга);

G — модуль сдвига;

D — модуль всестороннего сжатия (или объемной упругости);

μ — коэффициент Пуассона.

Эти четыре величины связаны между собой двумя соотно­шениями:

, (1.11)

и

. (1.12)

Три указанные модуля (, , ) характеризуют пропорцио­нальность между напряжением и упругой деформацией соответ­ственно при растяжении, сдвиге и всестороннем сжатии. Это яв­ляется следствием элементарного закона Гука для деформаций в упругой области

, , , (1.13)

где s, t и р — напряжение: нормальное, касательное и всесторон­него сжатия; ε, g, ∆V/V — относительное растяжение, сдвиг и изменение объема.

Здесь предполагается, что напряжение и деформация совпа­дают по направлению.

Коэффициент Пуассона характеризует изменение объема тела при упругой деформации: увеличение при растяжении и уменьшение при сжатии. Например, при одностороннем растяже­нии увеличение объема тела вследствие его удлинения только частично компенсируется поперечным сужением. Аналогичное яв­ление происходит при одностороннем сжатии.

, (1.14)

где и — относительное изменение поперечных и продоль­ных размеров тела призматической формы. Величина одинакова при растяжении и сжатии.

Рисунок 1.4 - Отношение модуля сдвига к модулю Юнга при 0 К для металлов с решеткой о. ц. к., г. ц. к. и г. п. Прямая линия соответствует отношению (=0,375).

Для большинства металлов и сплавов находится в пределах от 0,25 до 0,35; наименьшее найдено у Be (0,039), наибольшее — у РЬ (0,44), Тl и In (0,46).

Ввиду близости значений коэффициента Пуассона у метал­лов отношение модуля сдвига к модулю нормальной упругости для большинства металлов должно быть близким (см. формулу (1.11)). Из экспериментальных данных следует, что . Насколько хорошо это выражение соответствует экспериментальным данным, показывает рисунок 1.4, на котором указано отношение при 0 К для о. ц. к., г. ц. к. и гексагональных металлов. Для кубических металлов более хорошее согласие с экспериментальными значе­ниями дает отношение .

Приведенное описание и относится к одноосной деформа­ции тела. Для полного описания закона Гука следует рассмотреть соотношения между приложенными силами и деформациями кри­сталла при произвольной (сложной) деформации. Для этого в декартовой системе координат нужно найти компоненты дефор­мации и напряжения, а тем самым и компоненты модуля упру­гости тела. Последние полезно знать для того, чтобы оценить анизотропию упругости в кристалле. Рассмотрим упругую де­формацию куба (рисунок 1.5), при которой исключено его чистое вра­щение вокруг какой-либо точки. В отсутствии вращения будут уравновешены все действующие на куб силы. На рисунке 1.5 пока­заны все возможные силы (X, Y, Z), приложенные вдоль осей х, у и z. Если принять площадь каждой грани куба равной 1 см², то эти силы равны приложенным напряжениям:

 

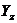
Рисунок 1.5 - Компоненты напряжений в декартовой системе координат.

Диагональные величины , и — это растягивающие или сжимающие, в зависимости от знака «+» или «-», напряжения (нормальные напряжения), так как они перпендикулярны гра­ням куба. Другие шесть величин — это касательные напря­жения, направленные парал­лельно граням куба. Нетрудно видеть, что эти напряжения попарно равны:

Первая пара направлена параллельно плоскости ух, вторая уz, третья хz. Таким образом, равновесие определяется шестью напряжениями: тремя нормальными и тремя касательными. Их обозначают:

и называют компонентами напряжения.

Аналогично этому и деформация тела, когда оно деформиро­вано без чистого вращения, может быть описана шестью компо­нентами, а именно:

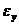
Величины 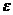характеризуют удлинение (сжатие) вдоль каждой из координат, а — сдвиг по каждой из трех плоскостей куба ху, уz и zх.

Закон Гука заключается в том, что компоненты напряжения являются линейной функцией компонент упругой деформации.

В уравнениях (1.13) приведены такие функции для усредненных по всему объему характеристик деформации и напряжения. Если закон Гука выписать в полном виде по всем компонентам, то нужно составить следующие шесть уравнений:

, (1.15)

, (1.16)

Коэффициенты (i = 1, 2, 3, 4, 5, 6 и j = 1, 2, 3, 4, 5, 6) называют модулями упругости. Как видно, для полного описа­ния упругого поведения тела нужно определить 36 материальных констант . Однако в ряде случаев число коэффициентов неве­лико, так как многие из них либо равны нулю, либо взаимно связаны простыми уравнениями. Например, для квазиизотроп­ного металла (мелкокристаллического и нетекстурованного) до­статочно двух коэффициентов — Е (удлинение) и G (сдвиг), фи­гурирующих в уравнениях (1.11) и (1.12). Для кубических кристал­лов (Аl, Аu, Сu, Pb, Fe, Na, W) достаточно трех коэффициен­тов — 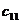, , 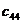— для полного описания упругой деформации.

Для кристаллов с гексагональной решеткой (Mg, Zn, Cd) достаточно знать пять констант (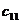, , , , 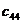), для металлов с низшей симметрией (Sb, Bi, Sn) шесть констант — пять выше­указанных и . В случае кубических кристаллов 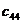характе­ризует сопротивление сдвигу в плоскости куба вдоль ребра куба; величина ½ определяет сопротивление сдвигу в плоскости 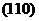вдоль направления . Отношение характери-зует анизотропное сопротивление кристал­лической решетки воздействию внешних сдвигающих напряжений и называется показателем анизотропии. Для изотропного тела . Среди металлов лишь W упруго изотропен при комнатной температуре. Для металлов показатель анизотропии находится в пределах ; щелочные металлы имеют особенно силь­ную анизотропию: для калия 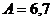, для лития . Для большинства кубических металлов показатель анизотропии : .

Из числа кубических металлов лишь хром, ванадий и молибден имеют показатель анизотропии меньше единицы; соответственно у этих металлов модуль Е максимален вдоль ребра куба и минимален вдоль пространственной диагонали о. ц. к. ячейки.

Анизотропией упругих свойств характеризуются не только монокристаллы, но во многих случаях также поликристалли­ческие текстурованные материалы. В случае острой текстуры анизотропия упругости приближается к анизотропии монокристалла. В качестве острой текстуры укажем текстуру Госса в Fe—Si электротехнической стали.

Согласно Фойгту, модуль сдвига изотропного поликристалли­ческого металла при постоянной деформации в зернах рассчитывают по формуле

, (1.17)

Значение — это верхний предел. Нижний предел дает формула Ройсса в приближении постоянства напряжений в зернах:

, (1.18)

где для кубических кристаллов

, ,

Модуль упругости Е текстурованного материала в первом приближении может быть найден по правилу аддитивности. В меди, деформированной прессованием через очко, присутствуют в основном две компоненты аксиальной текстуры и . Доли остальных ориентировок в деформированной меди незна­чительны. Поэтому модуль упругости Е вдоль оси прутка равен

, (1.19)

где , — средние доли ориентировок вдоль оси об­разца; , 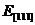— модули Юнга в направлениях и .

Выражение (1.19) может быть использовано для решения часто встречающейся в металловедении задачи нахождения объемных долей компонент кристаллической текстуры, если лишь две компоненты текстуры сильно развиты и известны компоненты модуля упругости монокристалла.

В рамках атомистических представлений упругая деформация означает небольшие обратимые смещения атомов из положений равновесия.

Модули упругости характеризуют силы взаимодействия между соседними атомами в кристаллической решетке и соответственно электронные конфигурации, влияющие на эти силы. Средняя энергия межатомного взаимодействия изменяется с температурой, поэтому модули упругости также зависят от температуры. В тео­рии теплоемкости Дебая (кристаллическое тело paccматривается как изотропный упругий континуум, совершающий гармонические колебания. Температурная зависимость средней энергии гармонического осциллятора определяет температурную зависимость модулей упругости. Поэтому термический коэффициент модулей упругости е изменяется с температурой так же, как теплоемкость 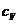, а именно:

е пропорционально при ,

е пропорционально при , (1.20)

При увеличении температуры модуль упругости уменьшается:

, (1.21)

Из соотношений (1.20) и (1.21) следует, что при низких темпе­ратурах модуль упругости изменяется пропорционально , а при высоких температурах () — пропорци­онально .

Однотипная зависимость от температуры величины е и терми­ческого коэффициента расширения α приводит к постоянству их отношения. Согласно эмпирическому уравнению Портевена

, (1.22)

где — абсолютная температура плавления; — удельный объем; , , — константы (, ). Дифференцирование уравнения (1.22) по Т приводит к тому, что пропор­ционально линейному коэффициенту расширения α. Отношение приблизительно равно . В области температур выше наблюдается отклонение температурной зависимости мо­дулей упругости от линейной. Это отклонение (дефект модуля, ) экспоненциально зависит от температуры

, (1.23)

где — энергия активации дефекта модуля, близкая по вели­чине к энергии активации образования вакансий. При нагре­вании от низких температур до плавления модули упругости металлов уменьшаются на 20—30%.

В таблице 1.1 приведены значения термических коэффициентов модулей упругости некоторых поликристаллических и монокри­сталлических металлов в интервале температур 0° С — 0,5 .

 

Таблица 1.1

Экпериментальные величины термических коэффициентов модулей упругости металлов ,

Металл
Ag	Au	Cu	Cr	Fe	Mo	Nb	Pt	Ta	γ-U	V	W

 

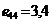
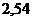
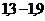
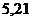
Из таблицы 1.1 видно, что тугоплавкие металлы имеют наиболее низкие термические коэффициенты модулей упругости. Темпера­тура плавления, так же как и модули упругости, характеризует силы связи в металлах. Поэтому между изотропными (поликри­сталлическими) модулями упругости Е, G, D большинства метал­лов и металлоподобных карбидов (ZrC, NbC, WC, TaC, HfC и др.) и отношением имеет место простая линейная зависимость.

Термические коэффициенты модулей упругости Е и G монокристаллов и поликристаллических материалов зависят от кристаллографического направления: они максимальны в направле­ниях, соответствующих минимуму модулей упругости и, напротив, минимальны в направлениях, где модули упругости достигают максимума.

Модули упругости, равно как температура Дебая, заметно возрастают при увеличении давления Р. Модуль объемной упругости равен обратной величине коэффициента всестороннею сжатия:

, (1.24)

Зависимость D от давления может быть представлена в виде:

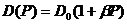, (1.25)

где барический коэффициент модуля

, (1.26)

Для Fe этот коэффициент равен , для Cu

для Ag .

Монотонный ход температурной зависимости модулей упру­гости прерывается в точках фазовых переходов (установление ферромагнитного или антиферромагнитного порядка, аллотропи­ческие превращения и т. п.). Было исследовано влияние тем­пературы на модули сдвига и показатель анизотропии α -Fe. При температурах от 0 до 700° С 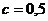(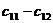), модуль сдвига 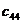и показатель анизотропии А изменяются линейно, вблизи точки Кюри на кривых температурной зависимости мо­дулей и А наблюдаются перегибы. При низких температурах наклон кривых уменьшается в соответствии с выражением (1.20). Рисунок 1.6 Периодическое изменение модуля нормальной упру­гости

и модули стремятся к постоянной величине. Увеличение модуля сдвига, а также модуля упругости Е железа при переходе в ферро­магнитное состояние соответствует уменьшению коэффициента термического расширения, -превращение железа повышает Е в связи с увеличением компактности решетки.

Под влиянием наклепа объемноцентрированного α -железа зна­чение Е уменьшается. У металлов с гранецентрированной куби­ческой решеткой (Al, Ni и Сu) также наблюдается падение модуля нормальной упругости при наклепе, которое при сильных степенях деформации сменяется увеличением. Последнее объясняется тек­стурой протяжки .

Модуль упругости при комнатной температуре является пе­риодической функцией атомного номера элемента (рисунок 1.6).

Среди элементов третьего периода — Na, Mg, Al и Si, модуль увеличивается вместе с атомным номером, что связано с увеличе­нием числа валентных электронов и уменьшением атомного радиуса. Среди элементов одной группы, например Be, Mg, Ca, Sr и Ва, с увеличением атомного номера модуль упругости умень­шается наряду с увеличением атомного радиуса.

Модуль упругости переходных металлов относительно высок, что можно приписать значительной силе межатомной связи, обусловленной d-электронами. Наибольшее значение модуля имеют элементы с 5—7 d -электронами (Os, Ru, Fe, Mo, Co и др.).