Упругая и пластическая деформации твердых тел

Глава 1 Механические свойства твердых тел

При действии на кристалл внешней растягивающей нагрузки рас­стояние между атомами увеличивается и равновесное расположение их в кристалле нарушается. Это приводит к нарушению равенства сил притяжения и отталкивания, характерного для равновесного состоя­ния атомов в решетке, и возникновению внутренних сил, стремящихся вернуть атомы в первоначальные положения равновесия. Величину этих сил, рассчитанную на единицу площади поперечного сечения кри­сталла, называют напряжением. Вычислим его.

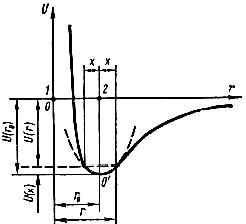
Энергия взаимодействия частиц 1 и 2 в твердом теле является функцией расстояния между ними и опи­сывается кривой , схематически показанной на рисунке 1.1, а. При смещении частицы 2 из положения равновесия на расстояние , т. е. при увеличении расстояния между частицами до , энергия частицы увеличивается, становясь равной . Изменение энергии можно найти, разлагая в ряд Тейлора по степеням :

(1.1)

Ограничиваясь квадратичным членом разложения и учитывая, что в точке О' равна нулю, находим

, (1.2)

где — жесткость связи.

Мы получили приближенное выражение для изменения энергии частицы вследствие смещения ее из положения равновесия на расстоя­ние . Приближенным оно яв­ляется потому, что в разложении (1.1) мы ограничились квадра­тичным членом и отбросили чле­ны более высокого порядка.

Графически зависимость в таком приближении выражается пара­болой, показанной на рисунке 1.1, а пунктиром.

а) б)

Рисунок 1.1 – Изменения энергии частицы вследствие смещения ее из положения равновесия на расстояние x.

Сила, которая возникает меж­ду частицами 1 и 2 при измене­нии расстояния между ними на , равна

. (1.3)

Как видно из (1.3), сила пропорциональна первой степени смещения и направлена к положению равновесия, на что указывает знак минус. Известно, что под действием такой силы тело совершает гармоничес­кие колебания. Поэтому такую силу называют гармонической, а при­ближение (1.2), приведшее к гармонической силе, называют гармони­ческим приближением. На рисунке 1.1, б показан схематический график зависимости в области малых значений ; он представляет собой прямую линию.

Теперь представим себе, что к стержню с поперечным сечением и длиной приложена растягивающая сила , которая изменяет рас­стояние между соседними атомными плоскостями 1 и 2 на , вызывая тем самым удлинение стержня на 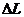(рисунок 1.2). Эта сила будет уравно­вешена внутренней силой , численно равной

, (1.4)

где — число частиц, находящихся в атомном слое площадью . Напряжения , которые возникнут в растянутом стержне, будут равны

, (1.5)

где . Умножая и деля правую часть (1.5) на расстояние меж­ду атомными плоскостями , получим

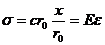, (1.6)

где

, (1.7)

называется модулем упругости, или модулем Юнга, а

, (1.8)

представляет собой относительное изменение параметра решетки в на­правлении действия внешней силы .

Рисунок 1.2 Изменение рас­стояния между соседними атомными плоскостями 1 и 2 на

Умножая числитель и знаменатель выражения (1.8) на число атом­ных слоев , размещающихся на длине образца , найдем

, (1.9)

Таким образом, 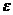представляет собой относительное удлинение образ­ца, вызванное действием внешней растягивающей силы.

Из формулы (1.6) видно, что до тех пор, пока выполняется гармо­ническое приближение, т. е. пока силы, возникающие при смещении частиц относительно друг друга вследствие деформации тела, остаются линейными функциями смещения, напряжения , формирующиеся в теле, будут пропорциональны относительной деформации тела:

, (1.10)

Коэффициентом пропорциональности служит модуль упругости .

Формула (1.6) выражает известный закон Гука. Как видим, он справедлив лишь постольку, поскольку справедливо гармоническое приближение, т. е. для очень малых относительных деформаций .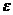

Из формулы (1.6) легко установить физический смысл модуля упру­гости. Положив 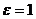, находим . Следовательно, модуль упругости численно равен напряжению, которое способно было бы вызвать растяжение образца на , если бы при этом закон Гука не нарушался и образец не разрушался. Ни один реальный материал, кроме резины, таких деформаций не выдерживает.

Модуль упругости твердых тел имеет весьма высокое значение (порядка Па), что свидетельствует о том, что в этих телах силы связи очень велики.

Для ряда кристаллов модуль упругости существенно зависит от направления, в котором происходит деформация решетки. Отношение для некоторых кристаллов достигает 3, что указывает на высокую анизотропию таких кристаллов.

Модуль упругости зависит только от природы атомов (молекул), образующих тело, и от их взаимного расположения. Изменить его можно лишь путем значительного изменения состава или внутренней структуры твердого тела. Однако и в этом случае наблюдается лишь срав­нительно небольшое изменение . Так, введение в сталь значительных количеств легирующих добавок, термическая обработка, холодная прокатка и т. д. сильно увеличивают ее твердость и другие механичес­кие характеристики и лишь незначительно изменяют (до 10 %) модуль упругости; введение в медь до 40% цинка не меняет практически модуль упругости, хотя другие свойства меняются при этом очень сильно. Мы рассмотрели деформацию растяжения. Однако все рассуждения и полученные результаты остаются справедливыми и для других видов деформации — сжатия и сдвига. В последнем случае следует брать вместо модуля упругости модуль сдвига .

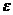При непрерывном увеличении внешней нагрузки непрерывно растут напряжение и деформация (рисунок 1.3). При некотором напряжении , характерном для каждого материала, наблюдается или разрушение кристалла, или нарушение прямой пропорциональности между и 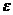и возникновение остаточной (пластической) деформации , не исчезающей после снятия внешней нагрузки. В первом случае материал является хрупким, во втором — пластичным. Напряжение , при котором начинается заметное течение тела, называется пределом текучести области и — соответственно областями упругой и пласти­ческой деформации.

Рисунок 1.3 Непрерывный рост напряжения и деформации .

В хрупких материалах предел упругости совпадает с пределом проч­ности, поэтому они разрушаются без видимой пластической деформа­ции. В пластичных же металлах предел упругости и текучести, как правило, значительно меньше предела прочности. Поэтому разрушение таких материалов происходит после значительной пластической деформации.