Пусть задана функция  . Если для любого
. Если для любого  несобственный интеграл
несобственный интеграл  с особой точкой
с особой точкой  сходится, то определена функция
сходится, то определена функция 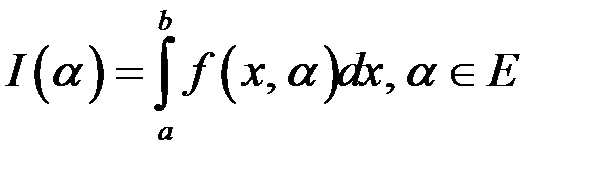 .
.
Теоремы, справедливые для собственных интегралов, зависящих от параметра, могут быть несправедливыми для несобственных интегралов.
Пример 1. Рассмотрим при 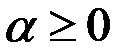 интеграл
интеграл

Подынтегральная функция непрерывна на множестве  . а функция
. а функция  терпит разрыв в точке
терпит разрыв в точке 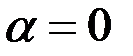 .
.
Для того, чтобы обобщить теоремы, справедливые для собственных интегралов, зависящих от параметра, на несобственные интегралы вводится понятие равномерной сходимости по параметру несобственного интеграла.
Если у несобственного интеграла две особых точки, то нужно такой интеграл представить в виде суммы двух интегралов с одной особой точкой и исследовать каждый интеграл на равномерную сходимость. Без ограничения общности можно ограничиться рассмотрением интегралов с особой точкой  .
.
Определение. Пусть несобственный интеграл  сходится при всех
сходится при всех  . Будем говорить, что
. Будем говорить, что  сходится на множестве
сходится на множестве  равномерно по параметру
равномерно по параметру 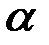 , если
, если  при
при  .
.
Замечание. Из определения следует, что интеграл

сходится равномерно по параметру на множестве  в том и только в том случае, когда для любого числа
в том и только в том случае, когда для любого числа  интеграл
интеграл

сходится равномерно.
Пример 1. C3. §14 1(1,2)
Исследовать интеграл на равномерную сходимость
1)  на множествах
на множествах  и
и 
Решение. При 

 при
при  .
.
Так как
 то
то  при
при  .
.
Интеграл сходится равномерно на множестве 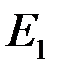 .
.
Если  , то
, то

 не стремится к нулю при
не стремится к нулю при  . Интеграл сходится неравномерно на множестве
. Интеграл сходится неравномерно на множестве  .
.
Пример 2.. C3. §14 6(4)
Интеграл  сходится равномерно на множестве
сходится равномерно на множестве  и сходится неравномерно на множестве
и сходится неравномерно на множестве 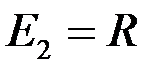 .
.
Если  , то
, то
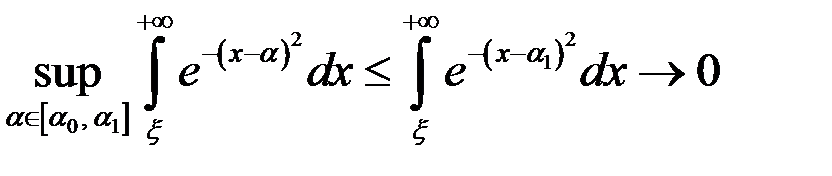 при
при  .
.
Если 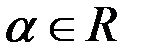 , то
, то

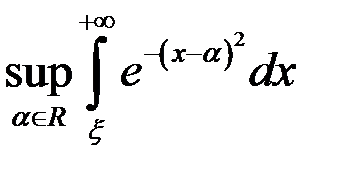 не стремится к нулю при
не стремится к нулю при  . Интеграл сходится неравномерно на множестве
. Интеграл сходится неравномерно на множестве 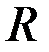 .
.
Пример 3. С. §14. 7(6)

Решение. Если 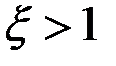 , то
, то

 не стремится к нулю при
не стремится к нулю при 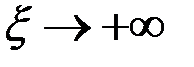 . Интеграл сходится неравномерно по параметру на множестве
. Интеграл сходится неравномерно по параметру на множестве 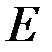 .
.
Критерий Коши равномерной сходимости несобственного интеграла.
Для того, чтобы несобственный интеграл  с особой точкой
с особой точкой  сходился равномерно по параметру
сходился равномерно по параметру  на множестве
на множестве  необходимо, чтобы выполнялось следующее условие Коши: для любого
необходимо, чтобы выполнялось следующее условие Коши: для любого  найдется такое число
найдется такое число  , что для любых двух чисел
, что для любых двух чисел  выполнено неравенство
выполнено неравенство
 .
.
Замечание. Несобственный интеграл  с особой точкой
с особой точкой  сходился неравномерно по параметру
сходился неравномерно по параметру  на множестве, если не выполнено условие Коши. Строим отрицание: условие Коши не выполнено, если найдется такое число
на множестве, если не выполнено условие Коши. Строим отрицание: условие Коши не выполнено, если найдется такое число 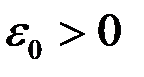 , что для любого
, что для любого 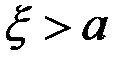 найдутся такие числа
найдутся такие числа  , что
, что  .
.
Достаточные условия равномерной сходимости несобственного интеграла.
Теорема. (признак Вейерштрасса равномерно сходимости несобственного интеграла). Еслиb 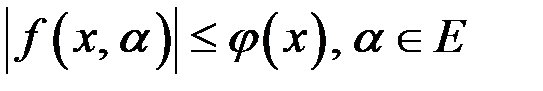 и
и  , то несобственный интеграл
, то несобственный интеграл  сходится равномерно по параметру на множестве
сходится равномерно по параметру на множестве  .
.
Доказательство.
 ,
,
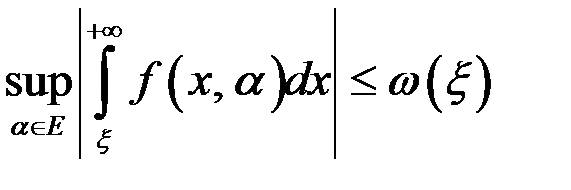
Так как интеграл  сходится, то
сходится, то  при
при  . Следовательно,
. Следовательно,
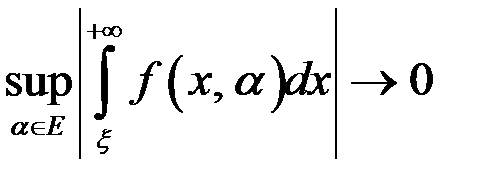 при
при  . Интеграл
. Интеграл  сходится равномерно по параметру на множестве
сходится равномерно по параметру на множестве  .
.
Пример 4. Интеграл  сходится равномерно по параметру
сходится равномерно по параметру  на множестве
на множестве  .
.
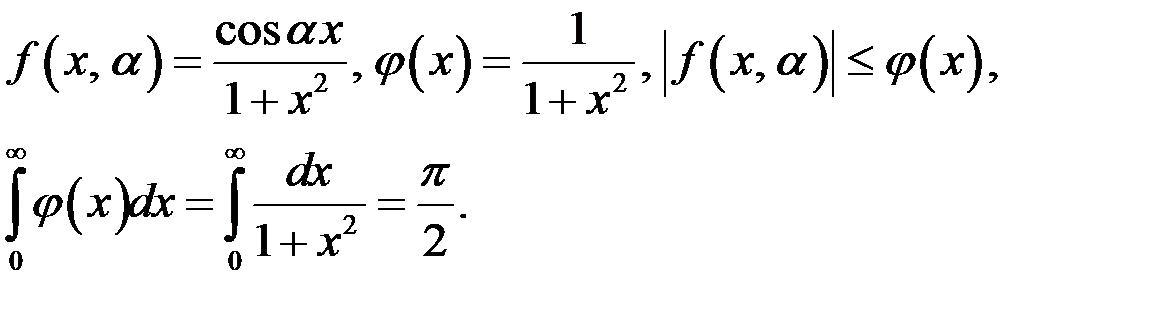
Так как  сходится, то по признаку Вейерштрасса
сходится, то по признаку Вейерштрасса  сходится равномерно по параметру на множестве
сходится равномерно по параметру на множестве
 .
.
Пример 5. Пусть  . Интеграл
. Интеграл  сходится равномерно на множестве
сходится равномерно на множестве  и сходится неравномерно на множестве
и сходится неравномерно на множестве  .
.
Решение. Пусть  . Если
. Если  , то
, то
 ,
,
В силу признака Вейерштрасса интеграл 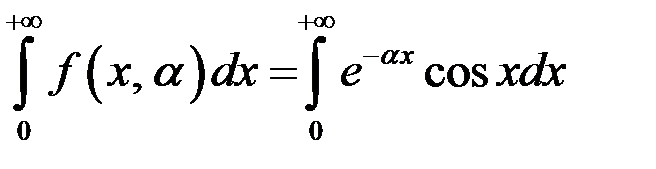 сходится равномерно по параметру
сходится равномерно по параметру  на множестве
на множестве  .
.
Покажем, что условие Коши не выполнено на множестве  . Пусть задано произвольное число
. Пусть задано произвольное число  . Найдется такое натуральное число
. Найдется такое натуральное число  , что
, что  . Положим
. Положим
 . На отрезке
. На отрезке  выполнено неравенство
выполнено неравенство
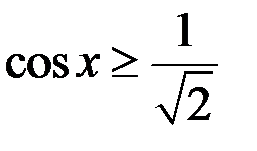 . Но тогда,
. Но тогда,

Условие Коши не выполнено интеграл сходится неравномерно по параметру на множестве 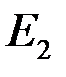 .
.
Рассмотрим несобственный интеграл  с особой точкой
с особой точкой 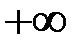 .
.
Теорема. (Признак Дирихле равномерно сходимости интеграла по параметру).
Если при  выполнены следующие условия
выполнены следующие условия
1) непрерывная функция  имеет по переменной
имеет по переменной  первообразную
первообразную  и
и  ,
,
2) функция  и частная производная
и частная производная  являются непрерывными функциями переменной
являются непрерывными функциями переменной  .
.
3) При любом 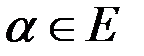 Функция
Функция  монотонна по переменной
монотонна по переменной  и равномерно по параметру стремится к нулю при
и равномерно по параметру стремится к нулю при  ,
,
то интеграл  сходится равномерно по параметру на множестве
сходится равномерно по параметру на множестве  .
.
Доказательство. Применим формулу интегрирования по частям
 (1)
(1)
При любом значении параметра функция  монотонна. Без ограничения общности можно считать, что она убывает. Следовательно,
монотонна. Без ограничения общности можно считать, что она убывает. Следовательно,  . Так как
. Так как  равномерно по параметру стремится к нулю при
равномерно по параметру стремится к нулю при  , то
, то  при
при  . Из равенства (1) получаем, что
. Из равенства (1) получаем, что

Следовательно,
 при
при  .
.
Интеграл  сходится равномерно по параметру на множестве
сходится равномерно по параметру на множестве  .
.
Аналогично формулируются признаки равномерной сходимости для интегралов с конечной особой точкой.
Доказательство следующих двух теорем можно найти в любом рекомендуемом учебнике.
Теорема 1. (о непрерывной зависимости несобственного интеграла от параметра и интегрируемости интеграла по параметру). Если функция  непрерывна на множестве
непрерывна на множестве 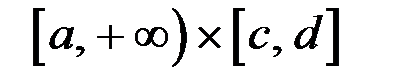 и интеграл
и интеграл  с особой точкой
с особой точкой  сходится равномерно на отрезке
сходится равномерно на отрезке  , то интеграл
, то интеграл  является непрерывной функцией параметра на отрезке
является непрерывной функцией параметра на отрезке  и справедлива формула перемены порядка интегрирования
и справедлива формула перемены порядка интегрирования
 . (1)
. (1)
Теорема 2. (о дифференцируемости несобственного интеграла по параметру). Если функции  и
и  непрерывны на множестве
непрерывны на множестве 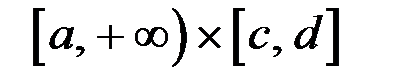 , интеграл
, интеграл  с особой точкой
с особой точкой 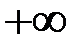 сходится и интеграл
сходится и интеграл  сходится равномерно на отрезке
сходится равномерно на отрезке  , то интеграл
, то интеграл  является непрерывно дифференцируемой функцией параметра на отрезке
является непрерывно дифференцируемой функцией параметра на отрезке  и
и
 . (2)
. (2)
Теоремы 1 и 2 являются эффективным инструментом при вычислении многих несобственных интегралов.
Пример 6. Вычисление интеграла Дирихле 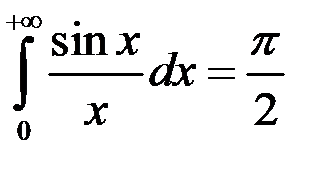 .
.
Решение. Рассмотрим интеграл
 , (3)
, (3)
Покажем, что этот интеграл сходится равномерно не множестве  . Функция
. Функция 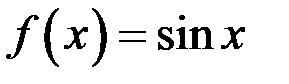 имеет ограниченную первообразную
имеет ограниченную первообразную  , функция
, функция  непрерывно дифференцируема на
непрерывно дифференцируема на  , убывает и равномерно стремится к нулю при
, убывает и равномерно стремится к нулю при  , так как
, так как 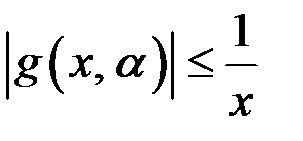 . В силу признака Дирихле интеграл
. В силу признака Дирихле интеграл  сходится равномерно на множестве
сходится равномерно на множестве  . Из теоремы 1 следует, что функция
. Из теоремы 1 следует, что функция  непрерывна на любом отрезке
непрерывна на любом отрезке  . В частности, эта функция непрерывна справа в точке
. В частности, эта функция непрерывна справа в точке 
 . (4)
. (4)
Пусть задан произвольный отрезок  Продифференцируем интеграл (3) по параметру
Продифференцируем интеграл (3) по параметру
 . (5)
. (5)
Так как
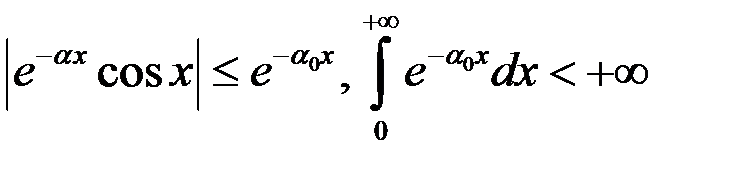 , то по признаку Вейерштрасса интеграл (5) сходится равномерно по параметру на отрезке
, то по признаку Вейерштрасса интеграл (5) сходится равномерно по параметру на отрезке  . Из теоремы 2 следует, что дифференцирование по параметру законно. Интеграл (5) легко вычисляется
. Из теоремы 2 следует, что дифференцирование по параметру законно. Интеграл (5) легко вычисляется
 .
.
Следовательно,
 .
.
Так как  произвольный отрезок, принадлежащий интервалу
произвольный отрезок, принадлежащий интервалу  , то
, то
 (6)
(6)
Так как
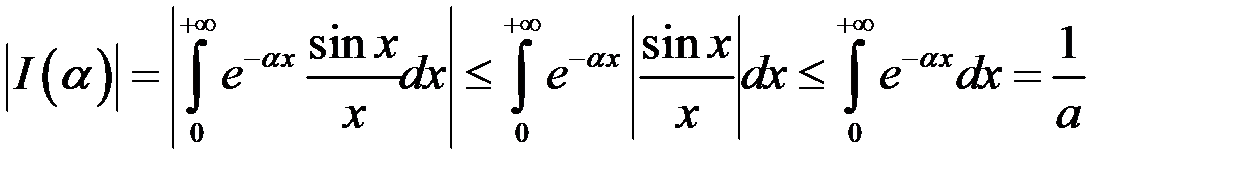 ,
,
то 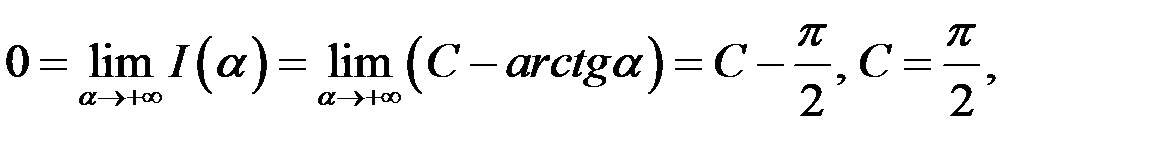
Из равенства (6) следует, что
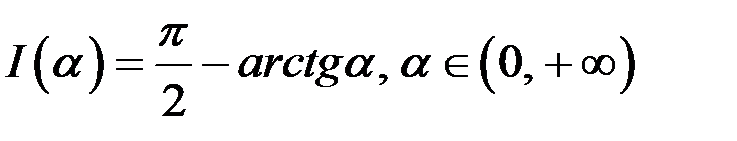 . (7)
. (7)
Из равенства (4) имеем, что

Рассмотрим интеграл, который называют разрывным множителем Дирихле
 . (8)
. (8)
Так как
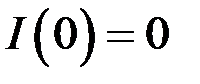 ,
,  , то (9)
, то (9)
достаточно рассмотреть тот случай, когда 
Но при  справедливо равенство
справедливо равенство
 . (10)
. (10)
Из равенств (9) и (10) следует равенство (8).
Пример 7. Вычисление интегралов Лапласа

Так как  , то по признаку Вейерштрасса интеграл
, то по признаку Вейерштрасса интеграл  сходится равномерно по параметру на
сходится равномерно по параметру на  и, поэтому является непрерывной функцией параметра. В частности
и, поэтому является непрерывной функцией параметра. В частности
 .(11)
.(11)
Возьмем произвольное число  . Покажем, что по признаку Дирихле интеграл
. Покажем, что по признаку Дирихле интеграл  равномерно сходится при
равномерно сходится при  : функция
: функция  имеет равномерно ограниченную первообразную
имеет равномерно ограниченную первообразную
 , (12)
, (12)
функция  стремится к нулю при
стремится к нулю при  и имеет производную
и имеет производную  , принимающую отрицательные значения при
, принимающую отрицательные значения при  . Следовательно, функция
. Следовательно, функция 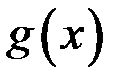 убывает при
убывает при  .
.
Дифференцируя интеграл 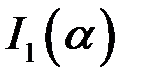 получаем, что
получаем, что

Дифференцирование по параметру законно, так как интеграл  равномерно сходится при
равномерно сходится при  .
.
Если формально продифференцировать  , используя формулу (2), то мы получим расходящийся интеграл. Чтобы обойти это затруднение воспользуемся тем, что при
, используя формулу (2), то мы получим расходящийся интеграл. Чтобы обойти это затруднение воспользуемся тем, что при  интеграл
интеграл  и тем, что
и тем, что
 ,
,
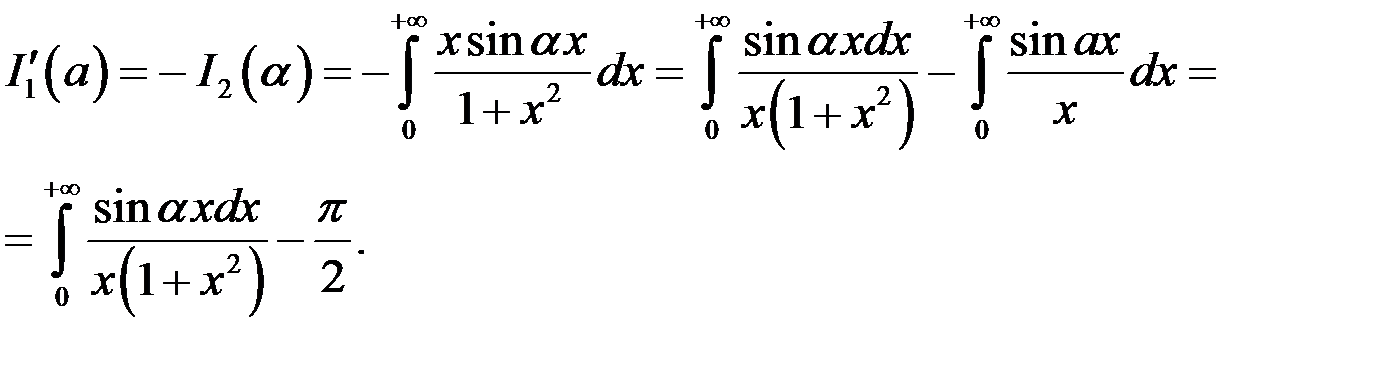
Дифференцируя это равенство, получаем, что
 . (13)
. (13)
Так как  произвольное положительное число, то равенство (13) справедливо при
произвольное положительное число, то равенство (13) справедливо при  . Решая дифференциальное уравнение (13), получаем, что
. Решая дифференциальное уравнение (13), получаем, что
 . (14)
. (14)
Так как
 , то
, то  ограниченная функция и в формуле (14) следует взять
ограниченная функция и в формуле (14) следует взять 
Итак
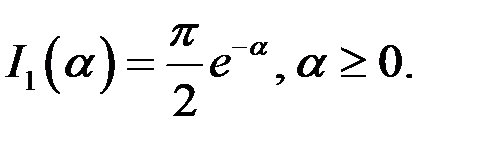
Так как  четная функция, то
четная функция, то
 .
.

Так как  нечетная функция, то
нечетная функция, то
 .
.