Решение задач линейного программирования

Г О С К О М В У З

ДОНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ СЕРВИСА

(ДГАС)

ЛАБОРАТОРНЫЕ РАБОТЫ№ 1, 2

“ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ”

Часть II

<< ИО 1.2 >>

Предназначены для студентов второго

Курса всех специальностей

ШАХТЫ

СОСТАВИТЕЛИ

Доцент кафедры математики ДГАС,

Кандидат физико–математических наук Мальцев И.М.

Ассистент кафедры математики ДГАС Лыткина С.С.

РЕЦЕНЗЕНТЫ

Доцент кафедры математического анализа РГУ,

Кандидат физико–математических наук Мелихов С.Н.

Доцент кафедры математики ДГАС,

Кандидат физико–математических наук Шрайфель И.С.

Методические указания предназначены для выполнения практических и лабораторных работ по разделам “Математическое программирование” и “Экономико-математические методы и модели”. Они содержат теоретическую часть, примеры построения моделей, индивидуальные задания, контрольные вопросы и описание компьютерных программ, входящих в пакет лабораторного практикума “MATH_LAB” кафедры математики ДГАС и предназначенных для решения задач линейного программирования симплекс-методом и модифицированным симплекс-методом. Изложены основы теории двойственности и анализа моделей на чувствительность.

СОДЕРЖАНИЕ

Часть I

Введение
1.	Теоретическая часть
	1.1.	Постановка задач линейного программирования
	1.2.	Преобразование задачи линейного программирования к стандартной форме
	1.3.	Основы симплекс-метода
	1.3.1.	Метод искусственных переменных
	1.3.2.	Двухэтапный симплекс-метод
	1.3.3.	Переход к новому допустимому решению
	1.3.4.	Задачи минимизации
	1.3.5.	Особые случаи применения симплекс-метода
	1.3.6.	Разновидности симплекс-таблиц
	1.4.	Модифицированный симплекс-метод
	1.5.	Описание учебной программы решения общей задачи линейного программирования модифицированным симплекс-методом
	1.6.	Особенности работы с коммерческими пакетами
	1.6.1.	Хранение
	1.6.2.	Ошибки округления
	1.6.3.	Контроль роста ошибок
	1.6.4.	Допуски на ошибку
Список использованных и рекомендуемых источников

Часть II

	1.7.	Двойственность и анализ моделей на чувствительность
2.	Описание программ
3.	Лабораторная работа №1. Решение задач линейного программирования геометрическим методом
	3.1.	Цель работы
	3.2.	Задание
	3.3.	Содержание отчета
	3.4.	Пример выполнения работы
4.	Лабораторная работа №2. Решение задач линейного программирования симплекс-методом и модифицированным симплекс-методом
	4.1.	Цель работы
	4.2.	Задание
	4.3.	Содержание отчета
	4.4.	Пример выполнения лабораторной работы №2
5.	Расчетные задания для выполнения лабораторной работы №1
6.	Расчетные задания для выполнения лабораторной работы №2
7.	Контрольные вопросы
Список использованных и рекомендуемых источников

ЗАДАЧИ ИССЛЕДОВАHИЯ ОПЕРАЦИЙ

В РАСЧЕТАХ HА ЭВМ

Обдумай стезю для ноги

твоей,

и все пути твои да будут

тверды.

Ветхий завет. Книга притчей Соломоновых.

1.7. Двойственность и анализ моделей на чувствительность. Понятие двойственности в линейном программировании имеет как важное теоретическое, так и большое практическое значение. Соотношения двойственности позволяют проводить эффективный анализ моделей на чувствительность к изменениям исходных данных (цен, запасов ресурсов, технологии производства и т.п.).

Двойственная задача формулируется с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. Чаще всего в литературе по линейному программированию даются формулировки двойственных задач, соответствующих различным формам прямой задачи. Например, если исходная задача имеет вид

то соответствующая ей двойственная задача:

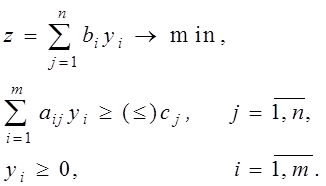
Разнообразие форм задач линейного программирования диктует необходимость универсальных методов построения двойственной задачи. Все эти методы требуют приведения исходной задачи к некоторой стандартной форме.

Допустим, что прямая задача приведена к стандартной форме (см. ч. I, стр. 14-17), которая имеет вид:

Для удобства формулировки правил перехода от прямой к двойственной задаче, расположим коэффициенты, фигурирующие в условиях прямой задачи, в виде таблицы 1. В ней дана схема перехода от прямой задачи к двойственной, которая выражается следующими правилами:

· каждому ограничению прямой задачи соответствует переменная двойственной задачи;

· каждой переменной прямой задачи соответствует ограничение двойственной задачи;

· коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой части этого же ограничения двойственной задачи.

	Переменные прямой задачи
	x₁	x₂	¼	x_j	¼	x_n
Правые части ограничений двойственной задачи	c₁	c₂	¼	c_j	¼	c_n
Коэффициенты левых частей ограничений двойственной задачи	a₁₁ a₂₁ … a_m1	a₁₂ a₂₂ … a_m2	¼ ¼ ¼ ¼	a_1j a_2j … a_mj	¼ ¼ ¼ ¼	a_1n a_2n … a_mn	b₁ b₂ … b_m	y₁ y₂ … y_m	Переменные двойственной задачи

			j-ое ограничение двойственной задачи	Коэффициенты целевой функции двойственной задачи

Таблица 1.

Остальные условия двойственной задачи (направление оптимизации, ограничения и знаки двойственных переменных) формируются в соответствии с таблицей 2.

Прямая задача в	Двойственная задача
стандартной форме Целевая функция	Целевая функция	Ограничения	Переменные
MAX	MIN	³	Не ограничены в знаке
MIN	MAX	£	Не ограничены в знаке

Таблица 2.

Рассмотрим примеры построения двойственных задач.

Пример 1.7.1. Прямая задача:

Прямая задача в стандартной форме:

Двойственная задача:

y₁,y₂ не ограничены в знаке

или, что то же,

y₁,y₂ ³ 0.

В качестве упражнения, проверьте правильность построения двойственных задач.

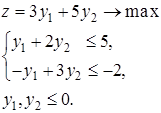
Прямая: Двойственная:

x₁не ограничена в знаке, x₂ ³ 0. y₁ не ограничена в знаке,

y₂ £ 0, y₃ ³ 0.

Связь между прямой и двойственной задачами выражается следующими теоремами.

Теорема 1.7.1. Двойственная задача к двойственной есть прямая задача.

Теорема 1.7.2. Значение максимизируемой (минимизируемой) функции y, соответствующее любому допустимому решению прямой задачи, не больше (не меньше) значения функции z, соответствующего допустимому решению двойственной задачи. В точках, соответствующих оптимальным решениям обеих задач, значения целевых функций прямой и двойственной задач совпадают.

Из этой теоремы следует важный с практической точки зрения вывод: если нам удалось найти какие-либо допустимые решения прямой и двойственной задач с соответствующими значениями целевых функций y₀ и z₀, то оптимальные значения целевых функций обеих задач совпадают и находятся в промежутке между y₀ и z₀. Это можно проиллюстрировать следующей схемой (y ® max, z ® min):

Процессы максимизации и минимизации сходятся к некоторой “точке равновесия” B, после достижения которой целевые функции задач улучшить невозможно. Такая точка достигается при равенстве значений целевых функций обеих задач и соответствует их оптимальным решениям.

Приведем формулировку еще одной теоремы, соответствующей вырожденному случаю.

Теорема 1.7.3. Если целевая функция исходной задачи не ограничена в области допустимых планов, то условия двойственной задачи противоречивы, т.е. область ее допустимых планов пуста.

Оказывается, что оптимальные решения прямой и двойственной задач тесно связаны между собой: зная одно из них, другое можно получить непосредственно из имеющейся оптимальной симплекс-таблицы. Для этого необходимо воспользоваться следующими соотношениями, справедливыми в оптимуме:

· (значение целевой функции прямой задачи) = (значение целевой функции двойственной задачи);

· (коэффициент при начальной базисной переменной в оптимальном y- уравнении прямой задачи) = (левая часть соответствующего ограничения двойственной задачи) - (правая часть соответствующего ограничения двойственной задачи).

Получим, например, решение прямой задачи из примера 1.7.1., воспользовавшись программой MODSM_RV. Оно имеет вид:

11/02/96 11:43:04 MODSM_RV

Zmax = 1.07142857E+01

X[1] = 2.1428571429E+00 Res =–1.455E–11 M[1] = 0.00000000E+00

X[4] = 8.5714285714E–01 Res =–2.728E–12 M[2] = 4.28571429E–01

M[3] = 7.14285714E–01

M[4] = 0.00000000E+00

Надеемся, вы понимаете, что программа выдает в качестве обозначения переменных —X[ i ], а для обозначения целевой функции использует букву Z независимо от того, какую задачу вы решаете и как обозначили свои переменные и целевую функцию (так, в принятых ранее обозначениях, следовало бы записать y_max = 10.7142857). Через M[ i ] здесь обозначены коэффициенты целевой функции в оптимальной симплекс-таблице. Оптимальная симплекс-таблица выводится на монитор перед отображением результатов и может быть либо напечатана на принтере, либо сохранена в текстовом файле:

11/02/96 13:07:15

Заключительная итеpация

B[1;1] = 2.1428571429E+00

B[1;2] = 1.4285714286E-01

B[1;3] = 0.0000000000E+00

B[2;1] = 8.5714285714E-01

B[2;2] =-1.4285714286E-01

B[2;3] = 1.0000000000E+00

B[3;1] = 1.0714285714E+01

B[3;2] = 7.1428571429E-01

B[3;3] = 0.0000000000E+00

Впрочем, в данном случае, для получения оптимального решения двойственной задачи эта таблица не понадобится. Оптимальное значение целевой функции двойственной задачи совпадает с оптимальным значением целевой функции прямой задачи, т.е. z _min= y _max = 10.7142857. Так как в исходной стандартной модели первоначальными базисными переменными являлись x₃ и x₄, то получаем следующую таблицу для отыскания оптимальных значений двойственных переменных (приведенные значения округлены):

Начальные базисные переменные прямой задачи	x₃	x₄
Коэффициенты в оптимальном y- уравнении	0.7142857	0
Разность между левыми и правыми частями соответствующего ограничения двойственной задачи.	y₁ - 0	y₂- 0

Отсюда y₁ = 0.7142857, y₂= 0. Решая двойственную задачу с помощью компьютера, получим:

11/02/96 13:11:24 MODSM_RV

Zmin = 1.07142857E+01

X[4] = 4.2857142857E–01 Res = 0.000E+00 M[1] = 0.00000000E+00

X[1] = 7.1428571429E–01 Res = 0.000E+00 M[2] = 8.57142857E–01

M[3] = 2.14285714E+00

M[4] = 0.00000000E+00

M[5] = 1.00000000E+00

M[6] = 1.00000000E+00

Как видим, результаты совпали. Попробуйте теперь по результатам двойственной задачи восстановить оптимальное решение прямой и, если вас не затруднит, убедитесь, что оптимальным решением задачи двойственной к

является z _min = 54.8, y₁ = 5.8, y₂ = -0.4. При этом вам понадобится информация о том, каким именно образом программа приводит исходную модель к стандартной форме. Ее можно найти, вызвав в программе помощь (нажав клавишу <F1>).

Итак, мы убедились, что для нахождения обоих решений – прямой и двойственной задач – достаточно решить одну из них. При этом лучше решать ту, которая имеет меньшее количество ограничений (трудоемкость решения задачи линейного программирования симплекс-методом в большей мере зависит от количества базисных переменных, чем от их общего количества).

Возможности, предоставляемые теорией ЛП и симплекс-методом, не ограничиваются лишь получением оптимальных значений переменных ЗЛП. Решение задач ЛП должно обеспечивать пользователя динамичной информацией. Как только условия, в соответствии с которыми была построена модель, изменяются, информация, ассоциированная со статическим оптимальным решением, обычно сразу же теряет актуальность. Анализ модели на чувствительность как раз и связан с исследованием возможных изменений полученного оптимального решения в результате изменений исходной модели.

Для тех, кто хочет глубже понять идеи анализа модели на чувствительность, советуем обратиться к методическим указаниям [2], где подробно разобран геометрический смысл этого анализа.

Рассмотрим анализ моделей на чувствительность на примере задачи распределения ограниченных ресурсов с целевой функцией подлежащей максимизации:

Прямая задача: Двойственная задача:

Сначала разберемся с экономическим смыслом параметров, входящих в прямую задачу.

y – прибыль от реализации всей произведенной продукции,

c_j – прибыль, приходящаяся на единицу продукции j- го вида,

x_j – объем производства продукции j- го вида,

a_ij – расход ресурса i, запасы которого ограничены величиной b_i, на единицу продукции j- го вида производственной деятельности.

Учитывая, что в оптимуме значения целевых функций прямой и двойственной задач совпадают, можем записать:

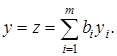
Так как прибыль y выражается в денежных единицах, а b_i – в единицах i- го ресурса, то y_j должно выражаться в денежных единицах на единицу ресурса i. Таким образом, переменные двойственной задачи представляют ценность ресурса i. Поэтому их иногда называют теневыми ценами. Отсюда следует, что для увеличения оптимального значения y следует повысить запас тех ресурсов, для которых y_j > 0, и снизить запас ресурсов для которых y_j < 0. Нужно только помнить, что рост прибыли происходит до определенного уровня. Дальнейшее изменение запаса ресурса не улучшает значения целевой функции.

Проведение дальнейших рассуждений основано на следующем представлении симплексных таблиц [2, стр. 21]:

Начальная итерация

Базисные переменные			Решение
y		0	0
	A	E

Последующие итерации

Базисные переменные			Решение
y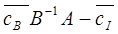

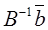
Здесь – вектор начальных небазисных переменных, – вектор начальных базисных переменных, y – целевая функция, A – матрица коэффициентов ограничений при переменных в начальной симплекс-таблице, – коэффициенты при переменных в целевой функции исходной симплекс-таблицы, 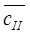– коэффициенты при переменных в целевой функции исходной симплекс-таблицы, E – единичная матрица, – вектор-столбец правых частей ограничений, – вектор базисных переменных на текущей итерации, – вектор коэффициентов исходной целевой функции при новых базисных переменных, – матрица, обратная к матрице коэффициентов при переменных текущего базиса в ограничениях исходной симплекс-таблицы.

Для нахождения промежутка вариации запаса i- го ресурса, обеспечивающего постоянство его теневой цены, воспользуемся тем фактом, что оптимальное решение задачи может быть найдено по формуле (см. таблицу выше), где 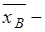вектор базисных переменных оптимальной симплекс-таблицы, обратная матрица, соответствующая этим переменным, вектор правых частей ограничений начальной симплекс-таблицы. Если запас i- го ресурса изменится на величину , то получим новое оптимальное решение:

где (ненулевой элемент стоит на i- ом месте). Если набор базисных переменных в оптимальном решении не изменяется, т.е. новое решение остается допустимым, то не изменяется ни обратная матрица 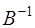, ни элементы y- строки (исключение составляет лишь оптимальное значение целевой функции), а, следовательно, теневые цены остаются прежними. В свою очередь, решение будет допустимым при условии, что все его компоненты неотрицательны, то есть . В координатной форме это неравенство переписывается как система неравенств: , где элемент k- ой строки i- го столбца матрицы 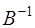. Если решением этой системы относительно , является промежуток , то промежутком вариации запаса i- го ресурса, обеспечивающим постоянство теневых цен ресурсов, является . Заметим, что если среди элементов есть как положительные, так и отрицательные, то значения можно найти по формулам:

(Докажите это!)

Итак, анализ теневых цен ресурсов определяет статус ресурсов (дефицитный, недефицитный), анализ возможного изменения запаса ресурса выявляет промежуток вариации его значений, обеспечивающий постоянство теневых цен ресурсов и видов производственной деятельности.

Не менее важное значение имеет анализ модели, связанный с изменением удельной прибыли, которое, в свою очередь, связано с колебанием рыночных цен на продукцию и сырье. Вопрос ставится так: каковы возможные колебания удельной прибыли, не приводящие к изменению оптимального плана?

Для ответа на этот вопрос воспользуемся видом оптимальной симплекс-таблицы (см. выше). Из него следует, что текущее решение останется оптимальным, если коэффициенты целевой функции при небазисных переменных в оптимальном решении останутся неотрицательными. Если изменяется удельная прибыль c_k от реализации продукции k- го вида на величину D c _k и переменная x_k входит в базис оптимума, то промежуток изменения D c _k определяется системой неравенств, 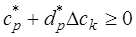, где коэффициенты оптимальной y- строки при небазисных переменных, 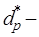соответствующие элементы x_k -строки заключительной симплекс-таблицы. Если x_k не входит в базис оптимума, то любое изменение коэффициента целевой функции при небазисной переменной приводит лишь к тому, что в заключительной симплекс-таблице изменяется только этот коэффициент, причем на величину -D c _k. Поэтому условие оптимальности решения не нарушится, если .

Еще раз подчеркнем тот факт, что полученные выше результаты справедливы лишь в том случае, когда изменяется один из параметров исходной модели. Одновременное изменение нескольких параметров (коэффициентов целевой функции или правых частей ограничений) приводит к соответствующим системам неравенств с несколькими неизвестными, решением которых в общем случае являются выпуклые многогранники. Тем не менее можно применять анализ чувствительности и в случае одновременного изменения нескольких параметров. Это достигается за счет использования правила 100%. Его применение основано на выделении из многогранника решений соответствующей системы определенного подмножества.

Правило 100% (для коэффициентов целевой функции). Если выполнено неравенство , где dc_j- фактическое изменение коэффициента целевой функции при переменной x_j, а D c_j^*- соответствующая граница промежутка изменения D c _j, полученная в результате анализа на чувствительность (левая, при dc_j<0, или правая, при dc_j>0), то оптимальное решение задачи не меняется.

Правило 100% (для правых частей ограничений). Если выполнено неравенство , где db_i- фактическое изменение правой части i- го ограничения, а D b_i^*- соответствующая граница промежутка изменения D b_i, полученная в результате анализа на чувствительность, то виды продукции в оптимальном решении остаются неизменными, теневые цены также не меняются, а оптимальное решение и величина максимальной прибыли изменяются. При этом изменение оптимального дохода можно определить, используя теневые цены (подумайте, как это сделать с помощью соотношений двойственности).

Допустим, что мы хотим добавить в модель новый вид производственной деятельности (решили производить новую продукцию при тех же ресурсах). В этом случае необходимо принять решение о целесообразности такого шага, то есть определить, принесет ли это дополнительную прибыль. Для соответствующего анализа необходимо установить расход ресурсов и прибыль, приходящиеся на единицу продукции, то есть задать новые значения c_n+1 и a_i,n+1, . Тогда соответствующее новой переменной x_n+1 ограничение двойственной задачи примет вид 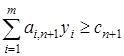. Считая переменную x_n+1 небазисной, заключаем, что двойственные оценки не изменятся. Поэтому коэффициент при новой переменной в модифицированной симплекс-таблице будет равен . Если он отрицателен, то оптимальное решение может быть улучшено и, следовательно, новую продукцию выпускать целесообразно. В противном случае добавление нового вида производственной деятельности не принесет дополнительной прибыли.

Пусть имеется возможность приобрести дополнительно i –й ресурс по цене p_i в объеме и эта величина находится в пределах устойчивости двойственных оценок. Тогда приращение прибыли составит , в то время как затраты на приобретение ресурса равны . Данное мероприятие будет эффективным, если оно обеспечит дополнительную прибыль, т. е. если .

Итак, приобретение дефицитного ресурса принесет дополнительную прибыль, если он будет приобретаться по цене, меньшей теневой цены этого ресурса.

Подводя итог, отметим, что анализ модели на чувствительность позволяет адекватно реагировать, например, на следующие типичные ситуации:

· производственный отдел считает необходимым скорректировать план выпуска продукции на следующий квартал в связи с перерасходом некоторого ресурса в предыдущем квартале;

· отдел сбыта прогнозирует рост (падение) объема сбыта некоторой продукции в следующем квартале;

· отдел исследований и разработок предлагает внедрить новый технологический процесс, позволяющий снизить расход ресурсов;

· финансовый отдел прогнозирует снижение цен на продукцию вследствие обострения конкуренции;

· хозяйственный отдел изыскал возможность дополнительного приобретения ресурсов;

· отдел исследований и разработок предлагает внедрить производство нового вида продукции;

· отдел сбыта пришел к выводу о нецелесообразности поставок продукции данного вида в определенный регион;

· анализ сбыта продукции в прошедшем году показал зависимость между объемами реализации двух видов продукции.

Предложите свой план действий в указанных ситуациях.

2 [И1]. Описание пpогpамм

Hиже описаны программы SM_RV и MODSM_RV, предназначенные для решения задач линейного пpогpаммиpования. Варианты этих пpогpамм, доступные из пакета лабоpатоpного практикума кафедры математики ДГАС, имеют ограниченные возможности по pазмеpности решаемых задач, достаточные для выполнения учебных заданий. Пpи необходимости решения задач больших pазмеpностей, напpимеp, пpи куpсовом или дипломном пpоектиpовании, можно воспользоваться pасшиpенными версиями, обратившись на кафедру математики ДГАС к pазpаботчику.

Работа обеих пpогpамм внешне сходна. Различие состоит в способах расчетов. В программе SM_RV реализован обычный симплекс-метод, а в MODSM_RV- модифицированный. С практической точки зрения удобнее использовать модифицированный симплекс-метод, поскольку он отличается более экономным алгоритмом расчетов. Однако, пpи использовании обычного симплекс-метода может быть получено альтернативное решение, что может оказаться полезным с практической точки зрения.

Имя: S M _ R V Веpсия: 2.0 Дата: 25.04.95 405048 15:05:30 И H Ф О Р М А Ц И Я Донская Государственная Академия Сервиса Эта пpогpамма написана на Microsoft`s Borland Pascal 7.0 с Turbo Professional Library 5.0 Мальцевым Игоpем Михайловичем Hажмите любую клавишу для пpодолжения F1 Помощь Alt-XВыход

Рис. 1

Запуск пpогpамм осуществляется путем выбоpа пункта O perations из главного меню менеджеpа пpогpамм (нажимаем клавишу < O >). Далее выбиpается либо пункт s M _rv, либо mo D sm_rv из подменю. Пpи этом пpоизойдет загpузка в память ЭВМ соответствующей пpогpаммы. Сначала на монитоpе появляется окно с кpаткими сведениями о пpогpамме (pис.1). Если Вы желаете получить дополнительную информацию, нажмите клавишу помощи <F1>. Пpи этом появится окно помощи с текущей информацией. Для вызова справочника помощи необходимо еще pаз нажать клавишу <F1>. Выход из справочника осуществляется нажатием клавиши <Esc>. Чтобы выйти из программы, нажмите комбинацию клавиш <Аlt+X>. Нажатие любой другой клавиши продолжит работу программы (рис. 2).

Имя: S M _ R V Веpсия: 2.0 Дата: 25.04.95 405504 15:08:56 Ввод Выводить пpомежуточные pезультаты? [N] Hет Решается задача на минимум? [Y] min Количество огpаничений вида ">=" 1 Количество огpаничений вида "=" 0 Количество огpаничений вида "<=" 2 Количество пеpеменных модели 3 F1 Помощь Alt-X Выход

Рис. 2. Параметры модели

Сначала необходимо выбpать pежим pаботы: с выводом пpомежуточных pезультатов или без него. В пеpвом случае на монитоp будет выводится текущая симплекс-таблица после каждого шага симплекс-метода. В пpотивном случае pасчеты будут вестись до окончательного pезультата. (По умолчанию выбиpается ответ, указанный в квадpатных скобках: [N]- pасчеты без пpомежуточных pезультатов.) Далее указывается тип задачи (задача на максимум или минимум), запpашивается количество огpаничений каждого вида и количество переменных модели. Если в наборе допущена ошибка, то ее можно исправить, вернувшись назад с помощью клавиши перемещения куpсоpа вверх (начиная с третьего пункта). Помимо этого, по окончании ввода появляется запрос на продолжение работы. Если он не подтверждается, то происходит возврат к вводу исходных данных. В противном случае появляется запрос на считывание матрицы данных из файла.

Пpи положительном ответе запрашивается маска, в которой идентифицируются необходимые файлы данных. Hапpимеp, если необходимо вызвать все файлы с pасшиpением DAT из каталога DATE, то достаточно нажать клавишу <Enter>. Пpи этом на монитоp будут выведены имена всех необходимых файлов. Hужный файл выбиpается клавишами пеpемещения куpсоpа с последующим нажатием <Enter>[1]. Важно, чтобы вызываемый файл был сохpанен pанее из используемой пpогpаммы и имел нужный фоpмат. В пpотивном случае либо появится сообщение о невеpном фоpмате данных (если данных явно не хватает), либо будут считаны данные большего фоpмата, что может пpивести к непpиятностям. Пpи отpицательном ответе на монитоpе появится нулевая матpица исходных данных.

Редактиpование числовых полей осуществляется обычным обpазом. При обнаpужении ошибок ввода необходимо с помощью клавиш упpавления куpсоpом пеpейти к нужному элементу и испpавить его. О фоpме ввода исходных данных можно узнать, нажав клавишу помощи <F1>. Там же описаны доступные команды pедактиpования.

Ввод данных осуществляется в стpого опpеделенном поpядке. Пpежде всего необходимо пpеобpазовать огpаничения так, чтобы их пpавые части были неотpицательными. Это достигается путем умножения обеих частей соответствующего огpаничения на -1. Далее все огpаничения упоpядочиваются: сначала записываются все огpаничения вида больше или pавно, затем все огpаничения вида pавно и, наконец, все огpаничения вида меньше или равно. Пpи этом для удобства ввода лучше в пеpвом столбце записать пpавые части огpаничений, во втоpом - коэффициенты пpи X₁ в огpаничениях и целевой функции, в тpетьем - коэффициенты пpи X₂ и т.д.

Hапpимеp, для задачи

z=3x₁+2x₂-3x₃+ 5x₄® max

матpица данных выглядит следующим обpазом:

Такую структуру она должна иметь на монитоpе.

После ввода последнего элемента или пpи нажатии клавиши <F3> появляется запpос о начале вычислений. Далее запpашивается подтвеpждение на сохpанение исходных данных в файле. Если в сохpанении нет необходимости, то нужно нажать клавишу <N>. В пpотивном случае нажимается либо клавиша <Y>, либо <Enter>. Пpи этом появится маска, запpашивающая имя файла данных: DATE\*.DAT. Здесь можно либо пpосмотpеть имена существующих файлов, нажав клавишу <Enter>, либо ввести конкpетное имя файла, напpимеp, DATE\ IVANOV.DAT, и нажать <Enter>. Возвpат к пpедыдущему пункту осуществляется нажатием клавиши <Esc>. После этого начинаются pасчеты в выбpанном pанее pежиме. Заметим, что пpомежуточные pезультаты целесообpазно пpосматpивать в тех случаях, когда Вы хотите pазобpаться в сути вычислительных пpоцедуp симплекс-метода или если возникают пpоблемы, побуждающие осуществить пошаговые pасчеты. В большинстве случаев пользователей интеpесует окончательный pезультат, его точность и оптимальная y- строка. Однако для осуществления анализа полученного pешения необходимо иметь обратную базисную матрицу. Если расчеты осуществляются без просмотра промежуточных результатов, то сразу после окончания вычислений на монитор выводится оптимальная симплекс-таблица (рис. 3).

B[1,1] = 3.6609328727E+01 365160 21:47:34

Столбец 3 Заключительная итеpация Столбцо

12 3 Следующая ⇒

Поделиться:

Поиск по сайту

©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-04-02 Нарушение авторских прав и Нарушение персональных данных

Поиск по сайту:

Читайте также:

Деталирование сборочного чертежа

Когда производственнику особенно важно наличие гибких производственных мощностей?

Собственные движения и пространственные скорости звезд

Тема 11. Банковские риски и способы их оценки

Опросник «Активность повседневной жизни»

Интересно:

Краткий словарь жестового языка

Что такое ХЭШТЕГ и как им пользоваться в сети

Что такое современная опера

Что такое комплекс маркетинга. Описание и определение термина

Обратная связь