Модуляцией
При частотной модуляции по закону модулирующего колебания U(t) изменяется частота высокочастотного несущего колебания.
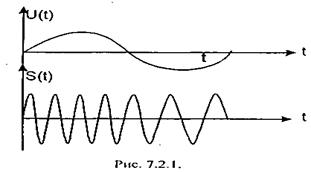На рис.2.1 показаны графики модулирующего и модулированного сигналов в случае модуляции чистым тоном. Получим аналитическое выражение для ЧМ- колебания. При модуляции чистым тоном
, (2.1)
где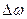 
- максимальное отклонение, называемое девиацией частоты, а 
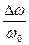- относительное изменение частоты. Пo своему определению мгновенная круговая частота является производной по времени от аргумента тригонометрической функции cosψ(t), представляющей колебание, т.е.
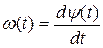. (2.2)
Из последнего выражения получим
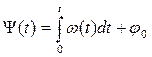, (2.3)
т.е. фаза колебания определяется интегралом от круговой частоты. Поэтому для ЧМ - колебания при модуляции чистым томом можно записать
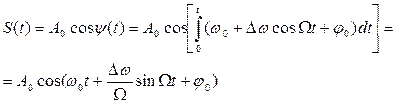(2.4)
Замечаем, что изменение частоты по закону 
приводит к изменению фазы по закону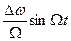 
. Величина 
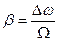называется индексом частотной модуляции и имеет смысл максимальной величины (амплитуды) изменения фазы при частотной модуляции.
Заменяя косинус суммы двух углов по известным формулам тригонометрии, вместо (2.4) при 
= 0 получим
(2.5)
Определим теперь спектр частотно-модулированного сигнала. Начнем со случая малого индекса модуляции, когда β <<1.В этом случае
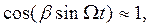
(2.6)
S(t)=A0cosωt + 0,5βA0cos(ω0 + Ω)t – 0,5βA0cos(ω0 – Ω)t (2.7)
Замечаем, что при малом индексе модуляции спектр ЧМ колебания отличается от спектра AM-колебания только сдвигом фазы нижней боковой частоты на 180".
Определим теперь спектр ЧМ - колебания при произвольном индексе модуляции. Для этого периодические функци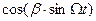и 
и 
разложим в ряды Фурье, коэффициенты которых, как доказывается в теории бесселевых функций, являются функциями Бесселя первого рода:
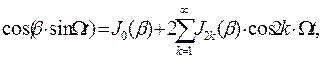(2.8)
sin(βsinΩt) = 2∑ J(2k-1)(β)sin(2k-1)Ωt. (2.9)
Аналогично можно записать и такие равенства
sin(βcosΩt) = 2∑(-1)k+1 J(2k-1)(β)sin(2k-1)Ωt,
cos(βcosΩt) = J0(β)+ 2∑(-1)k J2k(β)sin2kΩt,
где k =1,2,3.........
Подставляя выражения (2.8) и (2.9) в (2.5) и производя тригонометрические
преобразования, окончательно получим
(2.10)
Таким образом, ЧМ колебание при модуляции чистым тоном имеет дискретный спектр и состоит из несущей и бесконечного числа боковых частот ω0 + kΩ и ω0 – kΩ с амплитудами A0Jk(β). Однако практическая ширина спектра при ЧМ ограничена. Это можно заметить на рис.2.2, на котором приведены графики функций Jk(β). При β >>1 и k > β функции Jk(β) убывают так быстро, что ими можно пренебречь, т.е. считать, что Jk(β)=0. Поэтому ширина спектра при широкополосной ЧМ (β >> 1) будет равна
2Δω ≈ 2(β +1)Ω = 2Δ ω + 2Ω ≈ 2Δω, (2.11)
т.е. приближенно равна удвоенной девиации частоты. Таким образом, ширина спектра при широкополосной ЧМ в β +1 раз шире, чем при обычной АМ.
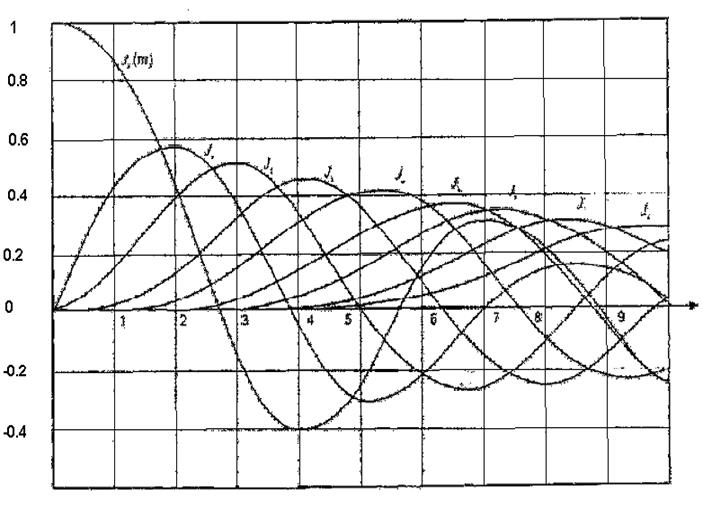
Рисунок 2.2 Графики функций Бесселя
Задание.
По заданному выражению частотно-модулированного сигнала, его параметрам и несущему колебанию записать спектральное представление ЧМ-сигнала и рассчитать следующие параметры:
- девиацию частоты, максимальное и минимальное значения частоты, ширину спектра;
- амплитуды и частоты спектральных составляющих;
- мощность спектральных составляющих ЧМ сигнала;
- построить амплитудную спектральную диаграмму ЧМ- сигнала;
Объяснить результаты графических построений и выполненных расчетов.
Все результаты представить в графической форме.