Уравнения амплитудно-модулированных колебаний

ДЕРЖАВНИЙ УНІВЕРСИТЕТ ТЕЛЕКОМУНІКАЦІЙ

МЕТОДИЧНІ ВКАЗІВКИ

До виконання контрольної роботи з дисципліни

 

«Теорія електрозв’язку»

 

 

Расчет характеристик и параметров сигналов с амплитудной

Модуляцией

 

Модуляция заключается в изменении одного или нескольких пара­метров переносчика в соответствии с передаваемым сообщением. При использовании в качестве переносчика высокочастотного гармониче­ского колебания модулированный сигнал в общем случае можно пред­ставить в виде:

.

В зависимости от того, какой из параметров А, ω или φ модулиру­ется, различают три вида модуляции: амплитудную (AM), частотную (ЧМ) и фазовую (ФМ). Всякое модулированное колебание несинусои­дально и имеет сложный спектр.

При амплитудной модуляции по закону управляющего сигнала U(t) изменяется амплитуда колебаний:

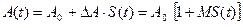, (1.1)

где ΔА – максимальное абсолютное изменение амплитуды, а - относительное изменение амплитуды, называемое коэффициентом модуляции.

АМ колебание записывается в виде:

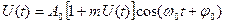, (1.2)

и для случая модуляции чистым тоном U(t)=cosΩt имеет вид, показанный на рис.1.1. Очевидно, чтобы не было искажений, коэффици­ент модуляции должен быть меньше единицы. Из графика AM колеба­ний видно, что:

,

,

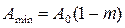откуда имеем:

(1.3)

 

 

 

 

Рис. 1.1.

 

 

Определим спектр AM колебаний при модуляции чистым тоном. Это можно сделать с помощью преобразования Фурье. Однако проще его получить с помощью простых тригонометрических преобразова­ний. Действительно, полагая в (1.2) U(t)=cosΩt, получим:

(1.4)

 

Замечаем, что AM колебание имеет дискретный спектр и со­стоит из трех некратных гармонических составляющих: колеба­ния несущей частоты с амплитудой А₀ и двух колебаний с амплитудами и частотами , которые называются боковыми частотами.

Спектр AM колебания показан на рис. 1.2. Ширина спектра АМ-сигнала равна 2Ω.

 

 

 

 

Рис. 1.2

 

В общем случае, когда модуляция осуществляется сложным периодическим сигналом, последний можно разложить в ряд Фурье:

(1.5)

а выражение для АМ-колебания представить в виде:

(1.6.)

 

В этом случае AM колебание состоит из колебания несущей часто­ты и двух боковых полос с суммарными и разностными частотами. Спектр такого колебания показан на рис. 1.3. Если спектр модулирующего колебания ограничен сверху частотой , то ширина спектра модулированного колебания равна .

Рис. 1.3.

 

Заметим, что огибающая амплитуд боковых частот с точностью до постоянного множителя совпадает с огибающей спектра ампли­туд модулирующей функции. Это позволяет легко построить ампли­тудный спектр AM колебания, если известен спектр модулирующей функции. Для построения необходимо сместить спектр модулирующей функции по оси частот на величину , получая при этом верхнюю бо­ковую полосу; нижняя боковая полоса будет являться зеркальным ото­бражением верхней относительно частоты .

При амплитудной модуляции гармонической несущей произволь­ным непериодическим сигналом с полосой частот от до спектр будет содержать составляющую несущей частоты и две боковые поло­сы.

Рассмотрим энергетические соотношения при AM. В соответствии с изменением амплитуды колебания изменяется и средняя за период высокой частоты мощность модулированного колебания.

Мощность сигнала в отсутствии модуляции (мощность несущего колебания) определяется первым членом выражения (3.4) и равна

(1.7)

где 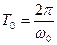- период высокочастотного колебания.

В режиме модуляции мощность непрерывно изменяется. Ее максимальное и минимальное значения определяются выражениями:

 

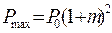, (1.8.)

Мощность двух боковых частот (при модуляции чистым тоном) и будет равна

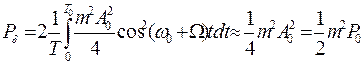1 (.9.)

Средняя за период модуляции мощность будет равна

 

1 (.10)

 

где - период модулирующего колебания.

 

 

Из последних выражений при m = 1 получим

 

, , , ,

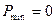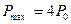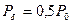Задание.

По заданному выражению модулирующего сигнала, его параметрам и несущему колебанию записать спектральное представление АМ-сигнала и рассчитать следующие параметры:

- амплитуды, фазы и частоты спектральных составляющих, ширину спектра;

- мощность спектральных составляющих АМ- сигнала;

- построить амплитудную и фазовую спектральные диаграммы;

- построить осциллограмму АМ сигнала.

Объяснить результаты графических построений и выполненных расчетов.

Все результаты представить в графической форме.

 

Уравнения амплитудно-модулированных колебаний

1 u(t)= 10[1 + 0,3cos(10⁴ t + π/6) + 0,5cos(5x10⁴ + π/4)] cos(10⁶ t + π/3)

2 u(t)= 8[1 + 0,4cos(2x10⁴ t + π/3) + 0,6cos(3x10⁴ + π/6)] sin(10⁶ t + π/4)

3 u(t)= 6[1 + 0,6sin(3x10⁴ t + π/12) + 0,2cos(5x10⁴ + π/4)] cos(10⁶ t + π/3)

4 u(t)=9 [1 + 0,8sin(4x10⁴ t + π/4) + 0,6cos(6x10⁴ + π/3)] sin(10⁶ t + π/6)

5 u(t)=4[1 + 0,5cos(2x10⁵ t + π/6) + 0,5cos(4x10⁵ + π/8)] cos(10⁷ t + π/8)

6 u(t)=8[1 + 0,6sin(10⁵ t + π/6) + 0,6cos(2x10⁵ + π/3)] cos(10⁷ t + π/4)

7 u(t)=12[1 + 0,7cos(3x10⁵ t + π/3) + 0,6cos(2x10⁵ + π/6)] sin(10⁷ t + π/6)

8 u(t)=10[1 + 0,8sin(2x10⁵ t + π/4) + 0,4cos(4x10⁵ + π/3)] sin(10⁷ t + π/3)

9 u(t)=8[1 + 0,6sin(4x10⁵ t + π/3) + 0,8cos(6x10⁵ + π/6)] sin(3x10⁷ t + π/4)

10 u(t)=7[1 + 0,7cos(3x10⁵ t + π/6) + 0,9cos(5x10⁵ + π/4)] cos(10⁷ t + π/3)

11 u(t)=6[1 + 0,6sin(2x10⁵ t + π/8) + 0,7cos(4x10⁵ + π/3)] cos(10⁷ t + π/4)

12 u(t)=9[1+ 0,5cos(3x10⁵ t + π/4) + 0,6cos(5x10⁵ + π/6)]sin(2x10⁷ t + π/3)

13 u(t)=10[1+ 0,6cos(4x10⁴ t + π/6) + 0,5cos(3x10⁴ + π/8)] cos(10⁶ t + π/6)

14 u(t)=8[1+ 0,8cos(10⁴ t + π/3) + 0,6cos(2x10⁴ + π/3)] sin(2x10⁶ t + π/8)

15 u(t)=6[1+ 0,9sin(2x10⁴ t + π/8) + 0,7cos(4x10⁴ + π/6)] cos(3x10⁶ t + π/3)

16 u(t)=5[1+ 0,8sin(10⁴ t + π/6) + 0,8cos(5x10⁴ + π/4)] sin(4x10⁶ t + π/6)

17 u(t)=7[1 + 0,7sin(10⁵ t + π/3) + 0,5cos(4x10⁵ + π/8)] sin(10⁷ t + π/4)

18 u(t)=6[1+ 0,8cos(2x10⁵ t + π/4) + 0,6cos(3x10⁵ + π/6)]cos(2x10⁷ t + π/3)

19 u(t)=10[1 + 0,6cos(3x10⁵ t + π/6) + 0,5cos(5x10⁵ + π/3)] sin(10⁷ t + π/4)

20 u(t)=8[1+ 0,9sin(2x10⁴ t + π/8) + 0,9cos(3x10⁴ + π/4)] cos(3x10⁶ t +π/3)

21 u(t)=7[1 + 0,6cos(10⁴ t + π/6) + 0,8cos(2x10⁴ + π/3)] cos(2x10⁶ t + π/8)

22 u(t)=9[1 + 0,5sin(3x10⁴ t + π/3) + 0,5cos(2x10⁴ + π/6)] cos(10⁶ t + π/3)

23 u(t)=5[1 + 0,8cos(10⁵ t + π/6) + 0,6cos(2x10⁵ + π/4)] sin(10⁷ t + π/3)

24 u(t)=10[1+ 0,7sin(2x10⁵ t + π/4)+ 0,7cos(3x10⁵ + π/3)]sin(2x10⁷ t + π/8)

25 u(t)=8[1 + 0,9cos(3x10⁴ t + π/8) + 0,8cos(2x10⁴ + π/4)] sin(10⁶ t + π/3)

26 u(t)=7[1 + 0,8sin(5x10⁴ t + π/6)+ 0,8cos(7x10⁴ + π/3)]cos(8x10⁶ t + π/4)

27 u(t)=6[1+ 0,9cos(8x10⁴ t + π/3) + 0,7cos(7x10⁴ + π/4)]cos(9x10⁶ t + π/8)