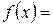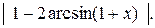Занятие 10
Построение графиков функций
1.Линейные преобразованияграфиков функций.
Во многих случаях графики элементарных функций можно построить по графику заданной его части или по графику другой функции с помощью линейных преобразований: параллельного переноса, растяжения (сжатия), преобразования симметрии.
О. 1.1. Пусть f – некоторая числовая функция с областью определения D(f). Тогда множество Гf точек 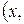
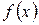 ) координатной плоскости, где
) координатной плоскости, где 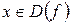 , называется графиком функции f.
, называется графиком функции f.
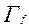 :=
:= 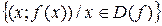 .
.
Рассмотрим вопрос построения графика новой функции 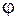 , при помощи различных преобразований графика функции f и ее аргумента. Пусть построен график функции
, при помощи различных преобразований графика функции f и ее аргумента. Пусть построен график функции 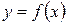 . Прежде чем приступить к построению
. Прежде чем приступить к построению 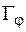 , следует сначала расчленить функцию φ на более простые функции, записав цепочку преобразований.
, следует сначала расчленить функцию φ на более простые функции, записав цепочку преобразований.
Выясним, какие преобразования следует осуществить над Гf, чтобы получить график искомой функции φ, задаваемой следующими выражениями:
1)  (х)=f(х - а); 2)
(х)=f(х - а); 2)  (х)=f(х) + А;
(х)=f(х) + А;
3)  (х)=kf(x); 4)
(х)=kf(x); 4)  (х)=f(kx);
(х)=f(kx);
5)  (х)=f(- x); 6)
(х)=f(- x); 6)  (х)= - f(x);
(х)= - f(x);
7) 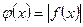 ; 8)
; 8) 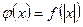 .
.
Удобно оформить преобразования графика функции в виде следующей таблицы:
Таблица 1.
| № | Общий вид функции | Преобразования, которые следует осуществить над 
| Иллюстрация |
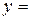 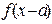
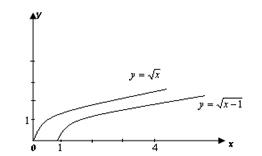
| Параллельный перенос графика функции 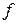 вдоль оси абсцисс на | a | единиц
· вправо, если a > 0;
· влево, если, a < 0. вдоль оси абсцисс на | a | единиц
· вправо, если a > 0;
· влево, если, a < 0.
|  
| |
| y = f (x) + А | Параллельный перенос графика функции 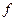 вдоль оси ординат на
| А | единиц вдоль оси ординат на
| А | единиц
| 
| |
| y = kf (x) |
| 
| |
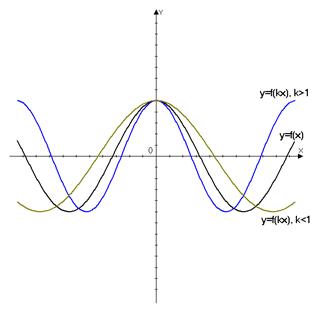
| y = f (kx) |
· При 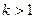 сжатие сжатие  к точке к точке 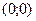 вдоль оси вдоль оси  в в 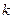 раз.
· При раз.
· При 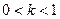 , растяжение от точки , растяжение от точки 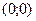 вдоль оси вдоль оси  в в 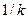 раз. раз.
| 
| |
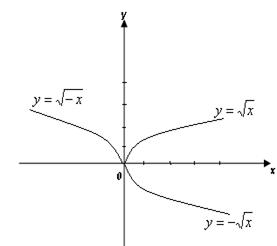
| a) y = f (− x); b) y = − f (x) | а) Симметричное отражение Гf относительно оси 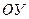 .
b) Симметричное отражение Гf относительно оси .
b) Симметричное отражение Гf относительно оси  
| 
| |
| y = | f (x) | |
При f (x) 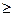 0 график функции 0 график функции 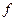 остаётся без изменений,
при f (x) < 0 — график симметрично отражается относительно оси остаётся без изменений,
при f (x) < 0 — график симметрично отражается относительно оси  . .
| 
| |
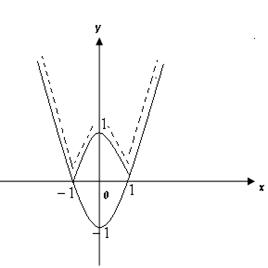
| y = f (| x |) |
При 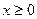 — график остаётся без изменений,
при x < 0 — график симметрично отражается относительно оси — график остаётся без изменений,
при x < 0 — график симметрично отражается относительно оси 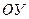 . .
| 
|
Пример 1. Построить графики функций а) 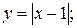 б)
б) 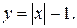
Δ а) Согласно случаю 6. таблицы 1 для построения графика функции 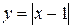 нужно воспользоваться графиком линейной функции
нужно воспользоваться графиком линейной функции 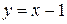 , оставив без изменения часть графика этой функции, которая лежит выше оси
, оставив без изменения часть графика этой функции, которая лежит выше оси  , а часть графика, которая находится ниже оси
, а часть графика, которая находится ниже оси  , симметрично отражается относительно оси
, симметрично отражается относительно оси  (см. рис. 1).
(см. рис. 1).
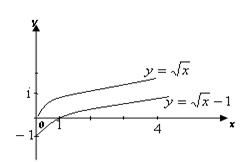
б) Согласно случаю 7. таблицы 1 для построения графика функциинужно оставить без изменения часть графика линейной функции 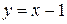 для
для 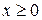 , а другую часть графика (для x < 0) удалить, а затем симметрично отобразить относительно оси
, а другую часть графика (для x < 0) удалить, а затем симметрично отобразить относительно оси 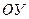 оставшуюся часть графика (см. рис. 2).
оставшуюся часть графика (см. рис. 2).
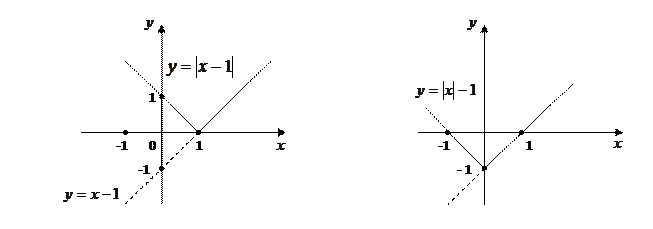
Рисунок 1 Рисунок 2
 Пример 2. Построить график функции
Пример 2. Построить график функции 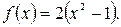
Δ Запишем следующую цепочку преобразований:
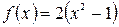

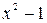

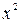
Гf Г2 Г1
Рисунок 3
Из цепочки преобразований видим, что: Г2 получается сдвигом Г1 вниз на 1 единицу. Гf получается при помощи растяжения Г2 по оси 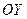 в 2 раза.
в 2 раза.
Строим теперь эскиз Гf (см. рис. 3).
 Пример 3. Построить график функции
Пример 3. Построить график функции 
Δ По свойству модуля 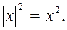
Поэтому 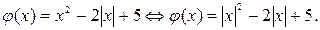
Составим следующую цепочку преобразований:
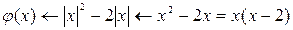
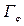

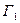
Заметим, что график функции Г1- есть парабола, которая пересекает ось 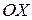 , в точках
, в точках 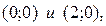 вершина параболы находится в точке
вершина параболы находится в точке  .
. 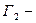 объединение правой части
объединение правой части  с ее зеркальным отражением в оси
с ее зеркальным отражением в оси  (см. рис. 4);
(см. рис. 4);  получается из графика
получается из графика  сдвигом вверх на 5 единиц (см. рис. 5).
сдвигом вверх на 5 единиц (см. рис. 5).
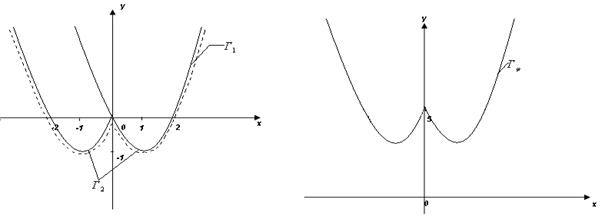
Рисунок 4 Рисунок 5
2.Некоторые примеры и схемы построения эскизов графиков функций
2.1. Пусть требуется построить эскиз 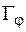 графика функции
графика функции 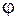 , заданной равенством
, заданной равенством 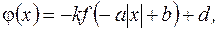 где
где 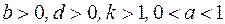 .
.
Сначала нужно расчленить функцию 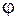 на более простые функции, записав цепочку преобразований. Порядок построения
на более простые функции, записав цепочку преобразований. Порядок построения 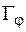 , начиная от первичного графика
, начиная от первичного графика 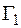 , указывается стрелками.
, указывается стрелками.
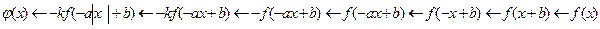
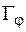
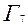
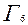
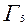
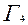
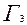
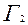
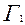
Пользуясь таблицей и выписанной цепочкой, следует объяснить, каким преобразованием получается 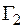 из
из 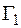 ,
, 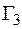 из
из 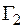 и т.д.,
и т.д., 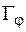 из
из 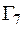 . После чего приступить к последовательному построению графиков. Для рассматриваемого случая имеем следующие объяснения:
. После чего приступить к последовательному построению графиков. Для рассматриваемого случая имеем следующие объяснения:
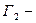 сдвиг
сдвиг 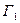 влево вдоль оси
влево вдоль оси  на
на 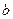 единиц.
единиц.
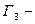 зеркальное отражение
зеркальное отражение  в оси
в оси 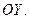
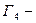 растяжение
растяжение 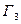 от оси
от оси 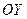 вдоль оси
вдоль оси  в
в 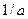 раз.
раз.
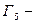 зеркальное отражение
зеркальное отражение  в оси
в оси  .
.
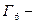 растяжение
растяжение 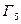 от оси
от оси  вдоль оси
вдоль оси 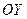 в
в 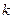 раз.
раз.
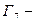 объединение правой части
объединение правой части 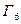 с его зеркальным отражением в оси
с его зеркальным отражением в оси 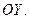 .
.
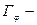 сдвиг
сдвиг 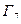 вдоль оси
вдоль оси 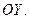 вверх на
вверх на 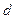 единиц.
единиц.
Заметим, что расчленение функции  в цепочку более простых, вообще говоря, неоднозначно. Однако следует помнить, что величина сдвига вдоль оси
в цепочку более простых, вообще говоря, неоднозначно. Однако следует помнить, что величина сдвига вдоль оси  определяется той постоянной, которая прибавляется к
определяется той постоянной, которая прибавляется к 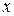 , a не к
, a не к  «
« », и тем более не к «
», и тем более не к «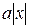 ». Поэтому для отыскания этой постоянной следует сначала освободить
». Поэтому для отыскания этой постоянной следует сначала освободить 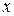 от знака модуля и коэффициента а.
от знака модуля и коэффициента а.
Пример 4. Построить график функции Гf, где f(х)= 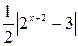
Δ Запишем следующую цепочку преобразований:
f(х) 
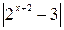

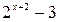



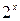
Гf Г4 Г3 Г2 Г1
Из которой ясно, что:
Г2 – получается сдвигом Г1 влево на 2 единицы.
Г3 - получается сдвигом Г2 вниз на 3 единицы.
Г4 – часть графика Г3, находящаяся ниже оси  , отразится зеркально в оси
, отразится зеркально в оси 
Гf – сжатие Г4 к оси  с коэффициентом равным 2.
с коэффициентом равным 2.
Строим теперь эскиз Гf (см. рис. 6):

Рисунок 6
Пример 5. Построить график функции 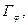 где
где 
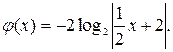
Δ Запишем следующую цепочку преобразований:
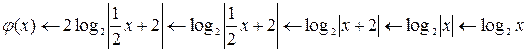
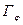
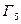

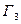

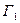
При этом:
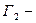 объединение правой части
объединение правой части 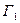 с его зеркальным отражением в оси
с его зеркальным отражением в оси 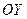 .
.
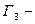 результат сдвига
результат сдвига  влево на 2 единицы.
влево на 2 единицы.
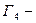 результат растяжения
результат растяжения 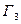 от оси
от оси 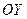 с коэффициентом растяжения 2.
с коэффициентом растяжения 2.
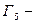 результат растяжения
результат растяжения  от оси
от оси  с коэффициентом растяжения 2.
с коэффициентом растяжения 2.
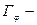 зеркальное отображение графика
зеркальное отображение графика 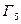 в оси
в оси  .
.
Строим теперь эскиз графика функции 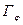 (см. рис. 7).
(см. рис. 7).
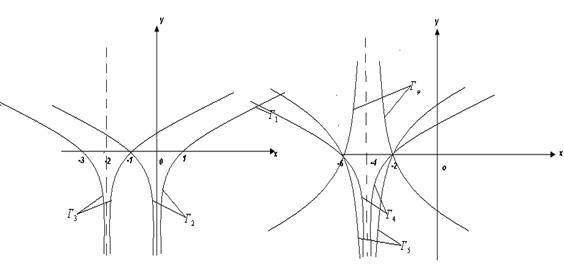
Рисунок 7
2.2. Построение графика дробно-линейной функции 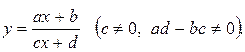
Выделив целую часть, представим функцию в виде:  (1) Тогда нетрудно заметить, что искомый график представляет собой график функции
(1) Тогда нетрудно заметить, что искомый график представляет собой график функции 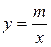 (гиперболу), смещённый на
(гиперболу), смещённый на 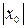 вправо по оси Ох, если
вправо по оси Ох, если 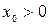 , влево - если
, влево - если 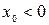 ; и на
; и на 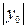 вверх по оси Оу, если
вверх по оси Оу, если 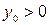 , вниз – если
, вниз – если 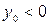 (см. рис. 8).
(см. рис. 8).
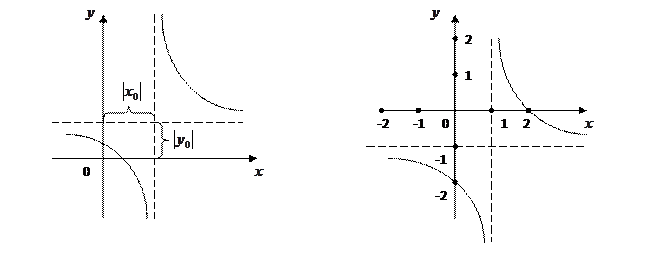
Рисунок 8 Рисунок 9
Например, график дробно-линейной функции 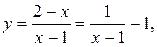
построенный изложенным выше способом, изображён на рисунке 9.
Учебная карта к занятию 10.
Задания уровня А
1.1 Построить графики функций: а)  б)
б) 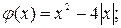
в) 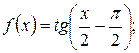 г)
г) 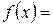
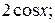 д)
д) 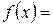

Задания уровня В
2.1 Построить графики функций: а) 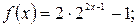 б)
б) 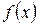
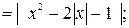
в) 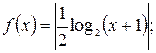 г)
г) 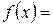
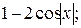 д)
д) 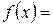
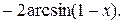
Задания уровня С
3.1 Построить эскиз графика функции 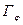 , где а)
, где а) 
б) 
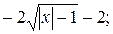 в)
в) 
Домашнее задание
1.2 Построить графики функций: а)  б)
б) 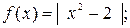
в) 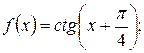 г)
г) 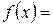
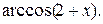
2.2 Построить графики функций: а) 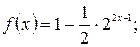 б)
б) 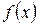
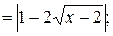
в) 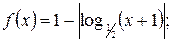 г)
г) 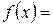
 д)
д)