Основные свойства проекторов и инъекторов

БИЕКТОРЫВ КОНЕЧНЫХ ГРУППАХ

 

Исполнитель:

студент группы H.01.01.01 М-43

Векшин П.А.

 

Научный руководитель:

доктор физико-математических наук,

профессор Скиба С.В.

 

Гомель 2003

Содержание

 

Введение

1. Основные обозначения

2. Используемые результаты

3. Основные свойства проекторов и инъекторов

4. Биекторы и их свойства

Заключение

Список использованных источников

Введение

 

В настоящей курсовой работе излагается материал на тему: "Биекторы конечных групп". Цель моей работы состоит в том, чтобы исследовать свойства конечной разрешимой группы с заданными инвариантами подгруппы Шмидта.

Моя курсовая работа состоит из четырех пунктов. В первом пункте изложены основные обозначения, которые используются в данной работе.

Во втором пункте были введены используемые результаты для дальнейшего изучения биекторов и их свойств. Здесь излагаются шесть теорем, три следствия и шесть лемм.

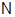В третьем пункте изложены основные свойства проекторов и инъекторов, даны определения подгруппы группы, максимальной подгруппы группы, инъектора и биектора. Так же рассмотрены два примера -биекторов, -биекторов, а так же пример, когда группа не является метанильпотентной, но 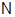-проекторы и 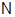-инъекторы совпадают между собой.

В четвертом пункте изучена и рассмотрена сама тема моей курсовой работы, которая и является названием данного пункта. Здесь показывается, что -биекторы во всех разрешимых группах существуют только в случае, когда 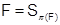совпадает с классом всех разрешимых -групп. Кроме того, устанавливается, что в метанильпотентных группах существование -биекторов, превращает его в -холловскую подгруппу.

Также в этом пункте изучены и доказаны следующие основные теоремы, (1),(2).

При доказательстве некоторых теорем и лемм использовались ссылки на теоремы, следствия и леммы, формулировки которых можно найти в используемых результатах.

Завершает мою курсовую работу список используемой литературы, который состоит из пяти источников.

Основные обозначения

 

	группа
	класс всех разрешимых групп
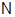
	класс всех нильпотентных групп
	является подгруппой группы
	является нормальной подгруппой группы
	прямое произведение подгрупп и
	подгруппа Фраттини группы
	фактор-группа группы по
	множество всех простых делителей натурального числа
	множество всех простых делителей порядка группы
	коммутант группы
	индекс подгруппы в группе

 

Используемые результаты

 

Лемма Если --- класс Шунка, то .

Лемма Пусть --- класс Шунка и --- конечная нильпотентная группа. Если --- подгруппа из , то является -проектором в тогда и только тогда, когда --- -холловская подгруппа.

Лемма Пусть --- радикальный класс и --- конечная нильпотентная группа. Если --- подгруппа из , то является -инъектором в тогда и только тогда, когда --- -холловская подгруппа.

Теорема Если --- класс Фиттинга и --- гомоморф, то .

Следствие Если и --- радикальные формации, то .

Теорема Если --- разрешимый класс Шунка, а --- разрешимая насыщенная формация, то --- разрешимый класс Шунка.

Следствие Если и --- разрешимые насыщенные формации, то --- разрешимая насыщенная формация.

Теорема Если и --- классы Фиттинга, то --- класс Фиттинга и .

Лемма Пусть --- разрешимая группа, тогда

1) если , то ;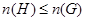

2) если 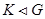, то ;

3) если , то .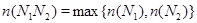

В частности, если и --- разрешимые группы ;

4) .

Теорема Для любого класса Шунка в каждой разрешимой группе любой -проектор является -покрывающей подгруппой и любые две -покрывающие подгруппы группы сопряжены между собой.

Лемма Пусть --- разрешимая группа. Тогда:

1) ;

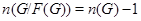2) .

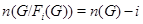Лемма Для любого гомоморфа и любой группы справедливы следующие утверждения:

1) если - -проектор группы и максимальна в , то - -покрывающая подгруппа группы ;

2) если - -покрывающая подгруппа в группе и , то - -покрывающая подгруппа в ;

3) если - -покрывающая подгруппа группы и , то - -покрывающая подгруппа фактор-группы ;

4) если и --- -покрывающая подгруппа фактор-группы , то каждая -покрывающая подгруппа из является -покрывающей подгруппой из .

Теорема Пусть --- класс Фиттинга и --- разрешимая группа. Тогда является -инъектором группы тогда и только тогда, когда будет -максимальной в и --- -инъектор коммутанта .

Следствие Пусть --- класс Фиттинга и --- разрешимая группа. Если --- -инъектор группы и , то --- -инъектор в .

Теорема Если --- максимальная подгруппа разрешимой группы , то ,где .

Основные свойства проекторов и инъекторов

Определение. Пусть --- группа и --- класс групп. Если и , то --- -подгруппа группы .

Определение. -максимальной подгруппой группы называется такая -подгруппа группы , которая не содержится ни в какой большей -подгруппе.

Определение. -проектором группы называется такая подгруппа группы , что 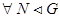, является максимальной в .

Определение. Пусть --- класс групп. Подгруппа группы называется -инъектором, если для каждой субнормальной подгруппы группы пересечение является -максимальной подгруппой в .

Определение. Пусть --- класс групп. Подгруппа группы называется -биектором, если является -максимальной подгруппой в , а является -максимальной в для каждой нормальной подгруппы .

Ясно, что -биектор одновременно является -проектором и -инъектором группы .

Пример Примерами -биекторов служат силовские -подгруппы групп для класса 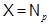всех -групп.

Пример В группе силовская 2-подгруппа является -биектором.

Пример Группа не является метанильпотентной, но -проекторы и -инъекторы совпадают между собой и являются нехолловыми подгруппами порядка 24.

 

Биекторы и их свойства

 

Для локальной формации каждая конечная разрешимая группа обладает единственным классом мопряженных -проекторов. Если --- радикальный класс, т. e. класс Фиттинга, то каждая конечная разрешимая группа содержит единственный класс сопряженных -инъекторов. Но наиболее употребительными в современной алгебре классы конечных групп являются одновременно и локальными формациями, и радикальными классами. Поэтому вполне естественно встает вопрос о существовании -биекторов в конечных разрешимых группах для локальной радикальной формации .

В настоящей работе показывается, что -биекторы во всех разрешимых группах существуют только в том случае, когда совпадает с классам всех разрешимых -групп. Кроме того устанавливается, что в метанильпотентных группах существование -биектора превращает его в -холловскую подгруппу, и приведен пример, показывающий, что в разрешимых группах ступени нильпотентности это свойство нарушается.

Пусть --- класс групп. Через обозначается совокупность всех простых чисел , для которых в существует неединичная -подгруппа, т. е. . Множество называется характеристикой класса .

Для любого множества простых чисел 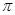через обозначается класс всех нильпотентных 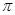-групп.

 

Лемма Если --- класс Шунка, то .

 

Доказательство. Пусть 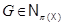. Ясно, что примитивная нилпотентная группа имеет простой порядок. Если --- произвольная примитивная факторгруппа группы , то имеет простой порядок . Так как , то . Из определения класса Шунка получаем, что . Таким образом, . Обратно, если , то для любого простого делителя порядка существует подгруппа индекса . Так как , то и 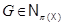. Лемма доказана.

 

Следствие Если --- локальная формация, то .

 

Доказательство. Достаточно вспомнить, что локальная формация является насыщенной, а значит и классом Шунка.

 

Лемма Пусть --- класс Шунка и --- конечная нильпотентная группа. Если --- подгруппа из , то является -проектором в тогда и только тогда, когда --- -холловская подгруппа.

Доказательство. Пусть --- -проtктор в группе . Так как , то по лемме подгруппа является -подгруппой. Пусть --- -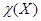холловская в подгруппа. Ясно, что . Nак как 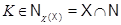, то --- -подгруппа и .

Обратно, пусть --- -холловская подгруппа и пусть --- -проектор в . Так как , то --- -подгруппа и .

 

Лемма Если --- радикальныи класс, то .

 

Доказательство. Если , то в существует субнормальная подгруппа простого порядка , для любого 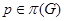. Поэтому , , и .

Обратно, пусть 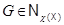, тогда для каждого 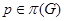в существует подгруппа . Значит все -подгруппы содержатся в . Так как замкнут относительно прямых произведений, то . Лемма доказана.

 

Лемма Пусть --- радикальный класс и --- конечная нильпотентная группа. Если --- подгруппа из , то является -инъектором в тогда и только тогда, когда --- -холловская подгруппа.

 

Доказательство. Пусть --- -инъектор в . Так как , то будет -подгруппой в . Если --- -холловская в подгруппа, то и --- -подгруппа. Поэтому .

Обратно, если --- -холловская подгруппа в , то . Если --- -инъектор, то и --- подгруппа, поэтому . Лемма доказана.

Пусть , где --- пробегает все группы из . Если --- разрешимый радикальный класс, то .

 

Следствие Пусть --- радикальный класс Шунка. Тогда в каждой конечной нильпотентной группе существует -биектор и подгруппа является -холловской подгруппой группы .

 

Доказательство получаем из лемм и.

Следствие Пусть --- радикальная локальная формация. Тогда в каждой нильпотентной группе существует -биектор и подгруппа 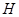является -холловской подгруппой группы .

 

Обозначим через совокупность всех -проекторов группы , а через совокупность всех -инъекторов.

 

Теорема Пусть --- радикальный класс Шунка. Если в конечной метанильпотентной группе существует -биектор 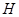, то 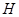является -холловской подгруппой группы .

 

Доказательство. Пусть . Так как в разрешимой группе все -проекторы и все -инъекторы сопряжены между собой, то .

Пусть --- подгруппа Фиттинга. Так как --- -инъектор в , то по лемме подгруппа является 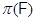-холловской подгруппой в .

Так как нильпотентна и является -проектором в , то будет 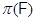-холловской подгруппой в по лемме. Поскольку , то 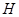- -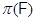подгруппа. Кроме того, и есть -число. Значит, --- -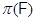холловская подгруппа.

Следствие Пусть --- радикальная локальная формация. Если в конечной метанильпотентной группе существует -биектор 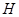, то 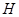является -холловской подгруппой группы .

 

Замечание. Группа не является метанильпотентной, но -проекторы и -инъекторы совпадают между собой и являются нехолловскими подгруппами порядка .

 

Теорема Пусть --- радикальный класс Шунка и --- нормально наследственный гомоморф. Если в каждой группе существует -биектор, то .

 

Доказательство. Предположим, что не содержится в , и пусть --- группа наименьшего порядка из разности . Если имеет простой порядок , то и , противоречие. Значит, --- группа непростого порядка и можно выбрать нетривиальную нормальную в подгруппу . Так как и --- -подгруппа в , то и .

Пусть --- -биектор в . Тогда --- -инъектор в и . Поскольку 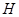является -проектором в , то -максимальна в . Так как --- гомоморф, то , а по выбору группы получаем, что , т. е. и , противоречие. Значит, допущение не верно и .

 

Следствие Если --- радикальный класс Шунка, для которого в каждой конечной разрешимой группе существует -биектор, то .

 

Следствие Если --- радикальная локальная формация, для которой в каждой конечной разрешимой группе существует -биектор, то .

Для натурального числа через обозначим класс всех разрешимых грeпп нильпотентной длины не более . При имеем класс всех нильпотентных групп, а при --- класс всех метанильпотентных групп.

 

Лемма Для любого натурального числа , класс является радикальной насыщенной наследственной формацией.

 

Доказательство. Применим индукцию по . При имеем класс всех нипьпотентных групп, он являетсяся насыщенной наследственной формацией и классом Фиттинга. Пусть утверждение справедливо для 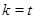. По следствию (3)

 

 

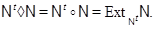
Но класс состоит из всех разрешимых групп нильпотентной длины, меньшей либо равной , т. е. , поэтому

 

 

Согласно следствию (2) класс 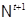насыщенная формация, а по теореме (1) и радикальныи. В силу леммы(1), он наследственныи класс. Следовательно, класс является радикальной насыщенной наследственной формацией. Лемма доказана.

 

Лемма Пусть --- разрешимая группа и . Если --- -проектор группы , то .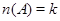

 

Доказательство. Поскольку --- насыщенная формация, то -проектор в группе существует согласно следствию. Поскольку 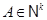, то . Если , то и утверждение доказано. Пусть и . По лемме(2), , а поскольку --- -проектор группы , то . Тогда , следовательно, , и