Лабораторная работа № 4
Определение длины световой волны с помощью бипризмы
Цель работы: определить длину световой волны из наблюдений интерференционной картины, получаемой с помощью бипризмы.
Краткаятеория
 Источники света называются когерентными, если они испускают волны одинаковой частоты и разность фаз колебаний этих волн не зависит от времени. Лучи света, испускаемые когерентными источниками, при наложении будут интерферировать, что приведет к возникновению светлых и темных участков во всей области наложения световых пучков - интерференционной картине. Результирующая интенсивность двух интерферирующих волн с интенсивностями I1 и I2 равна
Источники света называются когерентными, если они испускают волны одинаковой частоты и разность фаз колебаний этих волн не зависит от времени. Лучи света, испускаемые когерентными источниками, при наложении будут интерферировать, что приведет к возникновению светлых и темных участков во всей области наложения световых пучков - интерференционной картине. Результирующая интенсивность двух интерферирующих волн с интенсивностями I1 и I2 равна

 где
где 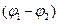 - разность фаз, которую имеют волны в точке наблюдения. Если разность фаз
- разность фаз, которую имеют волны в точке наблюдения. Если разность фаз  , где m - любое целое число, то результирующая интенсивность равна нулю (темные участки на интерференционной картине). При разности фаз
, где m - любое целое число, то результирующая интенсивность равна нулю (темные участки на интерференционной картине). При разности фаз 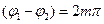 результирующая интенсивность максимальна (светлые участки на интерференционной картине).
результирующая интенсивность максимальна (светлые участки на интерференционной картине).
Разность фаз двух волн связана с их оптической разностью хода 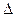 соотношением:
соотношением: 
где  - длина волны интерферирующих лучей. В точке M (рис.1) будет минимум освещенности, если волны от источников A и В придут в нее с разностью хода:
- длина волны интерферирующих лучей. В точке M (рис.1) будет минимум освещенности, если волны от источников A и В придут в нее с разностью хода:
 (1)
(1)
где n - показатель преломления среды, в которой распространяются волны. При разности хода:
 (2)
(2)
в точке М будет наблюдаться максимум освещенности.
Один из методов получения когерентных волн в оптике состоит в делении излучения, испускаемого точечным источником света, тем или иным способом на два потока, которые затем сводятся вместе в некоторой области пространства. В данной работе для разделения волн на два когерентных световых пучка используется бипризма.
Бипризма состоит из двух призм с малыми преломляющими углами (около 30’), сложенных одна с другой короткими сторонами (рис.2). Угол бипризмы (СОЕ), обращенный к источнику света близок к 1800. Источником света служит ярко освещенная узкая щель, установленная строго параллельно преломляющему ребру бипризмы. Вследствие преломления лучей верхняя половина бипризмы отклоняет падающий на нее пучок света вниз, а нижняя половина бипризмы – вверх. Таким образом, падающий пучок света разделяется бипризмой на два перекрывающихся пучка, как бы исходящих из двух мнимых изображений щели А и В.  Интерференционная картина, получающаяся при этом, соответствует интерференции света, исходящего из двух когерентных источников, расположенных в точках А и В и наблюдается в пространстве за бипризмой во всей
Интерференционная картина, получающаяся при этом, соответствует интерференции света, исходящего из двух когерентных источников, расположенных в точках А и В и наблюдается в пространстве за бипризмой во всей  области наложения световых пучков, испускаемых этими источниками. Так как все точки щели эквивалентны, то при монохроматическом свете источников А и В интерференционная; картина состоит из ряда светлых (максимумы) и темных (минимумы) полос, параллельных щели; ширина a светлых и темных полос одинакова. Светлая полоса, соответствующая разности фаз интерферирующих лучей
области наложения световых пучков, испускаемых этими источниками. Так как все точки щели эквивалентны, то при монохроматическом свете источников А и В интерференционная; картина состоит из ряда светлых (максимумы) и темных (минимумы) полос, параллельных щели; ширина a светлых и темных полос одинакова. Светлая полоса, соответствующая разности фаз интерферирующих лучей  , расположена в точке О (рис.1) и находится в центре интерференционной картины. Если источники А и В излучают белый свет, для каждой длины волны спектра получается своя система максимумов и минимумов.
, расположена в точке О (рис.1) и находится в центре интерференционной картины. Если источники А и В излучают белый свет, для каждой длины волны спектра получается своя система максимумов и минимумов.
Интерференционная картина при этом представляет собой чередующиеся цветные полосы, причем темных полос не будет нигде, т.к. места минимумов для одних длин волн совпадают с местами максимумов для других. Зная расстояние d между мнимыми источниками А и В, расстояние a между интерференционными полосами и расстояние D от щели до плоскости, в которой наблюдают интерференционную картину, можно определить длину волны света, испускаемого источниками.
Для вывода формулы, позволяющей определить длину волны с помощью бипризмы, рассмотрим два когерентных источника света, расположенных в точках А и В (рис.1). Расстояние d между источниками мало по сравнению с расстоянием D до плоскости, в которой наблюдают интерференционную картину. Определим разность хода волн, приходящих в точку М, расположенную на линии O’O’’ (O’O’’ ||АВ)на расстоянии x от точки О.
Из прямоугольных треугольников ANM и BKM и меем:


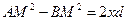

 , поскольку
, поскольку 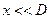 и
и  . Тогда
. Тогда


Расстояние светлой полосы с номером m от центральной, равное xm, найдем, используя условие максимума (2)  , откуда
, откуда  . Положение темных полос из условия минимума (1)
. Положение темных полос из условия минимума (1)  . Поскольку ширина светлых и темных полос одинакова, то расстояние между соседними светлыми или темными полосами равно:
. Поскольку ширина светлых и темных полос одинакова, то расстояние между соседними светлыми или темными полосами равно:
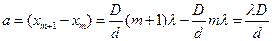
Тогда длина волны:  (4)
(4)
Описание установки

 Принципиальная оптическая схема установки для наблюдения интерференционной картины показана на рис.3. Здесь Л – источник света, Ф – светофильтр, пропускающий свет определенной длины волны, Щ – щель, БП – бипризма, ОМ – окулярный микрометр. Все элементы установки закрепляются в держателях и устанавливаются на оптической скамье. Щель освещается лампой накаливания и рассматривается как самостоятельный источник света. Ширина щели может изменяться с помощью двух винтов. При увеличении ширины щели увеличивается освещенность интерференционной картины, но уменьшается четкость интерференционных полос. При определенной ширине щели они совсем исчезают. Очевидно, что в этом случае источник света уже нельзя считать точечным. Монохроматический свет получают с помощью светофильтра Ф, помещенного между лампой Л и щелью Щ. Бипризма устанавливается на расстоянии 10 – 15 см от щели так, чтобы щель была строго параллельна ребру бипризмы (такая установка производится наклоном щели относительно ребра призмы с помощью бокового винта). С помощью окулярного микрометра ОМ, помещенного в область пересечения световых пучков, излучаемых мнимыми источниками света А и В (рис. 2), можно наблюдать интерференционную картину, а также измерять расстояние a между полосами интерференции и расстояние d между изображениями этих источников. Для измерения величины d надо в окулярном микрометре получить уменьшенное и увеличенное изображение источников А и В. Для этой цели на оптической скамье между бипризмой и окулярным микрометром устанавливают цилиндрическую линзу ЦЛ (рис.4). Передвигая линзу, добиваются, чтобы оба изображения были отчетливо видны в окуляре. В этом случае они лежат в той же плоскости, в которой наблюдалась интерференционная картина.
Принципиальная оптическая схема установки для наблюдения интерференционной картины показана на рис.3. Здесь Л – источник света, Ф – светофильтр, пропускающий свет определенной длины волны, Щ – щель, БП – бипризма, ОМ – окулярный микрометр. Все элементы установки закрепляются в держателях и устанавливаются на оптической скамье. Щель освещается лампой накаливания и рассматривается как самостоятельный источник света. Ширина щели может изменяться с помощью двух винтов. При увеличении ширины щели увеличивается освещенность интерференционной картины, но уменьшается четкость интерференционных полос. При определенной ширине щели они совсем исчезают. Очевидно, что в этом случае источник света уже нельзя считать точечным. Монохроматический свет получают с помощью светофильтра Ф, помещенного между лампой Л и щелью Щ. Бипризма устанавливается на расстоянии 10 – 15 см от щели так, чтобы щель была строго параллельна ребру бипризмы (такая установка производится наклоном щели относительно ребра призмы с помощью бокового винта). С помощью окулярного микрометра ОМ, помещенного в область пересечения световых пучков, излучаемых мнимыми источниками света А и В (рис. 2), можно наблюдать интерференционную картину, а также измерять расстояние a между полосами интерференции и расстояние d между изображениями этих источников. Для измерения величины d надо в окулярном микрометре получить уменьшенное и увеличенное изображение источников А и В. Для этой цели на оптической скамье между бипризмой и окулярным микрометром устанавливают цилиндрическую линзу ЦЛ (рис.4). Передвигая линзу, добиваются, чтобы оба изображения были отчетливо видны в окуляре. В этом случае они лежат в той же плоскости, в которой наблюдалась интерференционная картина.


Настройка установки
1. Бипризму помещают на расстоянии 10 – 15 см от щели так, чтобы ее преломляющие ребра были вертикальны. На расстоянии 30 – 50 см от бипризмы помещают окулярный микрометр. Лампу накаливания, середину щели, бипризму и окулярный микрометр устанавливают на одной высоте.
2. Включают лампу и добиваются равномерного освещения щели.
3. Сделав щель достаточно узкой, слегка поворачивают ее с помощью винтов около горизонтальной оси, добиваясь такого положения, чтобы щель была строго параллельна границе раздела призм в бипризме, а лучи света, проходящие через щель, попадали на границу раздела призм и в окулярный микрометр.
Границу раздела бипризм можно хорошо видеть при боковом положении глаза относительно призм, если приложить к призме кусок белой бумаги. В темной комнате хорошо видна невооруженным глазом проекция щели на входной линзе окулярного микрометра. Если проекция щели не попадает на окулярный микрометр, то его нужно сместить в горизонтальном направлении (с помощью винта).
Методикаизмерений
1. Измерение расстояния a между интерференционными полосами
Вращая микрометрический винт, устанавливают нулевое деление шкалы, видимой в окуляре (это деление играет роль метки), последовательно на середину двух любых достаточно удаленных друг от друга темных (или светлых) полос. Делают отсчеты n1 и nk положения середины этих полос по шкале окулярного микрометра и шкале микрометрического винта. Расстояние между двумя соседними светлыми (или темными) полосами
 (5)
(5)
где k – число светлых (или темных) полос, находящихся между взятыми первой и k-той полосой.
Измерения проделывают несколько раз, и результаты измерений записывают в таблицу. Цену деления шкалы окулярного микрометра можно найти, зная, что один оборот барабана окулярного микрометра соответствует перемещению окуляра по горизонтали на одно деление шкалы, т.е. на 0,5 мм.
2. Измерение расстояния d между двумя мнимыми источниками света
Для определения расстояния d получают (при помощи цилиндрической линзы) два изображения мнимых источников света А и В – уменьшенное и увеличенное. Линзу помещают между бипризмой и окуляром (рис.4). Передвигая линзу по скамье, находят два ее положения I и II, при которых в окуляре будут ясно видны изображения двух светящихся щелей равной интенсивности. Так как положение всех остальных приборов на оптической  скамье (щели, бипризмы и окуляра) должно оставаться неизменным (D = const), необходимо соблюдать условие D > 4F, где F – фокусное расстояние линзы. В используемой линзе F = 20 см, следовательно, D должно быть больше 80 см. Из построения хода лучей для I и II положения линзы (рис.5)
скамье (щели, бипризмы и окуляра) должно оставаться неизменным (D = const), необходимо соблюдать условие D > 4F, где F – фокусное расстояние линзы. В используемой линзе F = 20 см, следовательно, D должно быть больше 80 см. Из построения хода лучей для I и II положения линзы (рис.5)  видно, что положение I линзы дает увеличенное изображение источников света, а положение II – уменьшенное).
видно, что положение I линзы дает увеличенное изображение источников света, а положение II – уменьшенное).
Можно записать
 (для положения I линзы)
(для положения I линзы)
 (для положения II линзы)
(для положения II линзы)
где F – главное фокусное расстояние линзы, a1 и a2 – расстояние линзы от мнимых источников света, b1 и b2 – расстояния от линзы до фокальной плоскости окуляра. Вследствие обратимости лучей четкое изображение в положении II линзы получится в том случае, если расстояния a 1 = b 2, a 2 = b 1. Из подобия треугольников ACB и ECP следует, что
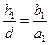 ,
,  (6)
(6)
где 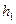 и
и  расстояния между изображениями источников света А и В, получаемыми с помощью линзы ЦЛ и наблюдаемыми в окуляре. Перемножая правые и левые части равенств (5), получаем
расстояния между изображениями источников света А и В, получаемыми с помощью линзы ЦЛ и наблюдаемыми в окуляре. Перемножая правые и левые части равенств (5), получаем

откуда  (7)
(7)
Измерения 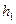 и
и  производятся с помощью окулярного микрометра несколько раз, результаты заносят в таблицу.
производятся с помощью окулярного микрометра несколько раз, результаты заносят в таблицу.
3. Измерение расстояния D от щели до окулярного микрометра
Величина D определяется как разность отсчетов (по шкале оптической скамьи), соответствующих положению щели и положению окуляра (измеряется один раз).
Обработка результатов эксперимента
По результатам измерений a, d, D по формуле (4) вычислите длину волны  , пропускаемую светофильтром, и оцените погрешности измерений.
, пропускаемую светофильтром, и оцените погрешности измерений.
Контрольные вопросы
1. Какие источники света называются когерентными? Какой метод получения когерентных источников света применяется в данной работе?
2. В чем состоит явление интерференции света?
3. Как определяется длина волны света при помощи бипризмы?
4. Как изменилось бы относительное расположение полос (минимумов и максимумов) на интерференционной картине при замене зеленого светофильтра на фиолетовый (красный)?
5. Почему максимумы и минимумы интенсивности на интерференционной картине имеют вид прямолинейных полос?