Расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны)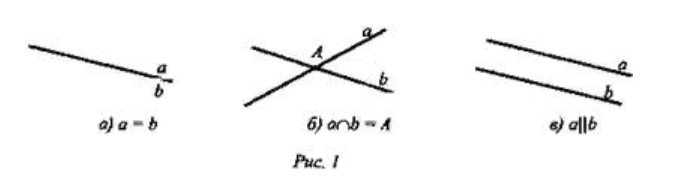 
Перейдем к взаимному расположению 2-х прямых в пространстве.
Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Но второй случай допускает две возможности: прямые лежат в одной плоскости (параллельны) или прямые не лежат в одной плоскости. В первом случае они параллельны, а во втором - такие прямые называются скрещивающимися.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Проиллюстрировать данные определения наглядно нам поможет куб.
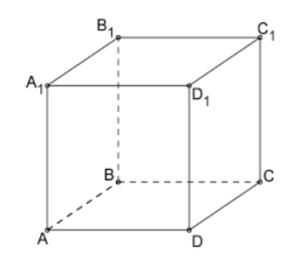
Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
- М и а задают плоскость α
- Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
- В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна - это нам известно из курса планиметрии.
- На чертеже эта прямая обозначена буквой b.
- Следовательно, b-единственная прямая, проходящая через точку М параллельно прямой а.
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.
Аналогично определяется параллельность отрезка и прямой, а так же параллельность двух лучей.
Лемма (это вспомогательная теорема, с помощью которой доказываются другие теоремы)Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
- Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
- Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)
3. Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей.
4. Прямые a, b и c находятся в плоскости β.
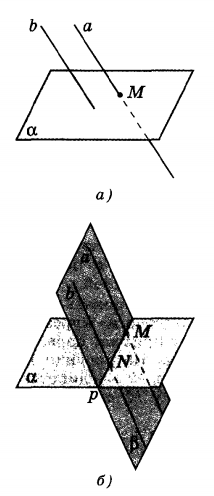
Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
Точку пересечения прямых a и p обозначим за N.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
Значит, прямая a пересекает плоскость α в точке N.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Дано: a∥c и b∥c
Доказать: a∥b
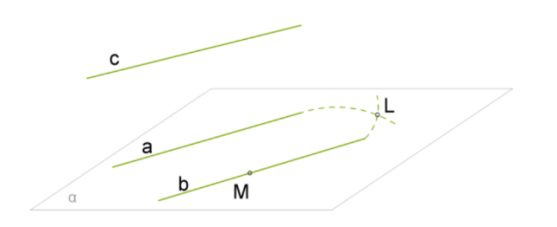
Доказательство:
Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Обозначение: a||α.
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка - она параллельна плоскости пола.
Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
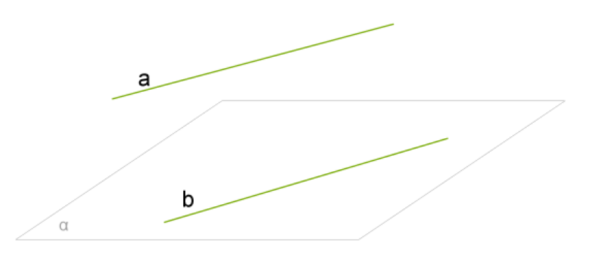
Доказательство:
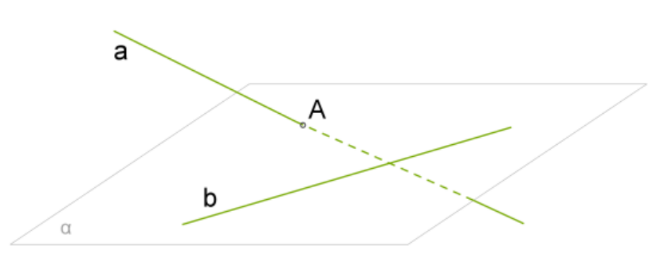
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.
Существует еще два утверждения, которые используются при решении задач:
1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.
Практическая работа.
Задача 1.
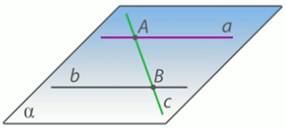
Параллельные прямые а и b лежат в плоскости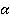 
. Докажите, что прямая с, пересекающая прямые а и b, также лежит в плоскости .
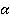Дано: а || b,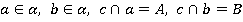 
Доказать: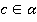 
Задача 2.
Средняя линия трапеции лежит в плоскости 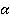, не совпадающей с плоскостью 
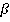. Пересекаются ли прямые, содержащие основания трапеции, с плоскостью ?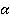