Тема. показатели вариации
1. Абсолютные показатели вариации.
2. Виды дисперсий и правило их сложения.
3. Дисперсия альтернативного признака.
4. Относительные показатели вариации.
Абсолютные показатели вариации
Для характеристики колеблемости признака в совокупности используются абсолютные и относительные показатели.
К абсолютным показателям вариации относят:
– размах вариации;
– среднее линейное (абсолютное) отклонение;
– дисперсия;
– среднее квадратическое отклонение.
Размах вариации – это разность между максимальным и минимальным значениями признака в совокупности:
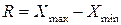
Размах вариации характеризует пределы изменения варьирующего признака.
Среднее линейное (абсолютное) отклонение определяется как средняя арифметическая из абсолютных отклонений (модулей) значений признака единиц совокупности от средней арифметической:
(1)
(2)
Дисперсия – средний квадрат отклонений индивидуальных значений признака от средней арифметической:
(1)
(2)
Пример. Распределение работников по среднемесячной заработной плате:
| Заработная плата, тыс. руб. | Число работников, чел. |
| До 12 | |
| 12–16 | |
| 16–20 | |
| 20–24 | |
| 24 и более | |
| Итого |
Определите дисперсию среднемесячной заработной платы.
Решение.
Таблица. Расчет дисперсии заработной платы
| Заработная плата, тыс. руб. | Число работников, чел. | 
| 
| 
| 
| 
|
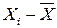
| До 12 | -7 | |||||
| 12–16 | -3 | |||||
| 16–20 | ||||||
| 20–24 | ||||||
| 24 и более | ||||||
| Итого | - | - | - |
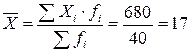
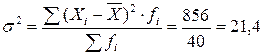
Для исчисления дисперсии также можно воспользоваться преобразованной (упрощенной) формулой:
|
|
,
т.е. дисперсия равна разности среднего квадрата значений признака и квадрата среднего значения признака:
где 
; 
.
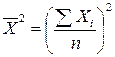Или если дисперсия взвешивается:
, 
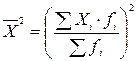
Таблица. Расчет дисперсии заработной платы по преобразованной формуле
| Заработная плата, тыс. руб. | Число работников, чел. |
|
| 
| 
|
| До 12 | |||||
| 12–16 | |||||
| 16–20 | |||||
| 20–24 | |||||
| 24 и более | |||||
| Итого | - |
.
Для рядов с равными интервалами можно применять способ отсчета от условного нуля (метод моментов). Для этого необходимо знать два свойства дисперсии:
Свойство 1. Если из всех значений вариант отнять постоянное число А, то дисперсия от этого не изменится:
.
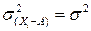Свойство 2. Если все значения вариант разделить на постоянное число h, то дисперсия уменьшится от этого в h2 раз. Обозначим 
, и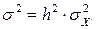 
Исчисление дисперсии способом отсчета от условного нуля сводится к следующим действиям:
1. Исходные варианты признака заменяют условными значениями 
.
2. Исчисляется дисперсия условной величины 
по формуле, аналогичной преобразованной формуле:
,
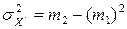где 
3. Исчисляем дисперсию величины 
по формуле: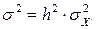
Таблица. Расчет дисперсии заработной платы
| Заработная плата, тыс. руб. | Число работников, чел. |
|
| 
| 
| 
|
| До 12 | -2 | -14 | ||||
| 12–16 | -1 | -9 | ||||
| 16–20 | ||||||
| 20–24 | ||||||
| 24 и более | ||||||
| Итого | - | -10 |
|
|
, 
, 
.
,
Среднее квадратическое отклонение (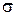
) представляет собой корень квадратный из дисперсии: 
Среднее квадратическое отклонение – величина именованная, имеет размерность усредняемого признака.
–2–
Вариация сгруппированных данных обычно оценивается дисперсией. В этом случае можно выделить три вида дисперсий: общая дисперсия, внутригрупповая дисперсия, межгрупповая дисперсия.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов:
,
где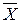 
– общая средняя для всей совокупности.
Внутригрупповая дисперсия измеряет вариацию признака внутри группы, которая возникает под влиянием не учитываемых факторов и не зависит от признака-фактора, положенного в основу группировки, и подсчитывается по формуле:
,
где 
– средняя по отдельным группам;
– численность единиц в отдельных группах.
Средняя из внутригрупповых дисперсий:
.
Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых средних вокруг общей средней и вычисляется:
.
Существует закон, связывающий три вида дисперсий – общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
.
Таким образом, общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
–3–
В статистике наряду с показателями вариации количественного признака определяются показатели вариации альтернативного признака, т.е. признака, которым единицы изучаемой совокупности могут либо обладать, либо не обладать. В таких случаях наличие признака обозначается 1, а его отсутствие – 0. Доля единиц, обладающих интересующим нас признаком, обозначается – p. Доля остальных единиц – q. При этом p + q = 1.
|
|
,
где m – количество единиц совокупности обладающих интересующим нас признаком;
n – всего единиц совокупности.
Определим для этих условий среднюю величину альтернативного признака:
.
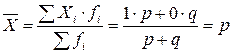Отсюда дисперсия альтернативного признака равна:
.
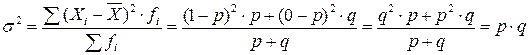Предельное значение дисперсии альтернативного признака равно 0,25. Оно получается при p = 0,5.
–4–
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительной вариации осуществляют как отношение абсолютного показателя вариации к средней арифметической (или медиане), умножаемое на 100%.
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:
.
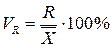2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
.
3. Коэффициент вариации характеризует относительную колеблемость значений признака вокруг средней величины:
.