Игра, элементы игры, классификация игр
Игра – конфликтная ситуация, участниками которой являются более, чем одна конкурирующая сторона.
Элементы игры:
· Игроки-участники игры
· Стратегии
· Целевая функция
Классификация игр:
1) По составу:
a) Коалиционные (возможно объединение)
b) Безкоалиционные (нельзя объединяться)
2) По количеству ходов:
a) Одношаговые
b) Многошаговые
3) По порядку ходов:
a) Одновременные
b) Последовательные
4) По непрерывности вариантов выбора:
a) Дискретные
b) Непрерывные
Формальное описание игры.
На консультации спрашивала Ожегова что он имел в виду под этим вопросом, он сказал следующее. Нужно написать классификацию (вопрос 1), написать, что в каждой игре должны быть заданы игроки (в т.ч. и их количество), последовательность ходов, совершенная или несовершенная информация, количество ходов в игре.
Совершенная информация – это игра, в которой в каждом узле игрок, который осуществляет выбор, знает в каком он узле и как он туда попал; ситуация, когда все информационные множества в дереве игры имеют не больше одного узла.
Несовершенная информация – это игра, в которой хотя бы в одном из узле игрок, который осуществляет выбор, не знает то, какое именно решение принял другой игрок; ситуация, когда информация не совершенна, то есть существует хотя бы одно информационное множество, в котором больше, чем 1 стратегия.
Доминирование.
Доминирование бывает 2 видов:
· Строгое
Si’ – доминируемая в Г

 ,
, 
Стратегия si доминирует стратегию si’, если значение целевой функции (выигрыш) i-того игрока при выборе стратегии si будет выше, чем при выборе si’ ,и будет больше, чем при любом выборе противника.
· Слабое
Si’ – слабодоминируемая в Г



 )
)

! 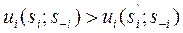
Стратегия si слабо доминирует стратегию si’, если значение целевой функции (выигрыш) i-того игрока при выборе стратегии si будет не меньше, и хотя бы 1 будет больше, чем при выборе si’ , и будет больше, чем при любом выборе противника.
P.S. Cистема обозначена восклицательным знаком (!) в слабодоминируемых стратегиях.
Общее знание»
ИГРА С ЧИСЛАМИ
ü Три игрока;
ü необходимо назвать 2/3 от среднего, которое назовут игроки.
Очевидно, что нет смысла называть числа большие чем 67, т.к. среднее арифметическое не может быть больше 100. Но, если все игроки рассуждают подобным образом, то все числа будут не больше чем 67 (то есть стратегия >67 доминируема в виду рациональности решения), значит и среднее арифметическое не превысит этого числа, а значит называть больше чем 2/3*67=45 (стратегия 67>=Si>45 – не доминируема в основной игре, но 0-67 также будет доминируема. Требует знания, что все ведут себя рационально и ты рационален). Повторяя данное рассуждение бесконечно много раз, придем к 1. Таким образом, решение рационально, вследствие «общего знания» о рациональности игроков.
“Общее знание” говорит: игра со всеми правилами известна игрокам и каждый из них знает, что все игроки осведомлены о том, что известно остальным партнерам по игре. И такое положение сохраняется до конца игры.
Лучший ответ»
1. Стратегия si* является лучшим ответом на конкретный выбор соперником s-i, если выполняется условие, при котором выигрыш от выбора стратегии si* будет не меньше выигрыша от выбора любой другой возможной стратегии si в ответ на конкретный выбор соперника s-i:
ui(si*; s-i)≥ ui(si; s-i), 
или
max(ui(si*; s-i)), 
или
si*=argmax(ui (si*; s-i)), 
2. Стратегия si* - лучший ответ на вероятность p выбора своих стратегий соперником, если выполняется следующее условие – ожидаемый выигрыш от стретегии i – ого игрока si* из матрицы распределения вероятностей не меньше, чем ожидаемый выигрыш при любом другом возможном выборе i – ого на действия соперника.
M[ui(si*; p)]≥ M[ui(si; p)], 
или
si – ло на max M[ui(si; p)], 
или
si = argmax M[ui (si*;p)], 

M[ui(si*; p)]= 
| Left | Right | |
| Up | 0/4 | 5/3 |
| Down | 3/5 | 6/6 |
ЛО1(L)=D ЛО1(R)= D ЛО2(U)=L ЛО1(D)= R
для смешанных стратегий:
p* - ло (в смешанных стратегиях), если конкретная рандомизация i – ого игрока pi*, принадлежащая равновесию Нэша, будет являться лучшим ответом i – ого игрока на действия соперника, который также будет играть РН:
pi*=ло(p-i*)
| Left | Right | |
| Up | 1/-1 | -1/1 |
| Down | -1/1 | 1/-1 |
P1=(½; ½)
p2=(½; ½)
Равновесие Нэша в чистых стратегиях
Вектор стратегий i-ого игрока Si*=<s1*,…,sn*> является равновесием Нэша, если Si* является лучшим ответом на действия соперника (S-i*), при  .
.
Si*=<s1*,…,sn*> - РН, еслиSi* - ЛО(S-i*), при  .
.
| L | C | R | |
| U | 0;4 | 4;0 | 5;3 |
| M | 4;0 | 0;4 | 5;3 |
| D | 3;5 | 3;5 | 6;6 |
Рассмотрим на примере:
Стратегия D первого игрока и стратегия R второго игрока (D,R) – равновесие Нэша в чистых стратегиях, так как ни у одного игрока не возникает строгого желания использовать другие свои стратегии, отсюда можно сделать вывод, что равновесие Нэша – пересечение лучших ответов соперников.
Смешанные стратегии
{pi(s1); pi(s2); …; pi(si)}
Pi – называется смешанной стратегией, если она является конкретной рандомизацией его чистых стратегий
p = <p1, p2, …, pn> - конкретная рандомизация для всех игроков
pi(si) – вероятность того, что i-тым игроком будет играться стратегия si
Σpi(si) = 1
*под суммой: si є Si *
Выигрыш i-того игрока от конкретной рандомизации «p» будет равен сумме выигрышей от его чистых стратегий, умноженных на вероятность того, что ИГРОК будет играть свою чистую стратегию.
Ui(p) = Σ(П pi(si))*ui(si)
*под суммой: s є S; над произведением: h; под произведением j=1*
РНСС
Лучший ответ для смешанных стратегий
Если какие-то стратегии входят в рандомизацию с ненулевой вероятностью и при этом смешанная стратегия является ЛО на какое-либо действие соперника, то si также является ЛО на какое-то действие.
*система*
pi(si)>0
si – тоже ЛО (s*-i)
РНСС
P* = <p*1, …, p*n> - РНСС, если:
P*i = ЛОi (p*-i) V i є n
Вектор p* будет являться РН в смешанных стратегиях, если конкретная рандомизация i-того игрока p*i, которая принадлежит равновесию Нэша, будет являться ЛО i-того игрока на действия соперников, которые также играют равновесие Нэша. Это верно для всех игроков.
S*i = ЛОi(p*-i)
Выводы по игре «Теннис » могут пригодиться и здесь:
1. С помощью РНСС можно предсказать пропорции людей, которые будут играть те или иные чистые стратегии;
2. Для проверки справедливости РНСС мы можем рассматривать уход игроков только в чистые стратегии;
3. Последствия от замены элементов в матрице выигрышей: замена элементов в матрице выигрышей у игрока, выигрыши которого стоят по строкам, влияет на распределение вероятностей игрока, выигрыши которого стоят по столбцам, и наоборот