Цель работы: исследование зависимости показателя преломления стекла от длины волны в области видимого излучения.
Приборы и принадлежности: стеклянная призма, гониометр, малогабаритный монохроматор.
Литература: [1], § 185-186; [2], § 46; [3], § 43-45; [4], § 6; [5], § 148.
В в е д е н и е
Дисперсией света называется зависимость фазовой скорости υ света в среде от его частоты ν или длины волны λ 0. Известно, что υ = c/n, где c – скорость света в вакууме, а n – показатель преломления среды. Поскольку c – универсальная постоянная, одинаковая для электромагнитных волн любой частоты, то существование дисперсии света в среде обусловлено тем, что ее показатель преломления n зависит от длины волны λ 0 (λ 0 – длина волны света в вакууме). Эта зависимость легко обнаруживается, например, при прохождении пучка белого света через призму, изготовленную из какого–либо прозрачного вещества. На экране, установленном за призмой, наблюдается радужная полоска, называемая призматическим, или дисперсионным спектром. Ярким проявлением дисперсии света в воде является замечательное природное явление – радуга.
Зависимость показателя преломления среды от длины электромагнитной волны в общем случае нелинейная и немонотонная. Области значений λ 0, в которых с ростом длины волны показатель преломления уменьшается, соответствуют нормальной дисперсии света. Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области длин волн наблюдается нормальная дисперсия.
Дисперсия света называется аномальной, если с ростом λ 0показатель преломления среды увеличивается. Аномальная дисперсия наблюдается в областях длин волн, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла эти полосы находятся в инфракрасной и ультрафиолетовой частях спектра.
В ХIХ веке выдающийся математик Коши теоретически рассчитал зависимость показателя преломления среды от длины волны λ 0. Он нашел, что эта зависимость может быть представлена в виде:
 , (1)
, (1)
где a, b, … - характерные для данного вещества постоянные. Для прозрачных стекол можно ограничиться двумя членами этого ряда. В таком случае
 . (2)
. (2)
Дисперсия света может быть объяснена на основе электромагнитной теории света и электронной теории вещества. При этом качественное объяснение состоит в следующем. Проходящая в среде электромагнитная волна возбуждает вынужденные колебания электронов, входящих в состав атомов вещества. Вынужденные колебания электронов сопровождаются излучением вторичных электромагнитных волн. Вторичные волны, складываясь с первичной, образуют результирующую волну. Из теории вынужденных механических колебаний следует, что фазы вторичных волн будут отличаться от фазы первичной волны. Это приводит к тому, что результирующая волна распространяется в веществе с фазовой скоростью, отличной от скорости волн в пустоте. Как известно, амплитуда вынужденных колебаний резко возрастает в условиях резонанса. Поэтому различие между υ и c будет тем больше, чемближе частота волны к собственной частоте колебаний электронов в атомах. Отсюда вытекает существование зависимости фазовой скорости волны в веществе от частоты ν или длины волны λ 0, т. е. дисперсия.
В данной работе дисперсия видимого света в стекле изучается с помощью призмы. Метод основан на измерении угла наименьшего отклонения лучей, прошедших через призму.
Монохроматический луч, падающий на боковую грань призмы под некоторым углом α, выходит из призмы отклоненным на угол γ (рис. 1). При этом угол γ является сложной функцией угла падения. Теоретический анализ хода лучей через призму показывает, что можно
 |
Рис. 1
найти такой угол падения луча на призму, при котором угол отклонения γ будет наименьшим. Луч внутри призмы проходит при этом параллельно основанию (рис. 1). Связь между углом наименьшего отклонения луча, прошедшего через призму, и показателем преломления вещества, из которого сделана призма, дается выражением
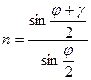 , (3)
, (3)
где φ – преломляющий угол призмы.
Измерив φ и γ, можно вычислить значения n для видимого излучения различной частоты ν (или длины волны λ 0) и найти, таким образом, зависимость n (ν) или n (λ 0).
Описание экспериментальной установки
Для измерения углов φ и γ используется гониометр, схема которого изображена на рис. 2. Гониометр состоит из зрительной трубы 1, коллиматора 2, столика 3, лимба 4, нониуса 5. Коллиматор служит для создания параллельного пучка света. Он состоит из наружного тубуса с объективом 6 и внутреннего тубуса с входной щелью 7, устанавливаемой в фокальной плоскости объектива.
 |
Рис. 2
Параллельный пучок света, вышедший из коллиматора, собирается объективом зрительной трубы в его фокальной плоскости, образуя действительное изображение щели, которое рассматривается через окуляр.
Если между коллиматором и зрительной трубой поставить призму, то для наблюдения изображения щели трубу необходимо будет повернуть относительно прежнего положения на некоторый угол, который можно измерить по шкале лимба с помощью нониуса. Призма помещается на столике 3, который может поворачиваться вокруг вертикальной оси, а также смещаться вдоль нее с помощью кремальеры.
Источником света в установке служит малогабаритный универсальный монохроматор. Оптическая схема монохроматора и его описание приведены в лабораторной работе № 8 «Дифракционная решетка».
Измерения и обработка результатов
Упражнение 1. Определение преломляющего угла призмы.
Для определения преломляющего угла призмы установите ее на столике гониометра так, чтобы биссектриса искомого угла φ совпадала с осью коллиматора (см. рис. 3).
 |
Пусть пучки, отраженные от двух граней призмы, образуют угол β. Легко показать, что β = 2 φ. Угол β определите, найдя разность двух отсчетов по шкале лимба, соответствующих двум положениям трубы, при которых видны изображения щели, образованные пучками ВА и СD.
Рис. 3
Вычислите преломляющий угол призмы φ.
Упражнение 2. Изучение зависимости показателя преломления стекла от длины световой волны.
Исследуйте зависимость показателя преломления стекла от λ 0 в интервале длин волн от 400 до 720 нм. Установите на монохроматоре длину волны 720 нм. Для определения угла наименьшего отклонения света столик с призмой поверните так, чтобы пучок, выходящий из коллиматора, падал на грань призмы под углом порядка 45˚ (рис. 4). Поворачивая зрительную трубу, найдите изображение щели. Изменяя угол падения лучей на входную грань призмы, добейтесь, чтобы это изображение максимально сместилось в сторону не отклоненного пучка (к оси коллиматора). Визирную нить, видимую в поле зрения трубы, наведите на изображение щели и сделайте соответствующий этому положению отсчет α 1по шкале лимба. Последовательно уменьшая длину волны на 40 нм в указанном выше интервале, найдите отсчеты α 1 при всех выбранных значениях длины волны. (Не забывайте при этом устанавливать призму в положение, соответствующее минимальному отклонения световых лучей, а также фокусировать окуляр зрительной трубы на изображение щели).
Для вычисления угла γпри определенной длине волны достаточно взять отсчет α 2, соответствующий не отклоненному пучку:
γ = | α 2 – α 1|.
 |
Показатель преломления n при каждом выбранном значении λ 0 вычислите по формуле (3).
Рис. 4
Результаты измерений и вычислений сведите в таблицу:
| φ | λ 0 | 1/ λ 02 | α 1 | α 2 | γ | n |
Постройте график зависимости показателя преломления стекла от длины волны света на координатной плоскости, показанной на рис. 6.
 |
Рис. 6
Дисперсия какого типа (нормальная или аномальная) наблюдается в исследованном интервале длин волн? В какой области спектра (длинноволновой или коротковолновой) зависимость n от λ 0 является более сильной?
Для проверки соответствия экспериментальных результатов формуле (2) постройте график зависимости показателя преломления стекла от 1/ λ 02. Если исследуемая зависимость является линейной в соответствии с формулой Коши, то определите по графику параметры a и b. Параметр a находится зкстраполяцией графика к значению 1/ λ 02, равному нулю.По наклону графика определяется постоянная b:
 .
.
Вычислите b в единицах нм2 и запишите в явном виде зависимость показателя преломления от длины волны, используя полученные значения параметров a и b.
Контрольные вопросы
1. Дайте определение абсолютного показателя преломления вещества.
2. В чем состоит явление дисперсии света? Приведите примеры наблюдения этого явления.
3. Опираясь на электронную теорию вещества, объясните качественно, почему фазовая скорость света в диэлектрике зависит от длины волны.
4. В каких случаях говорят об аномальной дисперсии?
5. Покажите, что φ = β /2 (см. рис. 3).