С помощью бипризмы Френеля

 

Цель работы: наблюдение явления интерференции света и экспериментальное измерение длины световой волны.

Приборы и принадлежности: оптическая скамья, бипризма, осветитель ОИ–19, щелевая диафрагма, окулярный микрометр, собирающая линза, светофильтры, метровая линейка.

Литература: [1], § 171 – 173; [2] § 51; [3], § 16 – 18;

[4], § 10 – 11; [5], § 139 – 140.

 

В в е д е н и е

 

Волновые свойства света наиболее ярко проявляются в явлении интерференции света, которое впервые наблюдал и описал итальянский физик Ф. Гримальди в XVII веке, а детально исследовал и объяснил французский физик Т. Юнг в 1802 г.

Явление интерференции света состоит в том, что при наложении двух или нескольких когерентных волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности.

Явление анализируется на основе принципа суперпозиции, которому подчиняются электрическое и магнитное поля. В соответствии с этим принципом, если в некоторой точке пространства происходит наложение электрических полей от двух источников, то напряженность результирующего поля

(1)

В случае сложения монохроматических волн, характеризующихся циклической частотой ω, векторы 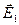и в некоторой точке пространства изменяются во времени по гармоническому закону:

 

(2)

. (3)

 

Напомним, что выражение ωt+φ=Ф под знаком косинуса называется фазой колебания φ – начальной фазой, а и - амплитудами слагаемых колебаний.

Согласно теории колебаний амплитуда результирующего колебания (при условии, что векторы и 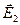лежат в одной плоскости) зависит от разности фаз слагаемых колебаний:

 

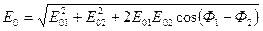(4)

 

Если разность фаз Ф ₁ - Ф ₂ слагаемых колебаний с течением времени не изменяется, то волны (и их источники) называются когерентными.

На практике реализуются такие условия, когда разности фаз слагаемых колебаний в разных точках пространства различны. В тех точках пространства, где разность фаз равна нулю или кратна 2π, амплитуда результирующего колебания, согласно (4), равна сумме амплитуд слагаемых колебаний:

 

Е₀=Е ₀₁ +Е ₀₂(5)

 

В соответствующих точках возникают максимумы интенсивности света. В тех же точках пространства, где разность Ф ₁ - Ф ₂ кратна нечетному числу π (в этом случае cos (Ф ₁- Ф ₂) = -1) амплитуда результирующего колебания

 

Е ₀ =| E ₀₁ –E ₀₂ |. (6)

 

В этих точках наблюдаются интерференционные минимумы.

Условия наблюдения максимумов и минимумов интенсивности света при интерференции волн от двух источников можно сформулировать иначе – через сравнение разности хода волн с длиной волны λ.

Рассмотрим, прежде всего, ситуацию, когда волны распространяются в однородной среде. В этом случае на всем пути распространения пучка света, длина волны λ остается неизменной. Рис. 1 моделирует ситуацию, когда в направлении оси Х распространяются волны от двух источников 1 и 2, находящихся в точках А и В. При этом разность хода волн Δr (отрезок АВ) равна длине волны. Очевидно, что при сложении эти волны будут усиливать друг друга; амплитуда результирующей волны будет равна сумме амплитуд слагаемых волн.

 

Рис. 1

 

Ситуация не изменится, если источник волн 2 перенести в точки А, С, D. Таким образом, интерференционный максимум наблюдается в том случае, когда разность хода волн равна нулю или кратна длине волны:

 

 

Δr = ± kλ (k = 0, 1, 2 …). (7)

 

Иная ситуация представлена на рис. 2. Разность хода волн здесь равна λ/2, в этом случае волны будут ослаблять друг друга. Аналогичное будет иметь место, если источник2 перенести в точку С , в точку D и т. д.

 

 

Рис. 2

 

Таким образом, минимум интенсивности света наблюдается в том случае, когда разность хода интерферирующих лучей кратна нечетному числу полуволн:

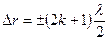(k = 0, 1, 2…). (8)

Если световые пучки на своем пути проходят через разные среды так, что длина волны не остается величиной постоянной, то для анализа явления интерференции вводятся понятия оптического пути и оптической разности хода. Оптический путь L луча в некоторой однородной среде равен произведению геометрического пути r на абсолютный показатель преломления среды n: L = rn. Если луч проходит через несколько слоев различных сред, то полный оптический путь равен сумме оптических путей в каждом слое. При этом результат интерференции двух световых пучков определяется соотношением между оптической разностью их хода Δ и длиной волны света в вакууме λ₀.

Условие интерференционного максимума:

 

Δ = ± kλ₀ (k = 0, 1, 2…). (9)

 

Условие интерференционного минимума:

(k = 0, 1, 2…). (10)

При наложении света от двух источников любого происхождения или даже от разных участков одного и того же источника интерференция не наблюдается. Следовательно, независимые источники света некогерентны. Причины этого заключены в самом механизме излучения света атомами (молекулами, ионами) источника света. Возбужденный атом излучает в течение очень короткого промежутка времени высвечивания τ ~10^-8 с, после чего он, растратив свою избыточную энергию на излучение, возвращается в нормальное (невозбужденное) состояние. Через некоторый промежуток времени атом может вновь возбудиться, получив энергию извне, и начать излучать. Такое прерывистое излучение света атомами в виде отдельных кратковременных импульсов – цугов волн – характерно для любого нелазерного источника света. В этом случае атомы излучают независимо друг от друга со случайными начальными фазами, беспорядочно изменяющимися от одного акта излучения атома к другому. Поэтому два источника света заведомо когерентными не являются.

Для получения когерентных световых волн применяют метод разделения света от одного источника на две волны или несколько волн. В каждой из них представлено излучение одних и тех же атомов источника, так что в силу общности происхождения эти системы волн когерентны между собой и интерферируют при наложении. Разделение света на когерентные системы волн можно осуществить путем его отражения и преломления, а также с помощью явления дифракции света.

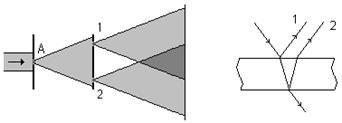Рис. 3 Рис. 4

 

В классическом эксперименте Юнга (рис. 3) получение когерентных волн 1 и 2 достигается расщеплением пучка света за счет дифракции при прохождении светом входной щели А. Другой способ наблюдения интерференции показан на рисунке 4. Здесь когерентные пучки света 1 и 2 получаются за счет отражения световой волны от передней и задней поверхностей пленки или пластинки.

Ниже рассматривается метод наблюдения интерференции света с помощью бипризмы Френеля.

Бипризма представляет собой две призмы с малыми преломляющими углами (порядка 30′), сложенные основаниями (рис. 5). Перед бипризмой устанавливается щелевая диафрагма, на которую направляется световой пучок от лампы накаливания. Дифракция света на щели приводит к образованию расходящегося пучка, падающего далее на бипризму. Таким образом, щель можно рассматривать как нитевидный источник света S. Чем уже щель, тем выше когерентность световых лучей, падающих на отдельные части бипризмы. Бипризма, преломляя световые пучки, обеспечивает их наложение. При этом перекрывающиеся пучки как бы исходят из двух мнимых изображений источника S₁ и S₂ (рис. 5). В пространстве за бипризмой наблюдается интерференционное поле, локализованное во всей области перекрытия пучков (при условии достаточно высокой монохроматичности излучения). На удаленном

Рис. 5

 

экране Э интерференционная картина представляет собой систему чередующихся светлых и темных полос.

Пусть d – расстояние между мнимыми источниками света, l – расстояние от них до экрана. Тогда в приближении l»d ширина интерференционной полосы (т.е. расстояние между соседними светлыми или темными полосами) определяется выражением:

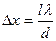. (11)

 

Описание экспериментальной установки

 

Оптическая схема экспериментальной установки представлена на рис. 6. На оптической скамье устанавливаются осветитель 1 со светофильтром, щелевая диафрагма 2 и бипризма 3. Ребро тупого угла

 

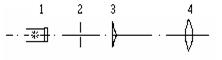
Рис. 6

 

бипризмы и щель должны быть расположены горизонтально, это облегчает дальнейшую настройку оптической системы. При этом следует позаботиться о том, чтобы ребро бипризмы было параллельно щели–источнику. Для этого смотрят сквозь бипризму на щель и, поворачивая оправу бипризмы вокруг горизонтальной оси, добиваются требуемой параллельности (должны быть видны две параллельные щели). Интерференционная картина наблюдается через окулярный микрометр 4, который устанавливается на расстоянии 30–50 см от бипризмы. (Положение плоскости наблюдения отмечено на окулярном микрометре специальной линией). Если картина недостаточно отчетлива, слегка поворачивают (не прекращая наблюдений!) оправу бипризмы; контраст картины также сильно зависит от ширины щели: малая ширина щели обеспечивает необходимую пространственную когерентность световых пучков, проходящих через обе части бипризмы.

Измерение ширины интерференционной полосы производится с помощью окулярного микрометра. В фокальной плоскости окуляра микрометра расположена неподвижная стеклянная пластинка со шкалой, каждое деление которой равно 1 мм. В этой же плоскости расположена вторая подвижная стеклянная пластинка с крестом и рисками Р (рис. 7).

Рис.7

 

Эта пластинка перемещается с помощью специального микрометрического винта. Шаг винта равен 1 мм. Таким образом, при повороте барабана винта на один оборот риски и крест в поле зрения окуляра перемещаются на одно деление неподвижной шкалы. Барабан винта разделен на 100 частей. Следовательно, цена деления шкалы барабана равна 0,01 мм. Полный отсчет по шкалам окулярного микрометра складывается из отсчета по неподвижной шкале и отсчета по барабану винта.

Внимание! При измерениях перемещать крест нитей окулярного микрометра следует очень осторожно, так как нажим на корпус микрометра может привести к сдвигу картины в поле зрения.

 

Измерения и обработка результатов

 

Упражнение 1. Наблюдение интерференционных картин.

Пронаблюдайте интерференционную картину в белом свете и опишите ее. Затем установите в световой пучок красный светофильтр. Опишите, какие принципиальные изменения произошли в интерференционной картине после установки светофильтра. Смените красный светофильтр на зеленый. Как (качественно) изменилась ширина наблюдаемых интерференционных полос?

Упражнение 2. Определение длины световой волны.

Производя наблюдение в лучах красного света, измерьте ширину интерференционной полосы. Для этого с помощью окулярного микрометра определите отрезок h, на котором укладывается определенное число (n =8–10) интерференционных полос. Отношение h/n дает ширину интерференционной полосы Δх

Определите расстояние d между мнимыми изображениями щели в бипризме. Для этой цели поместите на оптической скамье между бипризмой и микрометром собирающую линзу и, наблюдая через окулярный микрометр, добейтесь видимости изображений двух щелей. Измерьте расстояние d′ между ними. Затем с помощью линейки определите расстояние a от щели до линзы и расстояние b от линзы до плоскости наблюдения окулярного микрометра. В соответствии с формулой увеличения линзы искомое расстояние d найдется из соотношения d = (a/b)d′.

Измерьте расстояние l от щелевой диафрагмы до плоскости наблюдения окулярного микрометра и вычислите длину волны света по формуле

 

Измените положение бипризмы, сместив ее на 3-4 см вдоль оптической оси системы, и вновь произведите измерения и вычисления.

По результатам трех опытов найдите среднее значение длины волны; оцените погрешность Δλ ее измерения.

Результаты работы сведите в таблицу:

 

№	n	h	Δx	d′	a	b	d	l	λ	λ ср	Δλ

 

Контрольные вопросы

 

1. В чем состоит явление интерференции света, при каких условиях оно наблюдается?

2. Какие волны называются когерентными?

3. Что лежит в основе анализа явления интерференции света?

4. Можно ли получить интерференционную картину, используя в качестве источников света две одинаковые лампочки?

5. В чем состоит способ получения когерентных световых пучков? Как получают когерентные пучки при наблюдении интерференции с помощью бипризмы Френеля?

6. Сформулируйте условия возникновения максимумов и минимумов интенсивности света в интерференционной картине от двух источников.

7. Какой вид будет иметь интерференционная картина при освещении бипризмы белым светом?

Лабораторная работа № 5

Кольца Ньютона

Цель работы: наблюдение интерференционной картины колец Ньютона, экспериментальное определение радиуса кривизны линзы и длины световой волны.

Приборы и принадлежности: микроскоп МИ–1, система «линза-стеклянная пластинка» в оправе, осветитель ОИ-19, светофильтры.

Литература: [1], § 171 – 174; [2], § 53; [3], § 16 – 19; [4], § 10 – 11; [5], § 139 – 140.

В в е д е н и е*

Кольца Ньютона представляют собой интерференционную картину полос равной толщины, возникающей от воздушной прослойки между плоской стеклянной пластинкой и соприкасающейся с ней сферической линзой (рис.1). В этом случае геометрическим местом точек одинаковой толщины пленки является окружность, и поэтому соответствующие полосы равной толщины имеют вид концентрических окружностей с центром в точке соприкосновения линзы с пластинкой. Подобные полосы впервые наблюдались Гуком. Однако, вследствие того, что они были подробно изучены Ньютоном, их называют кольцами Ньютона.

Рис. 1

 

Кольца Ньютона можно наблюдать как в проходящем, так и в отраженном свете. Проведем расчет радиусов колец Ньютона, наблюдаемых в отраженном свете. В этом случае интерферировать будут лучи, отраженные от верхней и нижней границы воздушного зазора между линзой и пластинкой (лучи 1 и 2 на рис. 1).

Обычно лучи падают нормально к поверхности пластинки. Тогда, ввиду малой кривизны линзы, можно считать, что отражаются они также по нормали. В таком случае разность хода Δ лучей 1 и 2 на рис. 1 определяется удвоенной толщиной (d) воздушного зазора. Луч 2 отражается от оптически более плотной среды, фаза волны изменяется при этом на π, что эквивалентно дополнительной разности хода в половину длины волны. Таким образом,

Δ = 2d + (λ/2).

__________________

*См. также введение к лабораторной работе № 4.

Толщина воздушного зазора d зависит от расстояния r до точки соприкосновения линзы с пластинкой (рис. 2). Из треугольника АОС имеем:

 

r² = R² –(R–d)² = 2Rd – d².

 

Здесь R – радиус кривизны линзы, а λ – длина световой волны. С учетом неравенства R»d можно записать

 

r² = 2Rd, или d = r²/2R.

 

В точках, для которых выполняется условие

 

,

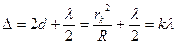Рис. 2

 

где k = 1, 2, 3,…, будут наблюдаться максимумы интенсивности отраженных лучей. Отсюда для радиуса светлого кольца с номером k имеем выражение:

 

. (1)

Наблюдению темных интерференционных колец соответствует условие Для радиуса темного кольца получим:

(2)

 

Измеряя радиусы колец при известной длине волны, можно по формулам (1) и (2) определить радиус кривизны линзы и обратно – по известному радиусу кривизны найти длину волны.

Отметим, что рассматриваемый метод наблюдения интерференции может быть применен для определения профилей и качества обработки поверхностей линз.

Формулы (1) и (2) справедливы, если в точке соприкосновения линза плотно прилегает к пластинке и их поверхности не деформированы. На практике, однако, добиться этого не удается, вследствие шероховатостей поверхностей, а также их деформаций. Как правило, преобладающим фактором является наличие деформаций линзы и пластинки в контактной области. В этом случае из оптической разности хода интерферирующих лучей следует вычесть удвоенную величину суммарной деформации t. В результате условие, определяющее радиус k -го темного кольца принимает вид:

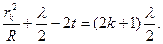(3)

 

Отсюда

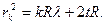(4)

 

Величина t не может быть измерена непосредственно, однако ее можно исключить. Для этого запишем выражение для квадрата радиуса темного кольца с номером m:

 

(5)

 

Вычитая из (5) выражение (4), получим

 

(6)

 

Отсюда

. (7)

 

Как правило, в ходе эксперимента измеряются не радиусы, а диаметры 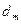и и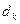нтерференционных колец. В таком случае целесообразно использовать расчетную формулу для R в виде:

 

. (8)