Затраты времени на осмотр больных

Таблица 4.1

Показатели роста (см.) 14 летних мальчиков

Рост, V (см.)	Число мальчиков, Р
Всего	n=17

 

В табл. 4.2 представлен пример сгруппированного вариационного ряда.

 

Таблица 4.2

Длительность лечения больных

 

Длительность лечения, день V	Число больных Р
3-5
6-8
9-11
Всего:	n=28

Средние величины – обобщающая характеристика признака в статистической совокупности.

Виды средних величин:

· мода (М_о);

· медиана (М_е),

· средняя арифметическая (М).

Свойство средней величины:

· занимает срединное положение;

· имеет абстрактный характер;

· сумма отклонений всех вариант от средней величины равна 0.

 

Мода – наиболее часто встречающаяся варианта в вариационном ряду.

Медиана – варианта, которая делит вариационный ряд на две равные части по числу наблюдения.

Из табл. 4.3 видно, что модой является число 143, поскольку число встречается чаще, чем другие Р = 6.

Таблица 4.3

Показатели роста мальчиков 14 лет

 

Рост, см V	Число мальчиков, Р
Всего	n=23

 

Средняя арифметическая имеет несколько методов вычисления.

Средняя арифметическая простая применяется, когда частота вариантов равна единице, т.е. каждая варианта встречается только один раз (Р=1).

Формула: 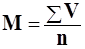где,

– сумма;

V – варианты;

n – число наблюдений.

Например, рост (см.) пяти больных: 166, 167, 168, 169, 170.

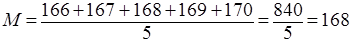см.

Средняя арифметическая взвешенная применяется, когда частота варианты встречаются по 2 и более раз (Р>1).

Формула: где

– сумма;

V – варианта;

Р – частота;

n – число наблюдений.

Таблица 4.4

Показатели роста подростков

Рост, см V	Число лиц Р	VР
Всего:	n=16	∑ 2687

 

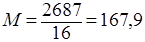см.

Для упрощения расчетов применяется средняя арифметическая взвешенная по способу моментов (см. специальную литературу).

Вычисление средней арифметической для сгруппированного вариационного ряда:

Для этого находят центральные варианты (середины интервала) как полусумму начального и конечного значения данного интервала. Далее расчет идет по формуле средней арифметической взвешенной.

Средняя геометрическая рассчитывается, когда количественный признак выражен дробными числами (табл.4.5).

Таблица 4.5

Затраты времени на осмотр больных

№ п/п	Время (час) V	Число больных Р
	0,2
	0,3
	0,5
	1,0
	Всего:	n=18

 

Формула: .

 

Критерии разнообразия признака в вариационном ряду:

Лимит – это отношение крайних значений вариационного ряда.

Формула: .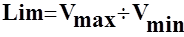

Например, вариационный ряд равен 166, 167, 168, 169, 170. 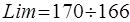=1,02

Амплитуда – это разница между крайними значениями вариационного ряда.

Формула: Отсюда .

 

Среднее квадратическое отклонение – сигма (σ) (см. тему №5).

Среднее квадратическое отклонение (сигма – σ) – характеризует рассеяние вариант (V) вокруг средней арифметической (М). Чем меньше значение σ, тем варианты плотнее концентрируются вокруг средней арифметической.

Аm – амплитуда,

К – коэффициент по размаху (см. приложение 3).

Коэффициент вариации (С_V) – это процентное отношение среднеквадратического отклонения (σ) к средней арифметической (М). Величина σ зависит от величины амплитуды ряда. Чем больше амплитуда, тем больше σ. Отсюда следует, что одинаковые средние величины могут иметь различные σ, их процентные отношения называются коэффициентом вариации. Формула вычисления коэффициента вариации: .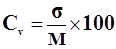

 

Принято считать:

· при 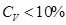– слабое разнообразие признака;

· при 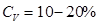– среднее разнообразие признака;

· при – сильное разнообразие признака.

Чем меньше разнообразие признака, тем варианты больше приближаются к среднему арифметическому.