Пусть 
и 
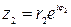, тогда:
1. Произведение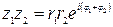 
;
2. Частное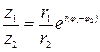 
;
3. Возведение в n – ю степень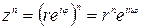 
;
4. Извлечение корня n – й степени 
, 
.
Формулы Эйлера.
Рассмотрим разложение функции 
по формуле Маклорена.
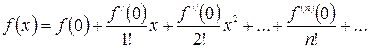
Если действительную переменную х заменить комплексной переменной z, то получим ряд по степеням z:
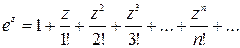(1)
Аналогично определяются тригонометрические функции 
и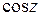 
комплексной переменной z:
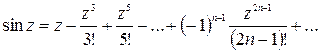(2)
(3)
Подставим в (1)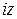 
вместо z и сгруппируем в правой части все слагаемые, содержащие множитель i и не содержащие этот множитель.
Сравнивая полученный результат с формулами (2) и (3), получаем
и 
Таким образом, с помощью понятия комплексного числа устанавливается связь между тригонометрическими и показательной функциями:
Складывая и вычитая эти два выражения, получим
; 
.
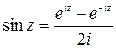Используя понятие комплексных чисел, вводится понятие гиперболических синуса и косинуса:
; 
.
Из формулы Эйлера следует, что
; 
.
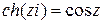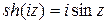Приведенные известные из элементарной математики формулы:
, 
;
; 
,
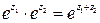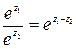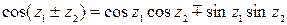справедливы и для комплексных значений аргументов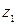 
и 
.
5. Основная теорема алгебры:
Функция вида 
, где п ‒ натуральное число,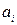 
‒ постоянные коэффициенты, называется многочленом п –ой степени с действительными коэффициентами (или целой рациональной функцией).
Корнем многочлена называется такое значение х 0 (вообще говоря комплексное) переменной х, при котором многочлен обращается в нуль.
Теорема: Если х 1 есть корень многочлена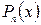 
, то многочлен делится без остатка на х‒х 1, т.е. 
, где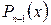 
‒ многочлен степени (п ‒1).
Теорема: (основная теорема алгебры) Всякий многочлен п -ой степени (n>0) имеет по крайней мере один корень, действительный или комплексный.
Теорема: Всякий многочлен 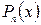можно представить в виде
,
где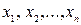 
‒ корни многочлена, 
‒ коэффициент многочлена при хп.
Множители 
называются линейными множителями.
Пример 1: Разложить многочлен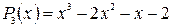 
на множители.
Решение: Многочлен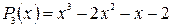 
обращается в нуль при 
Следовательно 
.
Пример 2: Представить выражение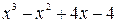 
в виде произведения линейных множителей.
Решение: Легко проверить, что 
является корнем данного многочлена.
= 
Уравнение 
имеет два комплексных корня 
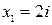и 
.
Следовательно, 
.
Если в разложении многочлена какой-либо корень встретился k раз, то он называется корнем кратности k. Тогда разложение многочлена можно записать в виде: 
, где 
‒ кратности соответственно корней 
.
Теорема: Если многочлен 
с действительными коэффициентами имеет комплексный корень 
, то он имеет сопряжённый корень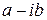 
.
Перемножив линейные множители,
,
получили трёхчлен второй степени с действительными коэффициентами
= 
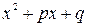, где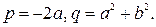 
Таким образом, произведение линейных множителей, соответствующих сопряжённым корням, можно заменить квадратным трёхчленом с действительными коэффициентами. Поэтому справедлива следующая теорема:
Теорема:
Всякий многочлен п- ой степени с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:
где 
,
х 1, х 2, …, хr ‒ корнимногочлена, а все квадратные трехчлены не имеют действительных корней.
Пример: 
этот многочлен имеет корни: х 1 = ‒ 2 и х 2 = 3, других действительных корней нет. Тогда 
.
Домашнее задание:
1. Выписать из текста определение и обозначение показательной формы комплексного числа.
2. Выписать правила действий над комплексными числами в показательной форме.
3. Дано: z1= 2 – 2i z2= 1 + i*√3. Записать эти числа в тригонометрической и показательной формах.
4. Выполнить любые три действия с z1 и z2 в показательной форме из упражнения 3.